Probabilistic Flux Limiters

The stable numerical integration of shocks in compressible flow simulations relies on the reduction or elimination of Gibbs phenomena (unstable, spurious oscillations). A popular method to virtually eliminate Gibbs oscillations caused by numerical discretization in under-resolved simulations is to use a flux limiter. A wide range of flux limiters has been studied in the literature, with recent interest in their optimization via machine learning methods trained on high-resolution datasets. The common use of flux limiters in numerical codes as plug-and-play blackbox components makes them key targets for design improvement. Moreover, while aleatoric (inherent randomness) and epistemic (lack of knowledge) uncertainty is commonplace in fluid dynamical systems, these effects are generally ignored in the design of flux limiters. Even for deterministic dynamical models, numerical uncertainty is introduced via coarse-graining required by insufficient computational power to solve all scales of motion. Here, we introduce a conceptually distinct type of flux limiter that is designed to handle the effects of randomness in the model and uncertainty in model parameters. This new, {\it probabilistic flux limiter}, learned with high-resolution data, consists of a set of flux limiting functions with associated probabilities, which define the frequencies of selection for their use. Using the example of Burgers' equation, we show that a machine learned, probabilistic flux limiter may be used in a shock capturing code to more accurately capture shock profiles. In particular, we show that our probabilistic flux limiter outperforms standard limiters, and can be successively improved upon (up to a point) by expanding the set of probabilistically chosen flux limiting functions.

Machine Learning for Detection of 3D Features using sparse X-ray data

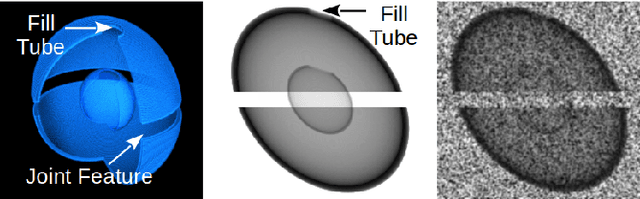
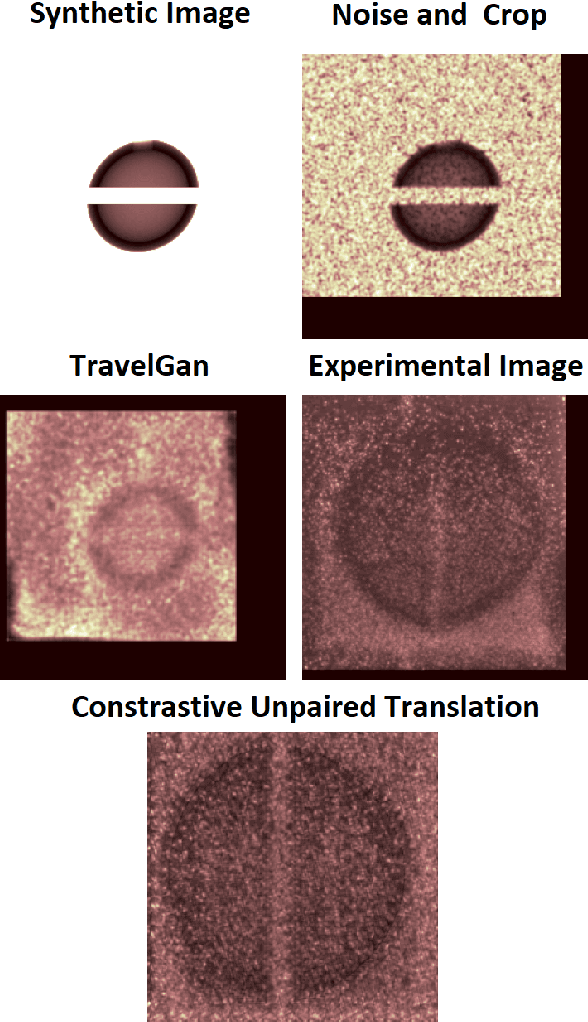
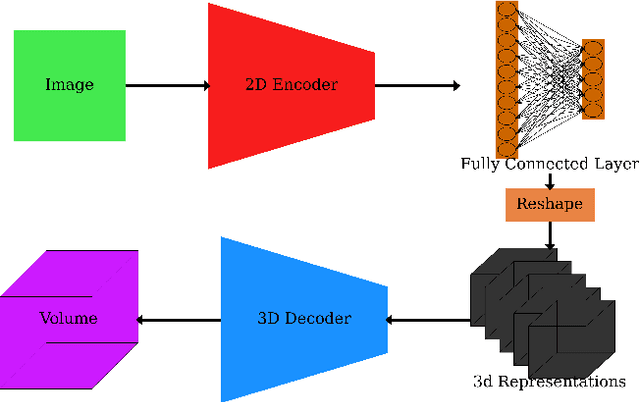
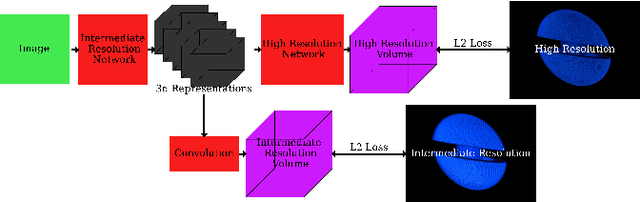
In many inertial confinement fusion experiments, the neutron yield and other parameters cannot be completely accounted for with one and two dimensional models. This discrepancy suggests that there are three dimensional effects which may be significant. Sources of these effects include defects in the shells and shell interfaces, the fill tube of the capsule, and the joint feature in double shell targets. Due to their ability to penetrate materials, X-rays are used to capture the internal structure of objects. Methods such as Computational Tomography use X-ray radiographs from hundreds of projections in order to reconstruct a three dimensional model of the object. In experimental environments, such as the National Ignition Facility and Omega-60, the availability of these views is scarce and in many cases only consist of a single line of sight. Mathematical reconstruction of a 3D object from sparse views is an ill-posed inverse problem. These types of problems are typically solved by utilizing prior information. Neural networks have been used for the task of 3D reconstruction as they are capable of encoding and leveraging this prior information. We utilize half a dozen different convolutional neural networks to produce different 3D representations of ICF implosions from the experimental data. We utilize deep supervision to train a neural network to produce high resolution reconstructions. We use these representations to track 3D features of the capsules such as the ablator, inner shell, and the joint between shell hemispheres. Machine learning, supplemented by different priors, is a promising method for 3D reconstructions in ICF and X-ray radiography in general.