Michael McKerns
Probabilistic Flux Limiters
May 13, 2024



Abstract:The stable numerical integration of shocks in compressible flow simulations relies on the reduction or elimination of Gibbs phenomena (unstable, spurious oscillations). A popular method to virtually eliminate Gibbs oscillations caused by numerical discretization in under-resolved simulations is to use a flux limiter. A wide range of flux limiters has been studied in the literature, with recent interest in their optimization via machine learning methods trained on high-resolution datasets. The common use of flux limiters in numerical codes as plug-and-play blackbox components makes them key targets for design improvement. Moreover, while aleatoric (inherent randomness) and epistemic (lack of knowledge) uncertainty is commonplace in fluid dynamical systems, these effects are generally ignored in the design of flux limiters. Even for deterministic dynamical models, numerical uncertainty is introduced via coarse-graining required by insufficient computational power to solve all scales of motion. Here, we introduce a conceptually distinct type of flux limiter that is designed to handle the effects of randomness in the model and uncertainty in model parameters. This new, {\it probabilistic flux limiter}, learned with high-resolution data, consists of a set of flux limiting functions with associated probabilities, which define the frequencies of selection for their use. Using the example of Burgers' equation, we show that a machine learned, probabilistic flux limiter may be used in a shock capturing code to more accurately capture shock profiles. In particular, we show that our probabilistic flux limiter outperforms standard limiters, and can be successively improved upon (up to a point) by expanding the set of probabilistically chosen flux limiting functions.
Predictive Scale-Bridging Simulations through Active Learning
Sep 20, 2022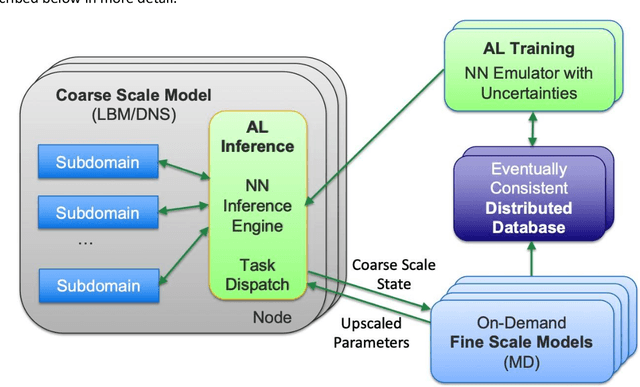
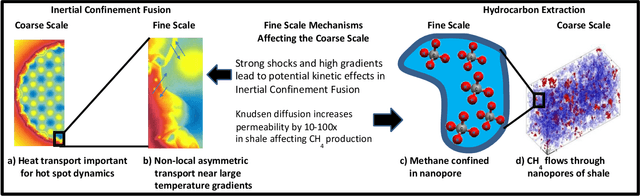
Abstract:Throughout computational science, there is a growing need to utilize the continual improvements in raw computational horsepower to achieve greater physical fidelity through scale-bridging over brute-force increases in the number of mesh elements. For instance, quantitative predictions of transport in nanoporous media, critical to hydrocarbon extraction from tight shale formations, are impossible without accounting for molecular-level interactions. Similarly, inertial confinement fusion simulations rely on numerical diffusion to simulate molecular effects such as non-local transport and mixing without truly accounting for molecular interactions. With these two disparate applications in mind, we develop a novel capability which uses an active learning approach to optimize the use of local fine-scale simulations for informing coarse-scale hydrodynamics. Our approach addresses three challenges: forecasting continuum coarse-scale trajectory to speculatively execute new fine-scale molecular dynamics calculations, dynamically updating coarse-scale from fine-scale calculations, and quantifying uncertainty in neural network models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge