The Backpropagation Algorithm Implemented on Spiking Neuromorphic Hardware

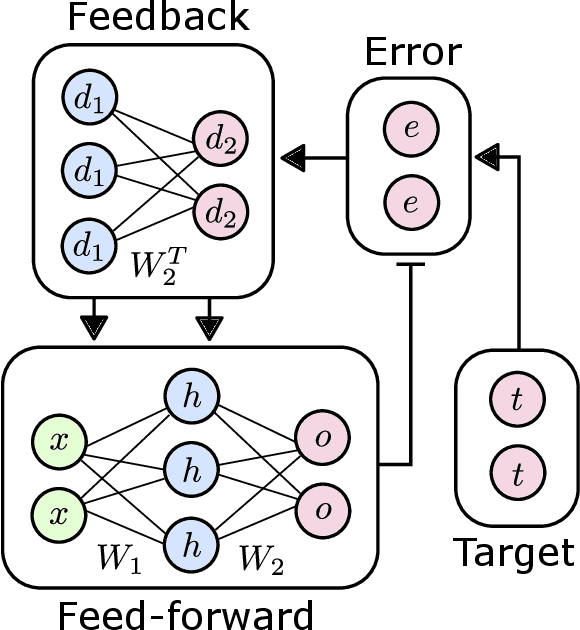
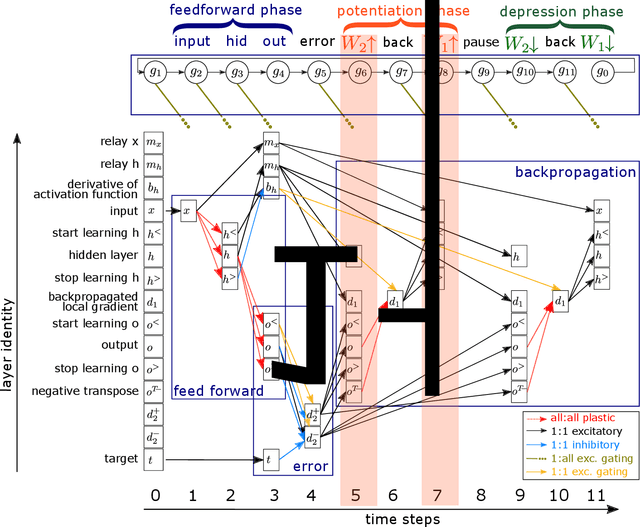
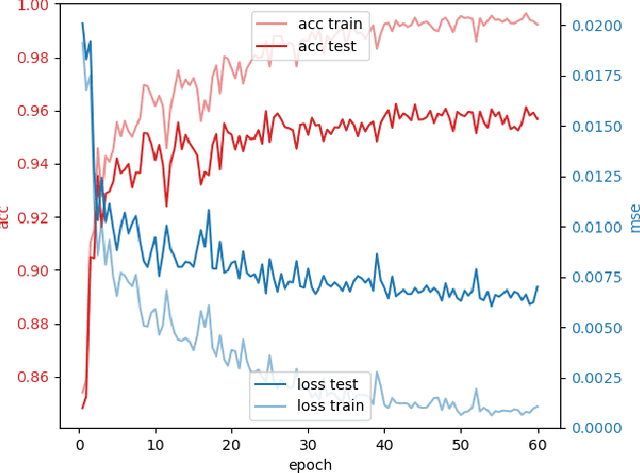
The capabilities of natural neural systems have inspired new generations of machine learning algorithms as well as neuromorphic very large-scale integrated (VLSI) circuits capable of fast, low-power information processing. However, most modern machine learning algorithms are not neurophysiologically plausible and thus are not directly implementable in neuromorphic hardware. In particular, the workhorse of modern deep learning, the backpropagation algorithm, has proven difficult to translate to neuromorphic hardware. In this study, we present a neuromorphic, spiking backpropagation algorithm based on pulse-gated dynamical information coordination and processing, implemented on Intel's Loihi neuromorphic research processor. We demonstrate a proof-of-principle three-layer circuit that learns to classify digits from the MNIST dataset. This implementation shows a path for using massively parallel, low-power, low-latency neuromorphic processors in modern deep learning applications.

Evidence of an exponential speed-up in the solution of hard optimization problems

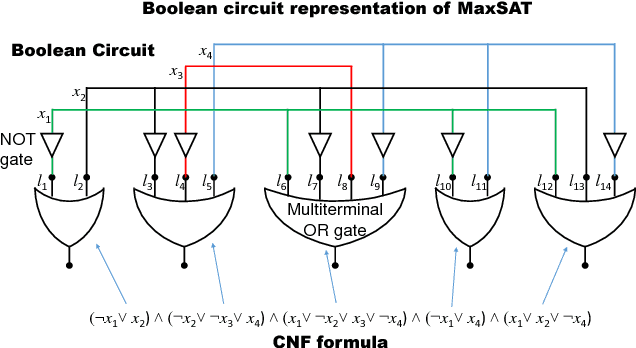
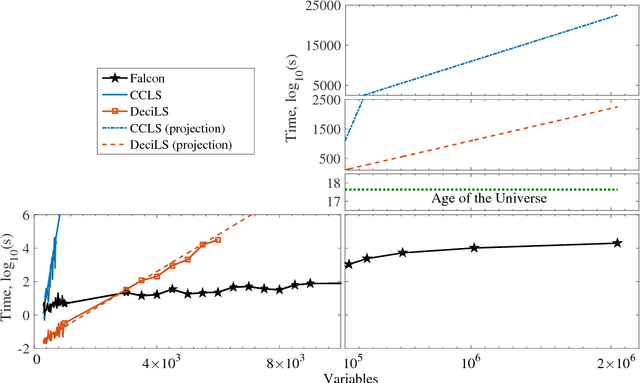
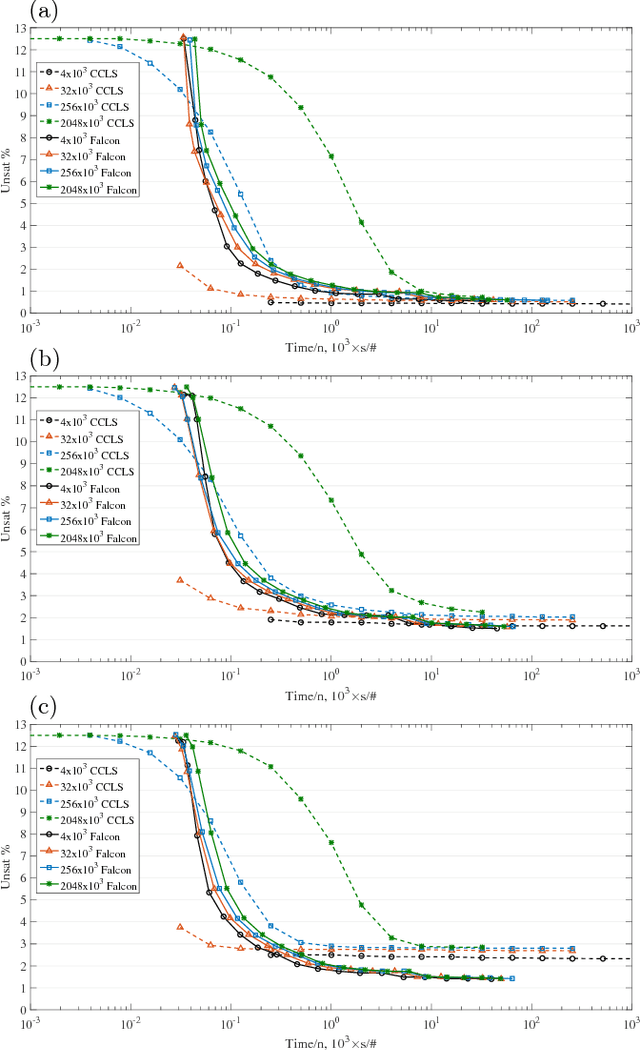
Optimization problems pervade essentially every scientific discipline and industry. Many such problems require finding a solution that maximizes the number of constraints satisfied. Often, these problems are particularly difficult to solve because they belong to the NP-hard class, namely algorithms that always find a solution in polynomial time are not known. Over the past decades, research has focused on developing heuristic approaches that attempt to find an approximation to the solution. However, despite numerous research efforts, in many cases even approximations to the optimal solution are hard to find, as the computational time for further refining a candidate solution grows exponentially with input size. Here, we show a non-combinatorial approach to hard optimization problems that achieves an exponential speed-up and finds better approximations than the current state-of-the-art. First, we map the optimization problem into a boolean circuit made of specially designed, self-organizing logic gates, which can be built with (non-quantum) electronic components; the equilibrium points of the circuit represent the approximation to the problem at hand. Then, we solve its associated non-linear ordinary differential equations numerically, towards the equilibrium points. We demonstrate this exponential gain by comparing a sequential MatLab implementation of our solver with the winners of the 2016 Max-SAT competition on a variety of hard optimization instances. We show empirical evidence that our solver scales linearly with the size of the problem, both in time and memory, and argue that this property derives from the collective behavior of the simulated physical circuit. Our approach can be applied to other types of optimization problems and the results presented here have far-reaching consequences in many fields.