Massimiliano Di Ventra
A Generative Neural Annealer for Black-Box Combinatorial Optimization
May 14, 2025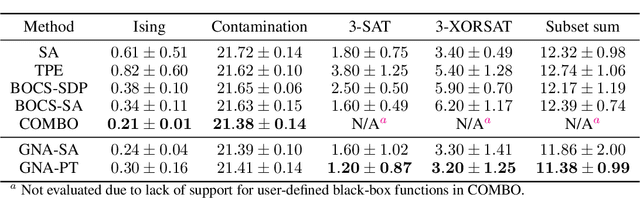
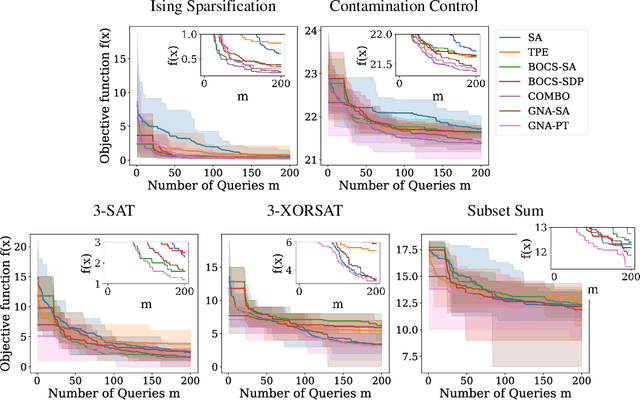
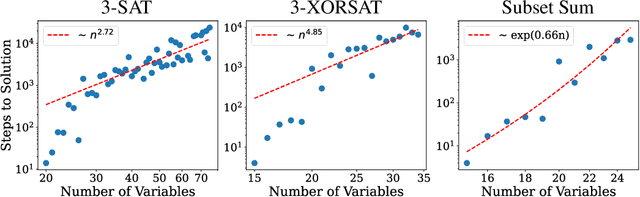
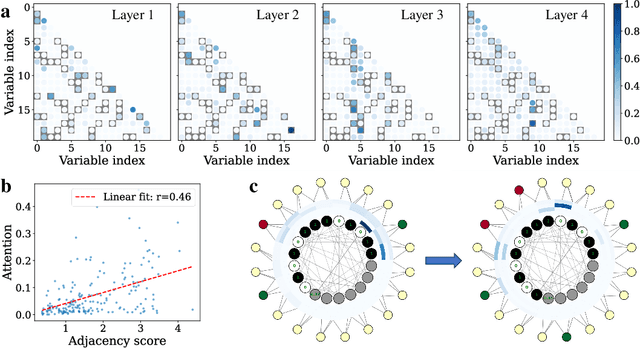
Abstract:We propose a generative, end-to-end solver for black-box combinatorial optimization that emphasizes both sample efficiency and solution quality on NP problems. Drawing inspiration from annealing-based algorithms, we treat the black-box objective as an energy function and train a neural network to model the associated Boltzmann distribution. By conditioning on temperature, the network captures a continuum of distributions--from near-uniform at high temperatures to sharply peaked around global optima at low temperatures--thereby learning the structure of the energy landscape and facilitating global optimization. When queries are expensive, the temperature-dependent distributions naturally enable data augmentation and improve sample efficiency. When queries are cheap but the problem remains hard, the model learns implicit variable interactions, effectively "opening" the black box. We validate our approach on challenging combinatorial tasks under both limited and unlimited query budgets, showing competitive performance against state-of-the-art black-box optimizers.
Implementation of digital MemComputing using standard electronic components
Oct 03, 2023



Abstract:Digital MemComputing machines (DMMs), which employ nonlinear dynamical systems with memory (time non-locality), have proven to be a robust and scalable unconventional computing approach for solving a wide variety of combinatorial optimization problems. However, most of the research so far has focused on the numerical simulations of the equations of motion of DMMs. This inevitably subjects time to discretization, which brings its own (numerical) issues that would be absent in actual physical systems operating in continuous time. Although hardware realizations of DMMs have been previously suggested, their implementation would require materials and devices that are not so easy to integrate with traditional electronics. In this study, we propose a novel hardware design for DMMs that leverages only conventional electronic components. Our findings suggest that this design offers a marked improvement in speed compared to existing realizations of these machines, without requiring special materials or novel device concepts. We also show that these DMMs are robust against additive noise. Moreover, the absence of numerical noise promises enhanced stability over extended periods of the machines' operation, paving the way for addressing even more complex problems.
Self-Averaging of Digital MemComputing Machines
Jan 20, 2023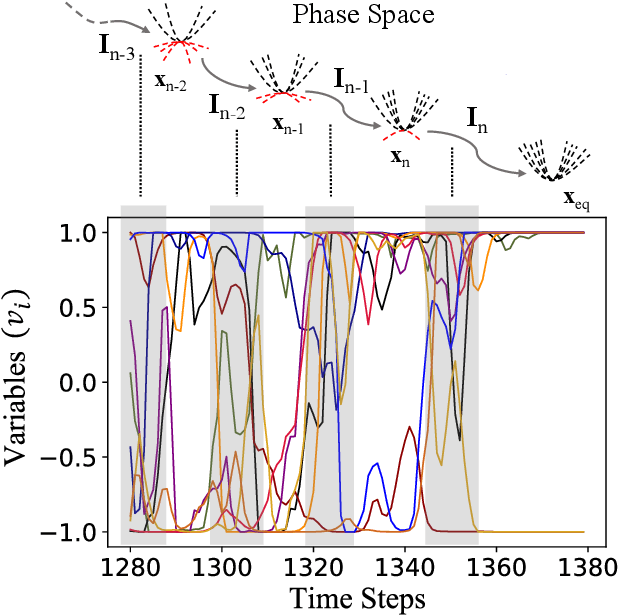
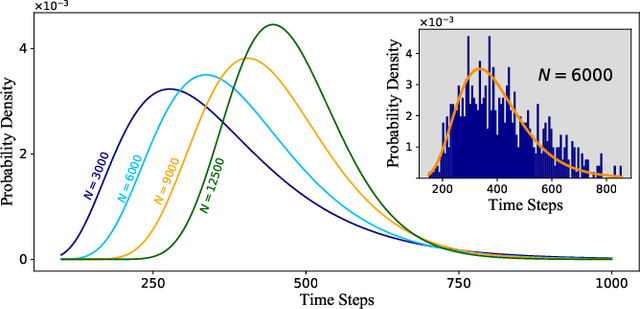
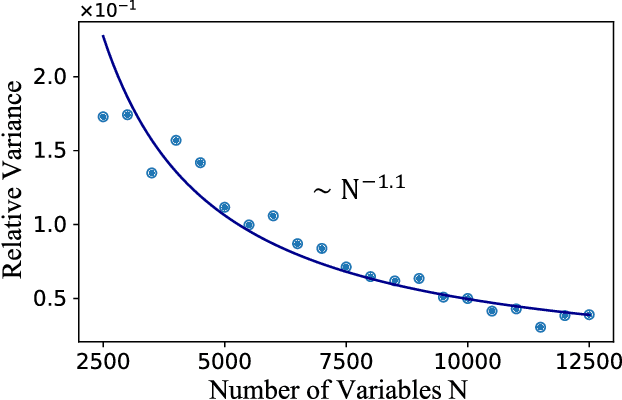
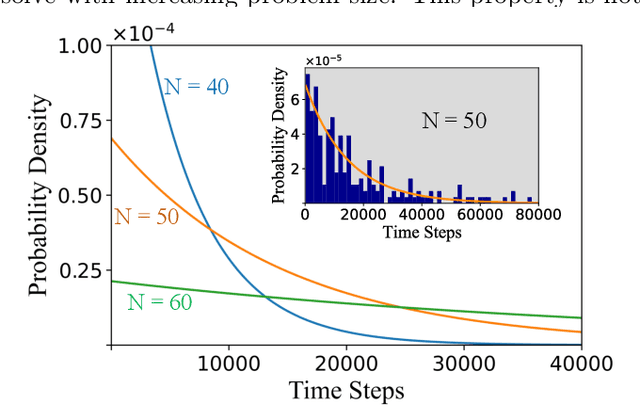
Abstract:Digital MemComputing machines (DMMs) are a new class of computing machines that employ non-quantum dynamical systems with memory to solve combinatorial optimization problems. Here, we show that the time to solution (TTS) of DMMs follows an inverse Gaussian distribution, with the TTS self-averaging with increasing problem size, irrespective of the problem they solve. We provide both an analytical understanding of this phenomenon and numerical evidence by solving instances of the 3-SAT (satisfiability) problem. The self-averaging property of DMMs with problem size implies that they are increasingly insensitive to the detailed features of the instances they solve. This is in sharp contrast to traditional algorithms applied to the same problems, illustrating another advantage of this physics-based approach to computation.
Mode-Assisted Joint Training of Deep Boltzmann Machines
Feb 17, 2021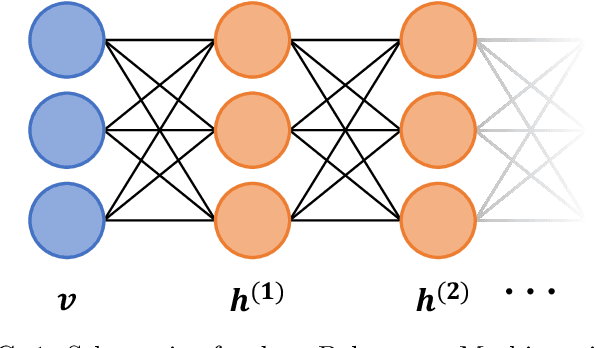
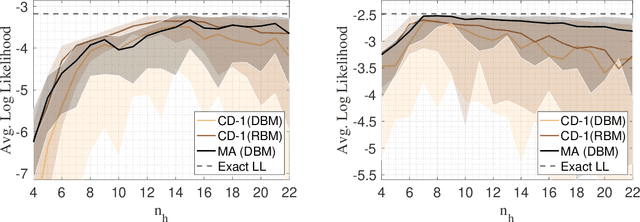
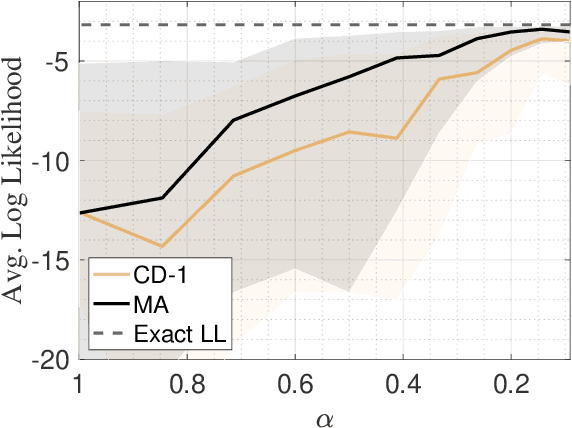
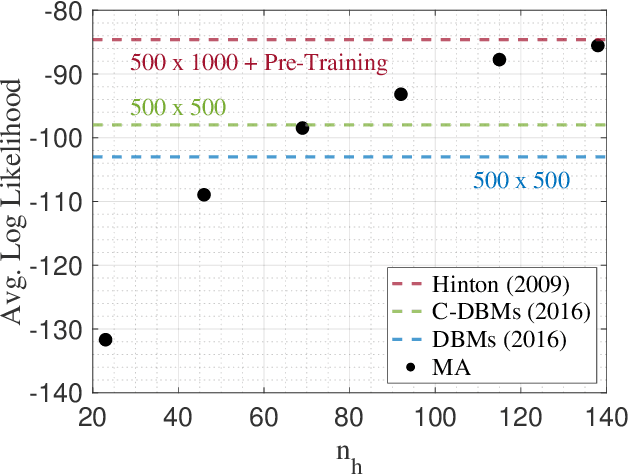
Abstract:The deep extension of the restricted Boltzmann machine (RBM), known as the deep Boltzmann machine (DBM), is an expressive family of machine learning models which can serve as compact representations of complex probability distributions. However, jointly training DBMs in the unsupervised setting has proven to be a formidable task. A recent technique we have proposed, called mode-assisted training, has shown great success in improving the unsupervised training of RBMs. Here, we show that the performance gains of the mode-assisted training are even more dramatic for DBMs. In fact, DBMs jointly trained with the mode-assisted algorithm can represent the same data set with orders of magnitude lower number of total parameters compared to state-of-the-art training procedures and even with respect to RBMs, provided a fan-in network topology is also introduced. This substantial saving in number of parameters makes this training method very appealing also for hardware implementations.
Directed percolation and numerical stability of simulations of digital memcomputing machines
Feb 06, 2021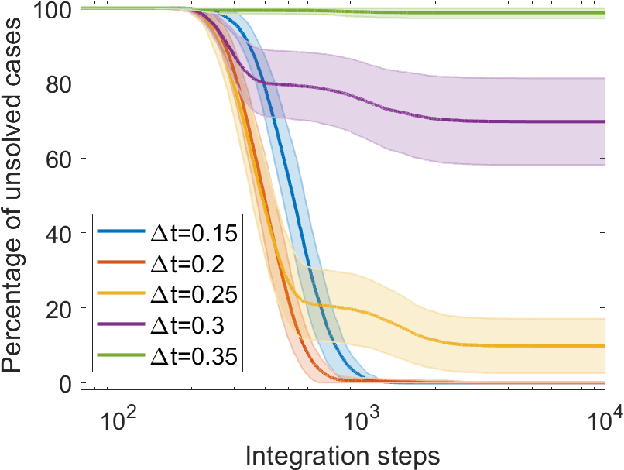
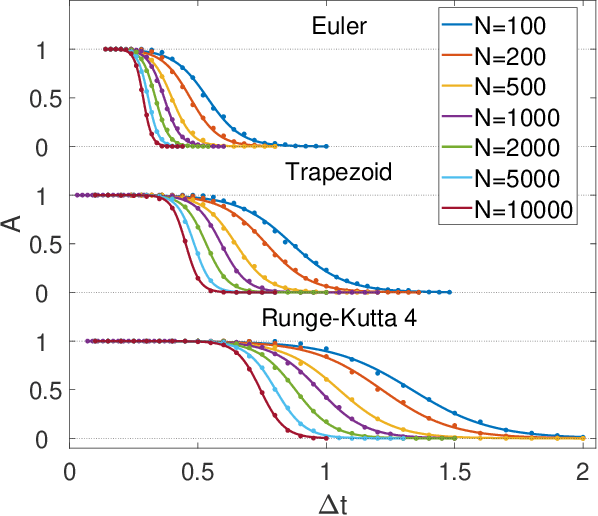
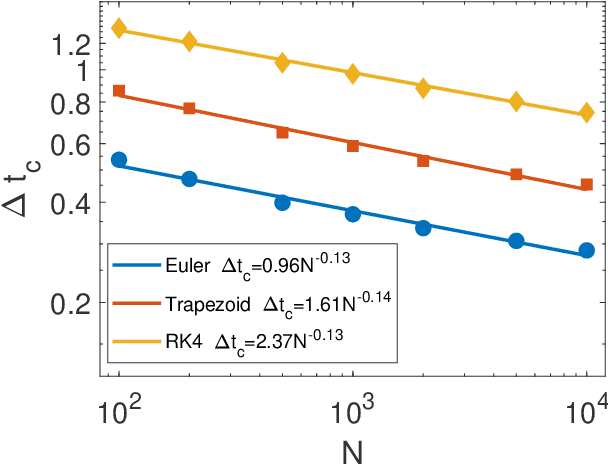
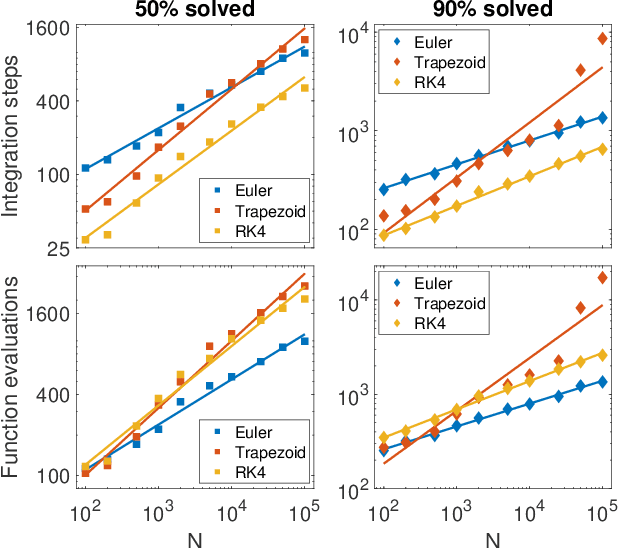
Abstract:Digital memcomputing machines (DMMs) are a novel, non-Turing class of machines designed to solve combinatorial optimization problems. They can be physically realized with continuous-time, non-quantum dynamical systems with memory (time non-locality), whose ordinary differential equations (ODEs) can be numerically integrated on modern computers. Solutions of many hard problems have been reported by numerically integrating the ODEs of DMMs, showing substantial advantages over state-of-the-art solvers. To investigate the reasons behind the robustness and effectiveness of this method, we employ three explicit integration schemes (forward Euler, trapezoid and Runge-Kutta 4th order) with a constant time step, to solve 3-SAT instances with planted solutions. We show that, (i) even if most of the trajectories in the phase space are destroyed by numerical noise, the solution can still be achieved; (ii) the forward Euler method, although having the largest numerical error, solves the instances in the least amount of function evaluations; and (iii) when increasing the integration time step, the system undergoes a "solvable-unsolvable transition" at a critical threshold, which needs to decay at most as a power law with the problem size, to control the numerical errors. To explain these results, we model the dynamical behavior of DMMs as directed percolation of the state trajectory in the phase space in the presence of noise. This viewpoint clarifies the reasons behind their numerical robustness and provides an analytical understanding of the unsolvable-solvable transition. These results land further support to the usefulness of DMMs in the solution of hard combinatorial optimization problems.
Mode-Assisted Unsupervised Learning of Restricted Boltzmann Machines
Jan 19, 2020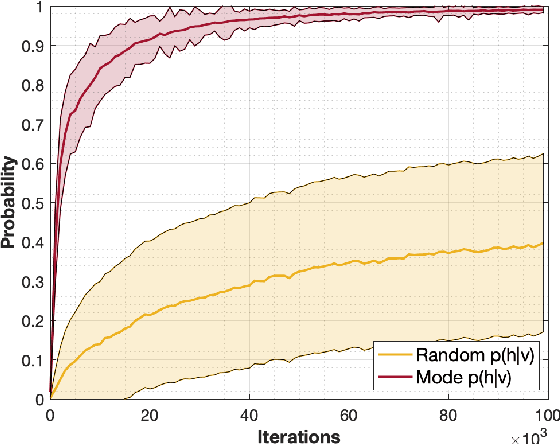
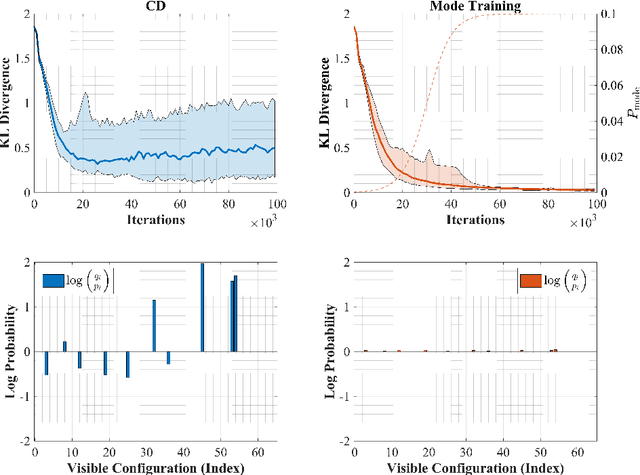
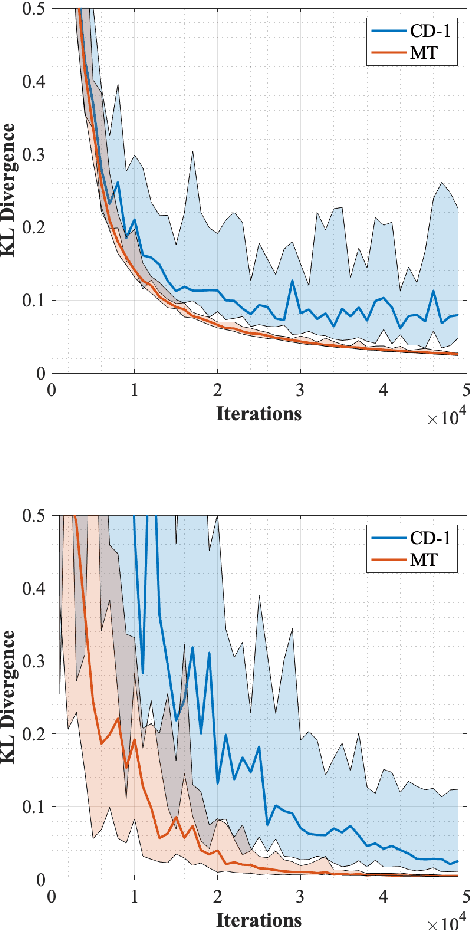
Abstract:Restricted Boltzmann machines (RBMs) are a powerful class of generative models, but their training requires computing a gradient that, unlike supervised backpropagation on typical loss functions, is notoriously difficult even to approximate. Here, we show that properly combining standard gradient updates with an off-gradient direction, constructed from samples of the RBM ground state (mode), improves their training dramatically over traditional gradient methods. This approach, which we call mode training, promotes faster training and stability, in addition to lower converged relative entropy (KL divergence). Along with the proofs of stability and convergence of this method, we also demonstrate its efficacy on synthetic datasets where we can compute KL divergences exactly, as well as on a larger machine learning standard, MNIST. The mode training we suggest is quite versatile, as it can be applied in conjunction with any given gradient method, and is easily extended to more general energy-based neural network structures such as deep, convolutional and unrestricted Boltzmann machines.
Generating Weighted MAX-2-SAT Instances of Tunable Difficulty with Frustrated Loops
May 14, 2019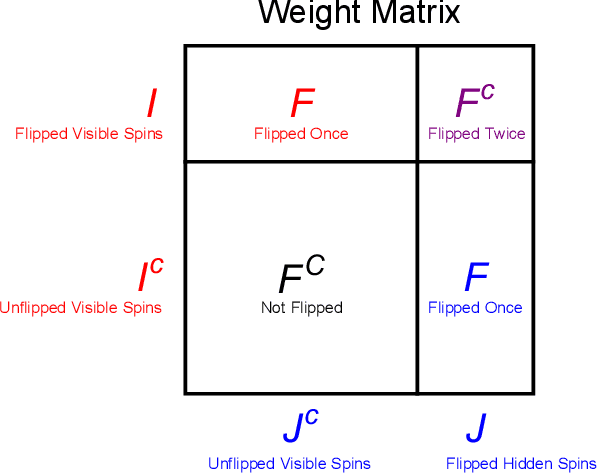

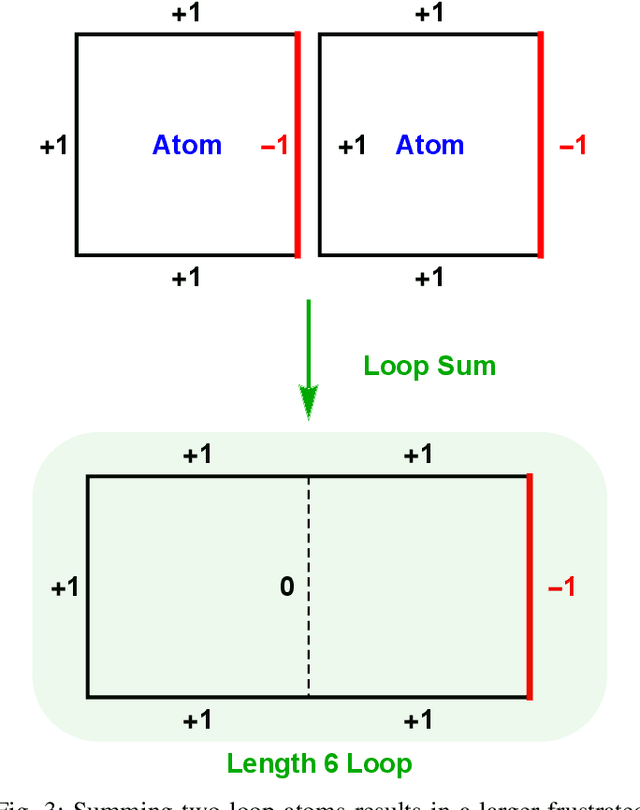

Abstract:Many optimization problems can be cast into the maximum satisfiability (MAX-SAT) form, and many solvers have been developed for tackling such problems. To evaluate the performance of a MAX-SAT solver, it is convenient to generate difficult MAX-SAT instances with solutions known in advance. Here, we propose a method of generating weighted MAX-2-SAT instances inspired by the frustrated-loop algorithm used by the quantum annealing community to generate Ising spin-glass instances with nearest-neighbor coupling. Our algorithm is extended to instances whose underlying coupling graph is general, though we focus here on the case of bipartite coupling, with the associated energy being the restricted Boltzmann machine (RBM) energy. It is shown that any MAX-2-SAT problem can be reduced to the problem of minimizing an RBM energy over the nodal values. The algorithm is designed such that the difficulty of the generated instances can be tuned through a central parameter known as the frustration index. Two versions of the algorithm are presented: the random- and structured-loop algorithms. For the random-loop algorithm, we provide a thorough theoretical and empirical analysis on its mathematical properties from the perspective of frustration, and observe empirically, using simulated annealing, a double phase transition behavior in the difficulty scaling behavior driven by the frustration index. For the structured-loop algorithm, we show that it offers an improvement in difficulty of the generated instances over the random-loop algorithm, with the improvement factor scaling super-exponentially with respect to the frustration index for instances at high loop density. At the end of the paper, we provide a brief discussion of the relevance of this work to the pre-training of RBMs.
Accelerating Deep Learning with Memcomputing
Oct 23, 2018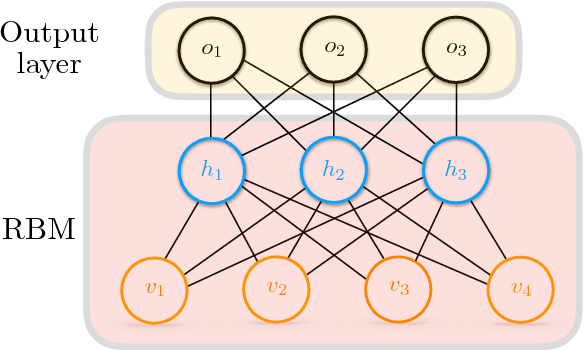
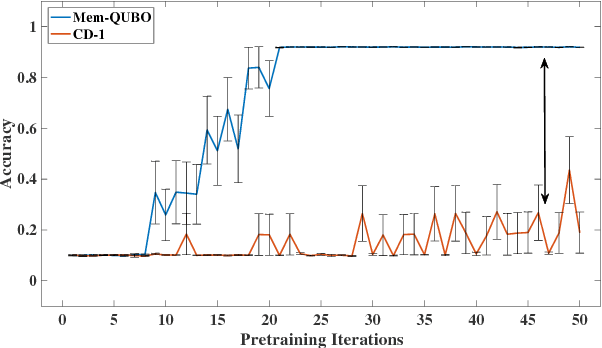
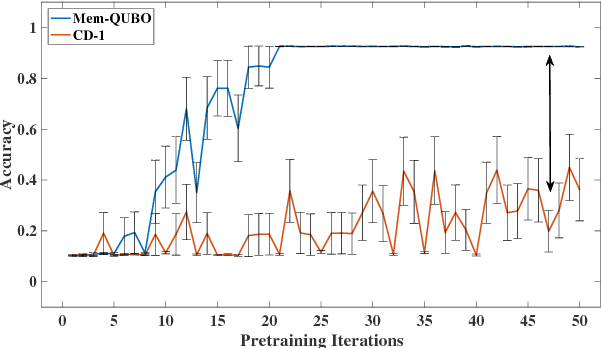
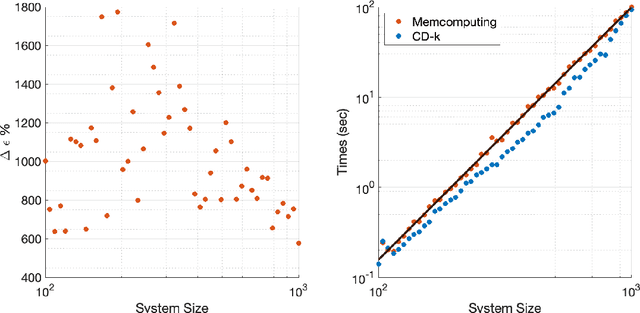
Abstract:Restricted Boltzmann machines (RBMs) and their extensions, called 'deep-belief networks', are powerful neural networks that have found applications in the fields of machine learning and artificial intelligence. The standard way to training these models resorts to an iterative unsupervised procedure based on Gibbs sampling, called 'contrastive divergence' (CD), and additional supervised tuning via back-propagation. However, this procedure has been shown not to follow any gradient and can lead to suboptimal solutions. In this paper, we show an efficient alternative to CD by means of simulations of digital memcomputing machines (DMMs). We test our approach on pattern recognition using a modified version of the MNIST data set. DMMs sample effectively the vast phase space given by the model distribution of the RBM, and provide a very good approximation close to the optimum. This efficient search significantly reduces the number of pretraining iterations necessary to achieve a given level of accuracy, as well as a total performance gain over CD. In fact, the acceleration of pretraining achieved by simulating DMMs is comparable to, in number of iterations, the recently reported hardware application of the quantum annealing method on the same network and data set. Notably, however, DMMs perform far better than the reported quantum annealing results in terms of quality of the training. We also compare our method to advances in supervised training, like batch-normalization and rectifiers, that work to reduce the advantage of pretraining. We find that the memcomputing method still maintains a quality advantage ($>1\%$ in accuracy, and a $20\%$ reduction in error rate) over these approaches. Furthermore, our method is agnostic about the connectivity of the network. Therefore, it can be extended to train full Boltzmann machines, and even deep networks at once.
Memcomputing: Leveraging memory and physics to compute efficiently
May 06, 2018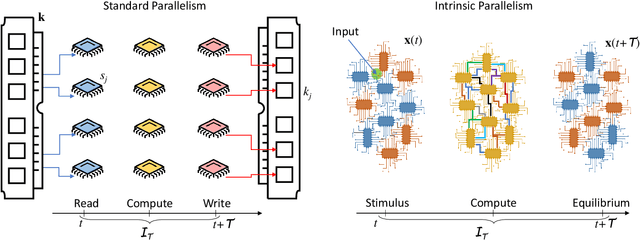
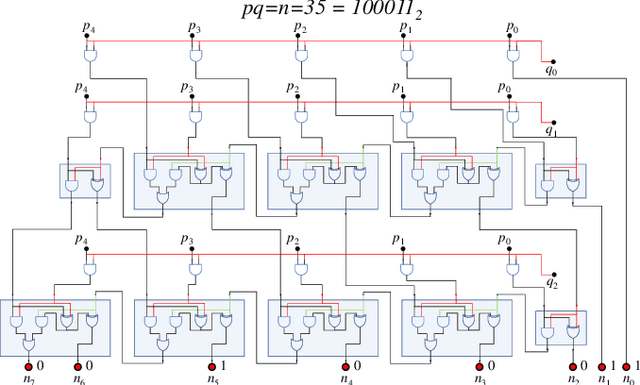
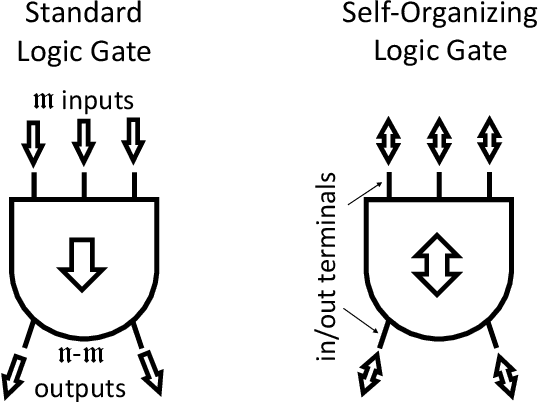
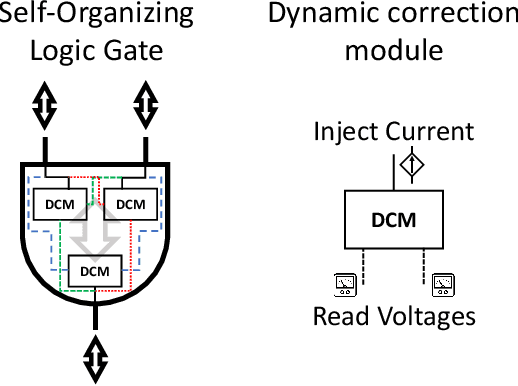
Abstract:It is well known that physical phenomena may be of great help in computing some difficult problems efficiently. A typical example is prime factorization that may be solved in polynomial time by exploiting quantum entanglement on a quantum computer. There are, however, other types of (non-quantum) physical properties that one may leverage to compute efficiently a wide range of hard problems. In this perspective we discuss how to employ one such property, memory (time non-locality), in a novel physics-based approach to computation: Memcomputing. In particular, we focus on digital memcomputing machines (DMMs) that are scalable. DMMs can be realized with non-linear dynamical systems with memory. The latter property allows the realization of a new type of Boolean logic, one that is self-organizing. Self-organizing logic gates are "terminal-agnostic", namely they do not distinguish between input and output terminals. When appropriately assembled to represent a given combinatorial/optimization problem, the corresponding self-organizing circuit converges to the equilibrium points that express the solutions of the problem at hand. In doing so, DMMs take advantage of the long-range order that develops during the transient dynamics. This collective dynamical behavior, reminiscent of a phase transition, or even the "edge of chaos", is mediated by families of classical trajectories (instantons) that connect critical points of increasing stability in the system's phase space. The topological character of the solution search renders DMMs robust against noise and structural disorder. Since DMMs are non-quantum systems described by ordinary differential equations, not only can they be built in hardware with available technology, they can also be simulated efficiently on modern classical computers. As an example, we will show the polynomial-time solution of the subset-sum problem for the worst...
On the Universality of Memcomputing Machines
Dec 23, 2017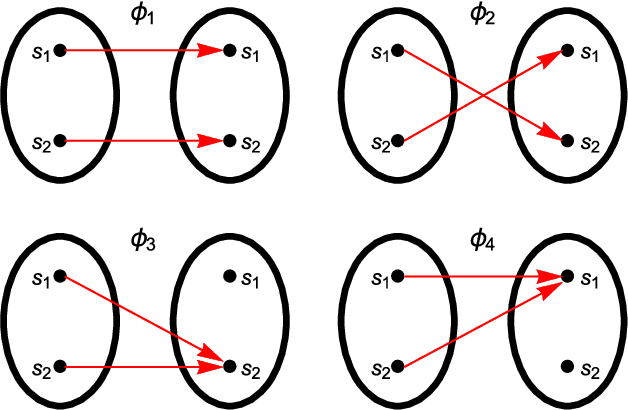
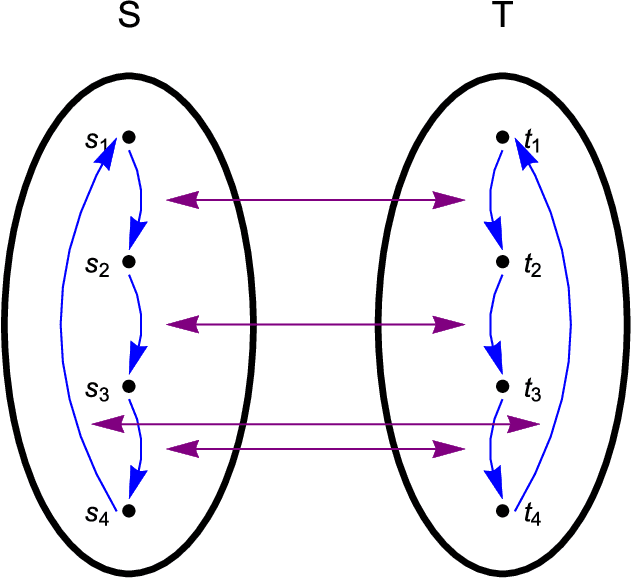
Abstract:Universal memcomputing machines (UMMs) [IEEE Trans. Neural Netw. Learn. Syst. 26, 2702 (2015)] represent a novel computational model in which memory (time non-locality) accomplishes both tasks of storing and processing of information. UMMs have been shown to be Turing-complete, namely they can simulate any Turing machine. In this paper, using set theory and cardinality arguments, we compare them with liquid-state machines (or "reservoir computing") and quantum machines ("quantum computing"). We show that UMMs can simulate both types of machines, hence they are both "liquid-" or "reservoir-complete" and "quantum-complete". Of course, these statements pertain only to the type of problems these machines can solve, and not to the amount of resources required for such simulations. Nonetheless, the method presented here provides a general framework in which to describe the relation between UMMs and any other type of computational model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge