Directed percolation and numerical stability of simulations of digital memcomputing machines
Paper and Code
Feb 06, 2021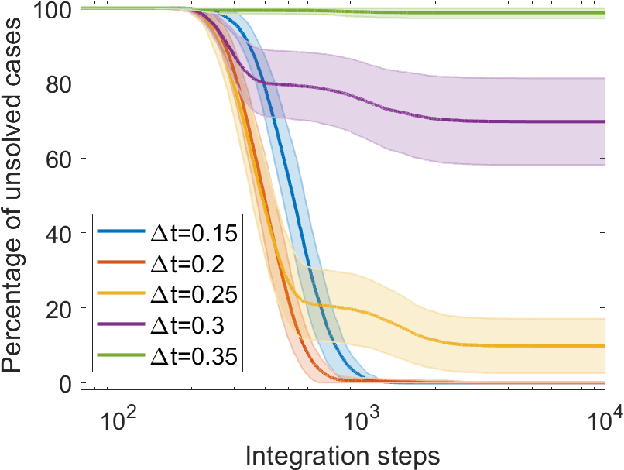
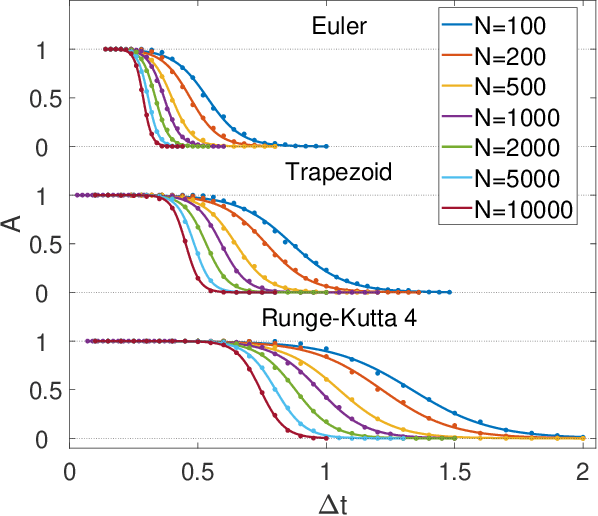
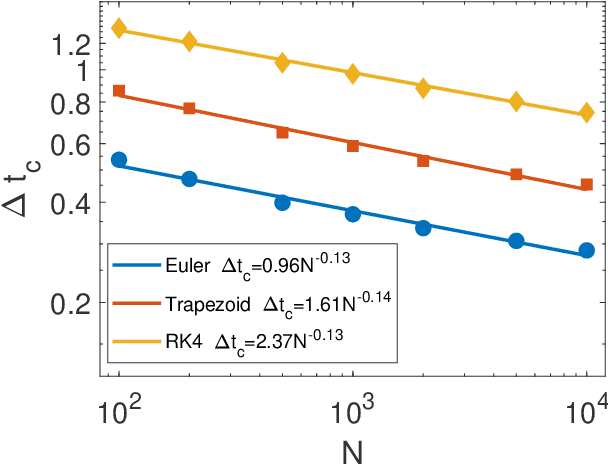
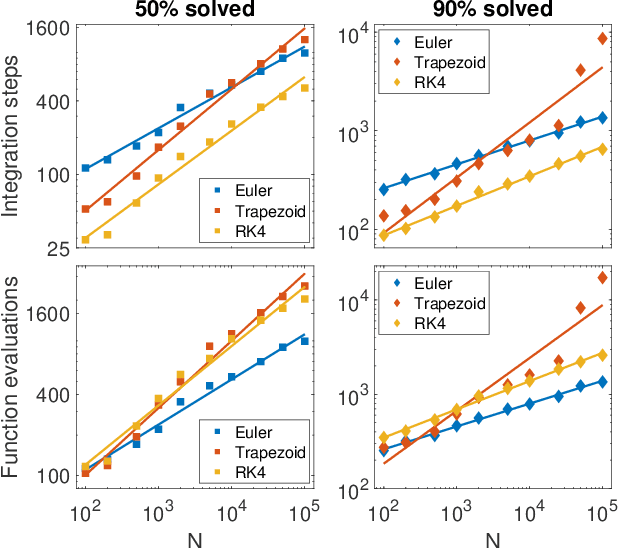
Digital memcomputing machines (DMMs) are a novel, non-Turing class of machines designed to solve combinatorial optimization problems. They can be physically realized with continuous-time, non-quantum dynamical systems with memory (time non-locality), whose ordinary differential equations (ODEs) can be numerically integrated on modern computers. Solutions of many hard problems have been reported by numerically integrating the ODEs of DMMs, showing substantial advantages over state-of-the-art solvers. To investigate the reasons behind the robustness and effectiveness of this method, we employ three explicit integration schemes (forward Euler, trapezoid and Runge-Kutta 4th order) with a constant time step, to solve 3-SAT instances with planted solutions. We show that, (i) even if most of the trajectories in the phase space are destroyed by numerical noise, the solution can still be achieved; (ii) the forward Euler method, although having the largest numerical error, solves the instances in the least amount of function evaluations; and (iii) when increasing the integration time step, the system undergoes a "solvable-unsolvable transition" at a critical threshold, which needs to decay at most as a power law with the problem size, to control the numerical errors. To explain these results, we model the dynamical behavior of DMMs as directed percolation of the state trajectory in the phase space in the presence of noise. This viewpoint clarifies the reasons behind their numerical robustness and provides an analytical understanding of the unsolvable-solvable transition. These results land further support to the usefulness of DMMs in the solution of hard combinatorial optimization problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge