Yuan-Hang Zhang
Artificial intelligence for representing and characterizing quantum systems
Sep 05, 2025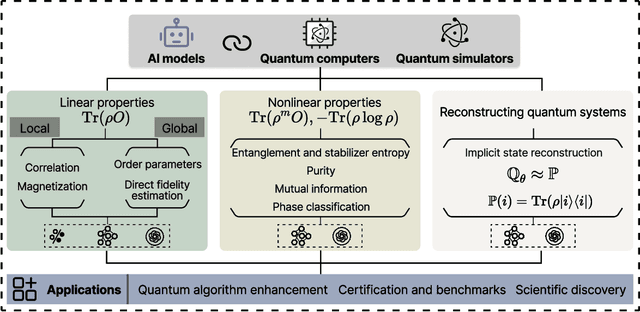
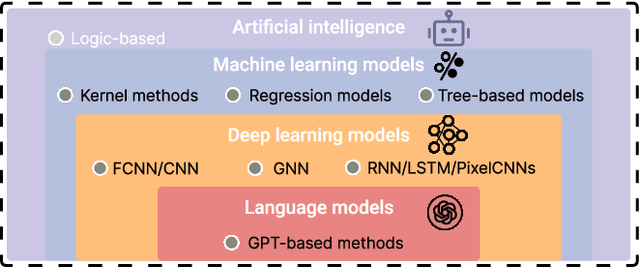
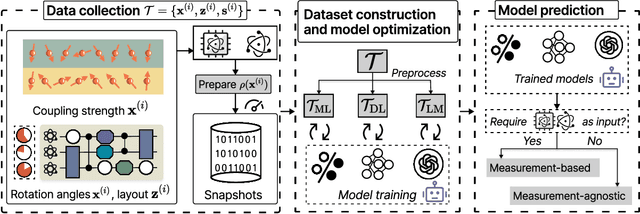
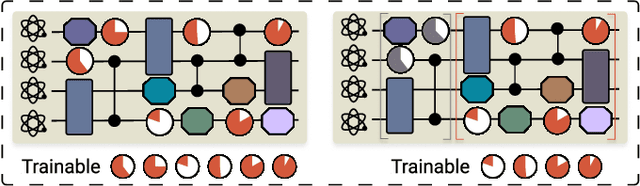
Abstract:Efficient characterization of large-scale quantum systems, especially those produced by quantum analog simulators and megaquop quantum computers, poses a central challenge in quantum science due to the exponential scaling of the Hilbert space with respect to system size. Recent advances in artificial intelligence (AI), with its aptitude for high-dimensional pattern recognition and function approximation, have emerged as a powerful tool to address this challenge. A growing body of research has leveraged AI to represent and characterize scalable quantum systems, spanning from theoretical foundations to experimental realizations. Depending on how prior knowledge and learning architectures are incorporated, the integration of AI into quantum system characterization can be categorized into three synergistic paradigms: machine learning, and, in particular, deep learning and language models. This review discusses how each of these AI paradigms contributes to two core tasks in quantum systems characterization: quantum property prediction and the construction of surrogates for quantum states. These tasks underlie diverse applications, from quantum certification and benchmarking to the enhancement of quantum algorithms and the understanding of strongly correlated phases of matter. Key challenges and open questions are also discussed, together with future prospects at the interface of AI and quantum science.
A Generative Neural Annealer for Black-Box Combinatorial Optimization
May 14, 2025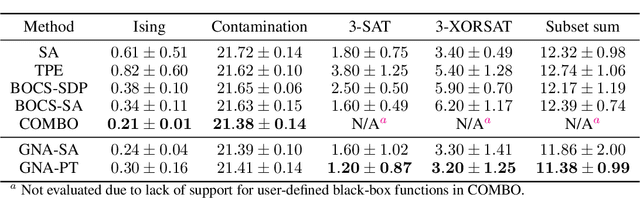
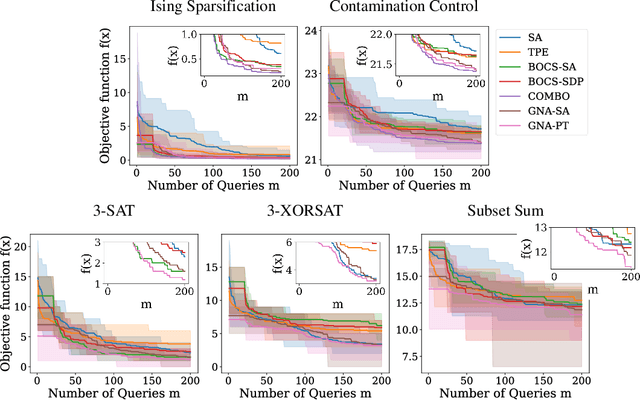
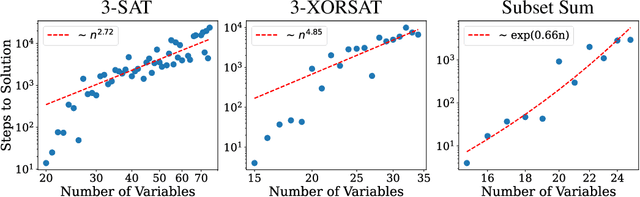
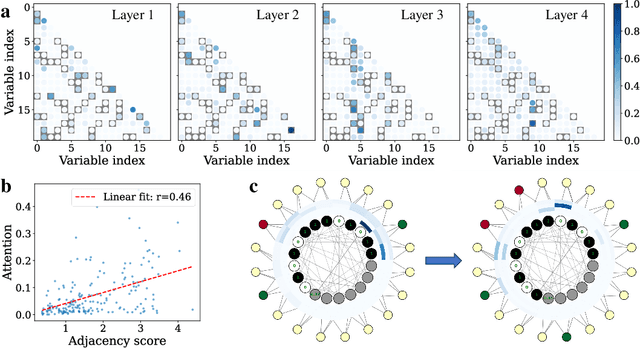
Abstract:We propose a generative, end-to-end solver for black-box combinatorial optimization that emphasizes both sample efficiency and solution quality on NP problems. Drawing inspiration from annealing-based algorithms, we treat the black-box objective as an energy function and train a neural network to model the associated Boltzmann distribution. By conditioning on temperature, the network captures a continuum of distributions--from near-uniform at high temperatures to sharply peaked around global optima at low temperatures--thereby learning the structure of the energy landscape and facilitating global optimization. When queries are expensive, the temperature-dependent distributions naturally enable data augmentation and improve sample efficiency. When queries are cheap but the problem remains hard, the model learns implicit variable interactions, effectively "opening" the black box. We validate our approach on challenging combinatorial tasks under both limited and unlimited query budgets, showing competitive performance against state-of-the-art black-box optimizers.
Implementation of digital MemComputing using standard electronic components
Oct 03, 2023



Abstract:Digital MemComputing machines (DMMs), which employ nonlinear dynamical systems with memory (time non-locality), have proven to be a robust and scalable unconventional computing approach for solving a wide variety of combinatorial optimization problems. However, most of the research so far has focused on the numerical simulations of the equations of motion of DMMs. This inevitably subjects time to discretization, which brings its own (numerical) issues that would be absent in actual physical systems operating in continuous time. Although hardware realizations of DMMs have been previously suggested, their implementation would require materials and devices that are not so easy to integrate with traditional electronics. In this study, we propose a novel hardware design for DMMs that leverages only conventional electronic components. Our findings suggest that this design offers a marked improvement in speed compared to existing realizations of these machines, without requiring special materials or novel device concepts. We also show that these DMMs are robust against additive noise. Moreover, the absence of numerical noise promises enhanced stability over extended periods of the machines' operation, paving the way for addressing even more complex problems.
Self-Averaging of Digital MemComputing Machines
Jan 20, 2023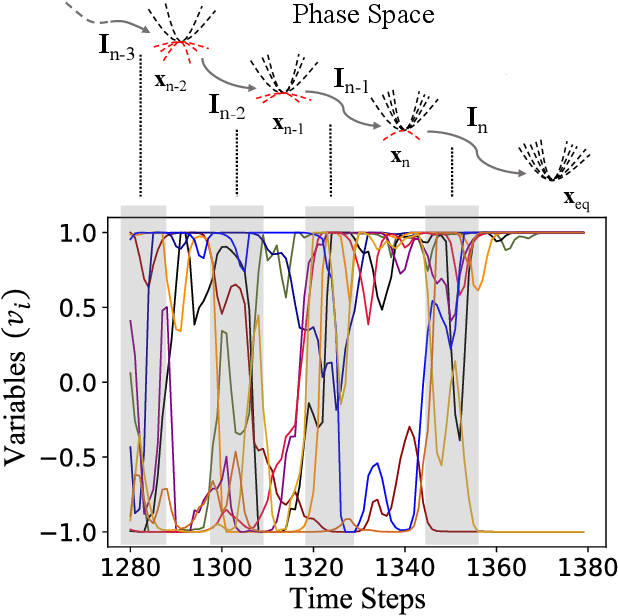
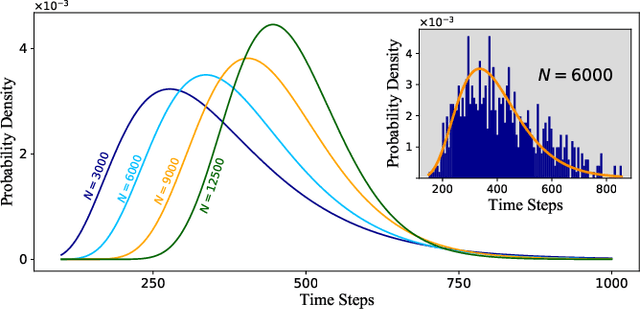
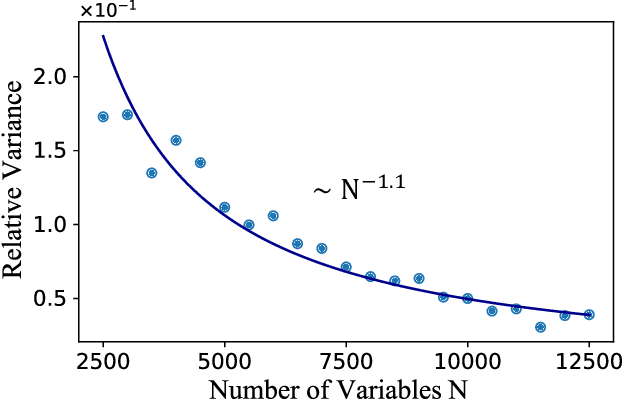
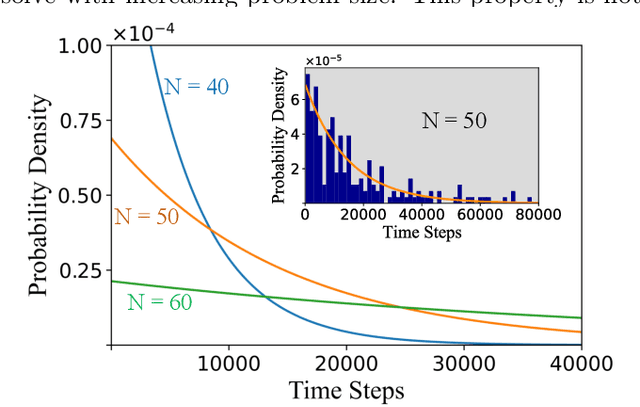
Abstract:Digital MemComputing machines (DMMs) are a new class of computing machines that employ non-quantum dynamical systems with memory to solve combinatorial optimization problems. Here, we show that the time to solution (TTS) of DMMs follows an inverse Gaussian distribution, with the TTS self-averaging with increasing problem size, irrespective of the problem they solve. We provide both an analytical understanding of this phenomenon and numerical evidence by solving instances of the 3-SAT (satisfiability) problem. The self-averaging property of DMMs with problem size implies that they are increasingly insensitive to the detailed features of the instances they solve. This is in sharp contrast to traditional algorithms applied to the same problems, illustrating another advantage of this physics-based approach to computation.
Directed percolation and numerical stability of simulations of digital memcomputing machines
Feb 06, 2021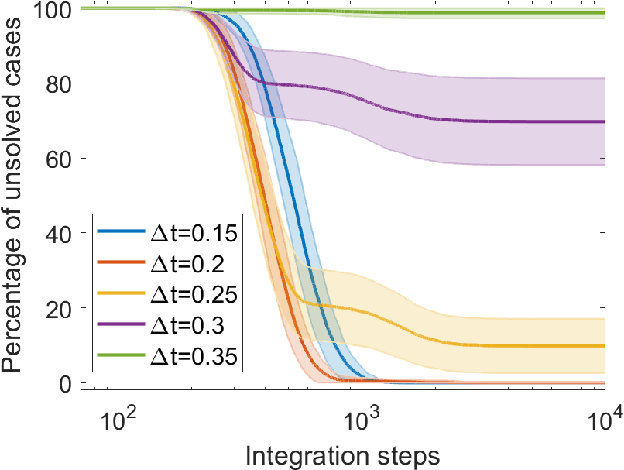
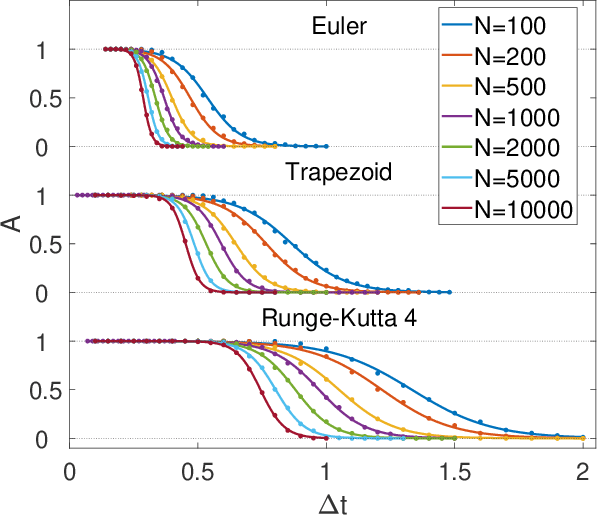
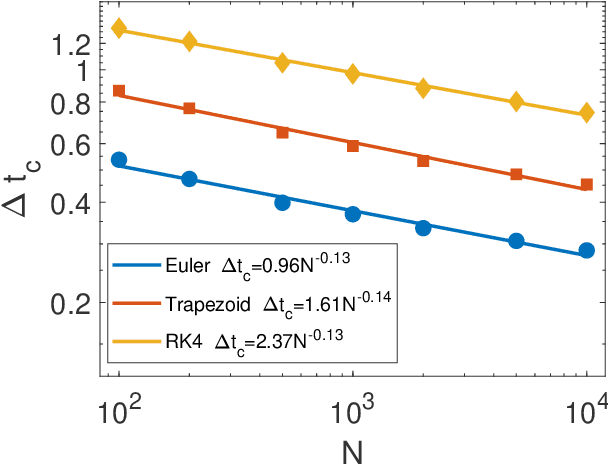
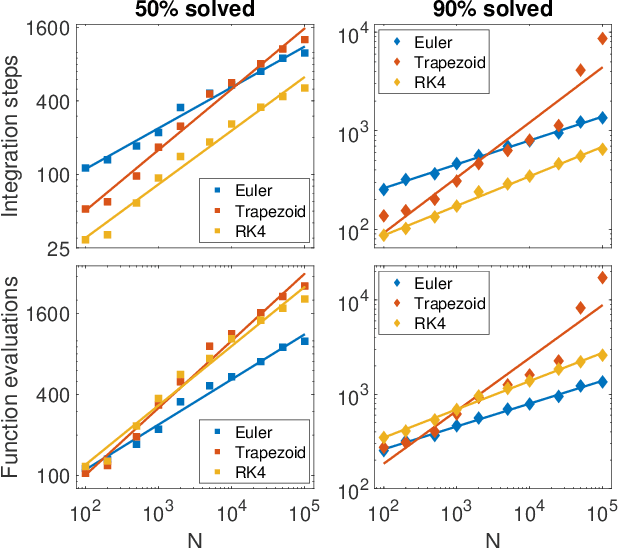
Abstract:Digital memcomputing machines (DMMs) are a novel, non-Turing class of machines designed to solve combinatorial optimization problems. They can be physically realized with continuous-time, non-quantum dynamical systems with memory (time non-locality), whose ordinary differential equations (ODEs) can be numerically integrated on modern computers. Solutions of many hard problems have been reported by numerically integrating the ODEs of DMMs, showing substantial advantages over state-of-the-art solvers. To investigate the reasons behind the robustness and effectiveness of this method, we employ three explicit integration schemes (forward Euler, trapezoid and Runge-Kutta 4th order) with a constant time step, to solve 3-SAT instances with planted solutions. We show that, (i) even if most of the trajectories in the phase space are destroyed by numerical noise, the solution can still be achieved; (ii) the forward Euler method, although having the largest numerical error, solves the instances in the least amount of function evaluations; and (iii) when increasing the integration time step, the system undergoes a "solvable-unsolvable transition" at a critical threshold, which needs to decay at most as a power law with the problem size, to control the numerical errors. To explain these results, we model the dynamical behavior of DMMs as directed percolation of the state trajectory in the phase space in the presence of noise. This viewpoint clarifies the reasons behind their numerical robustness and provides an analytical understanding of the unsolvable-solvable transition. These results land further support to the usefulness of DMMs in the solution of hard combinatorial optimization problems.
Topological Quantum Compiling with Reinforcement Learning
Apr 09, 2020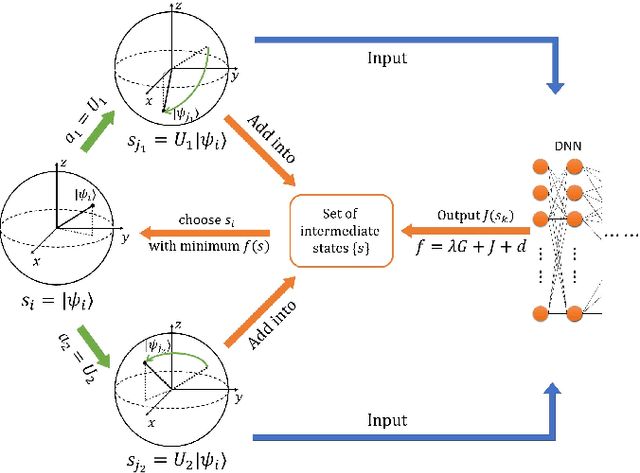
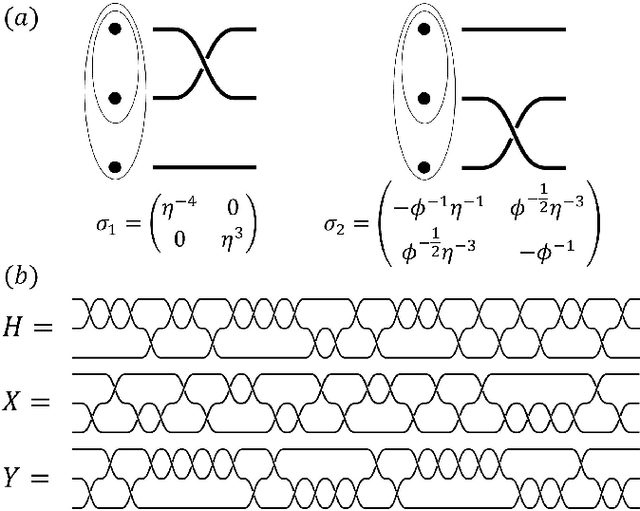
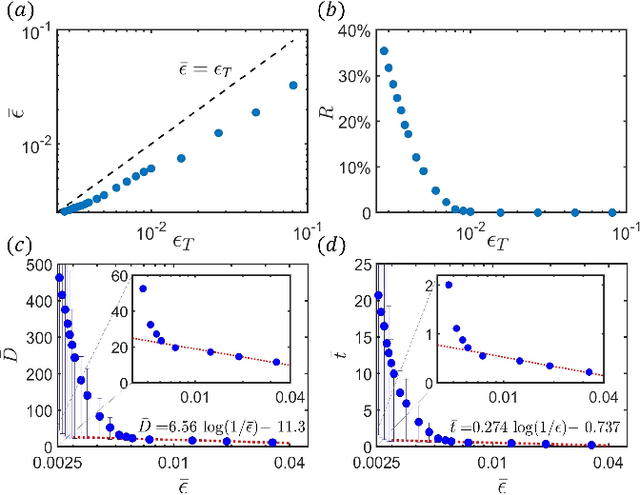
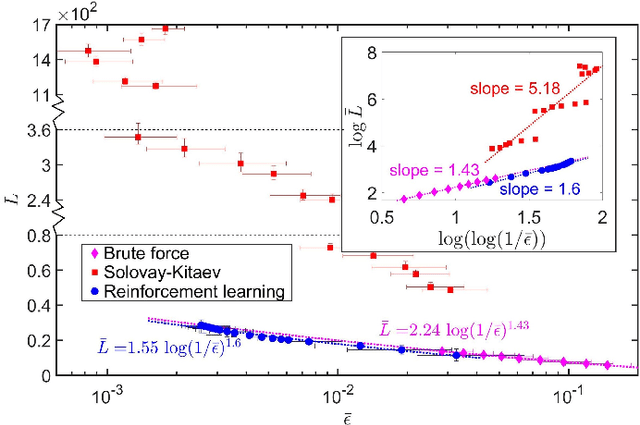
Abstract:Quantum compiling, a process that decomposes the quantum algorithm into a series of hardware-compatible commands or elementary gates, is of fundamental importance for quantum computing. In this paper, we introduce an efficient algorithm based on deep reinforcement learning that compiles an arbitrary single-qubit gate into a sequence of elementary gates from a finite universal set. This algorithm is inspired by an interesting observation that the task of decomposing unitaries into a sequence of hardware-compatible elementary gates is analogous to the task of working out a sequence of basic moves that solves the Rubik's cube. It generates near-optimal gate sequences with given accuracy and is generally applicable to various scenarios, independent of the hardware-feasible universal set and free from using ancillary qubits. For concreteness, we apply this algorithm to the case of topological compiling of Fibonacci anyons and show that it indeed finds the near-optimal braiding sequences for approximating an arbitrary single-qubit unitary. Our algorithm may carry over to other challenging quantum discrete problems, thus opens up a new avenue for intriguing applications of deep learning in quantum physics.
$M^3$T: Multi-Modal Continuous Valence-Arousal Estimation in the Wild
Feb 07, 2020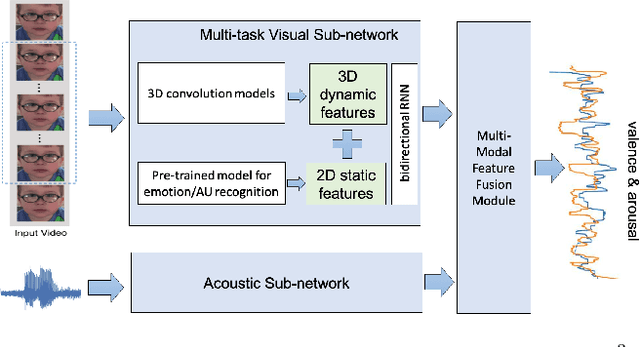
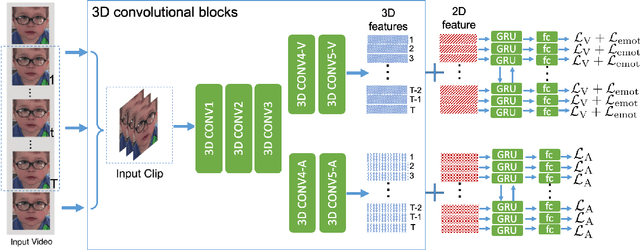
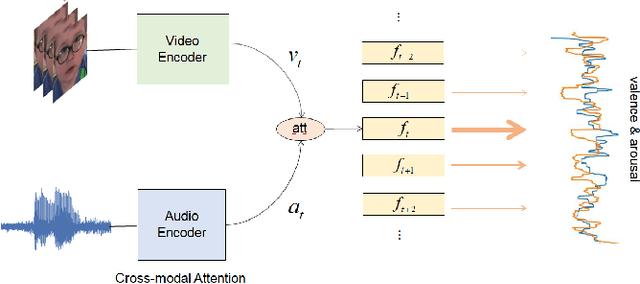
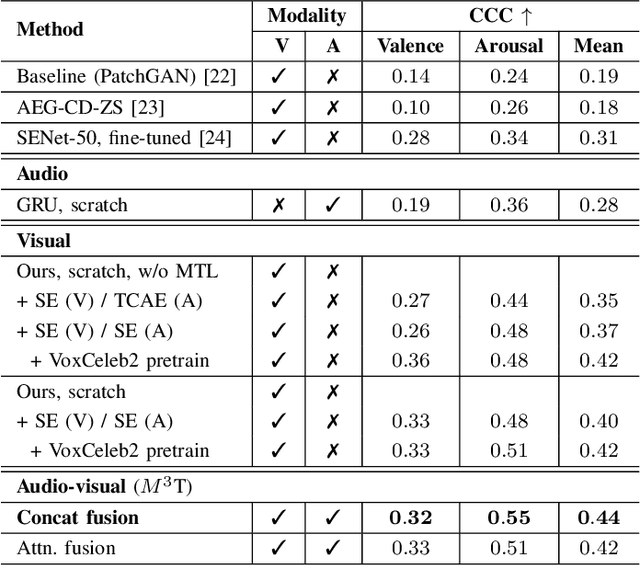
Abstract:This report describes a multi-modal multi-task ($M^3$T) approach underlying our submission to the valence-arousal estimation track of the Affective Behavior Analysis in-the-wild (ABAW) Challenge, held in conjunction with the IEEE International Conference on Automatic Face and Gesture Recognition (FG) 2020. In the proposed $M^3$T framework, we fuse both visual features from videos and acoustic features from the audio tracks to estimate the valence and arousal. The spatio-temporal visual features are extracted with a 3D convolutional network and a bidirectional recurrent neural network. Considering the correlations between valence / arousal, emotions, and facial actions, we also explores mechanisms to benefit from other tasks. We evaluated the $M^3$T framework on the validation set provided by ABAW and it significantly outperforms the baseline method.
A Digital Fuzzy Edge Detector for Color Images
Jan 13, 2017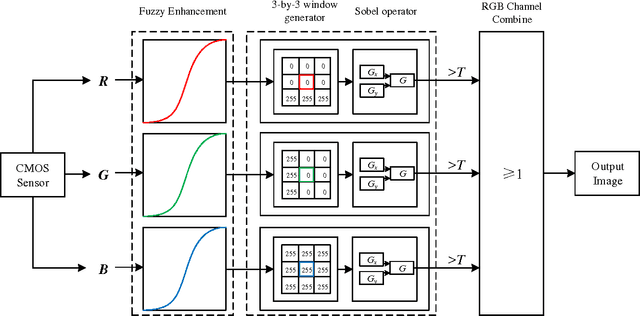

Abstract:Edge detection is a classic problem in the field of image processing, which lays foundations for other tasks such as image segmentation. Conventionally, this operation is performed using gradient operators such as the Roberts or Sobel operator, which can discover local changes in intensity levels. These operators, however, perform poorly on low contrast images. In this paper, we propose an edge detector architecture for color images based on fuzzy theory and the Sobel operator. First, the R, G and B channels are extracted from an image and enhanced using fuzzy methods, in order to suppress noise and improve the contrast between the background and the objects. The Sobel operator is then applied to each of the channels, which are finally combined into an edge map of the origin image. Experimental results obtained through an FPGA-based implementation have proved the proposed method effective.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge