Topological Quantum Compiling with Reinforcement Learning

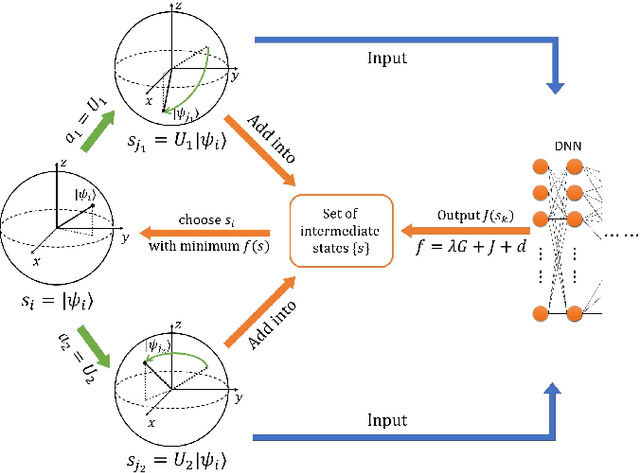
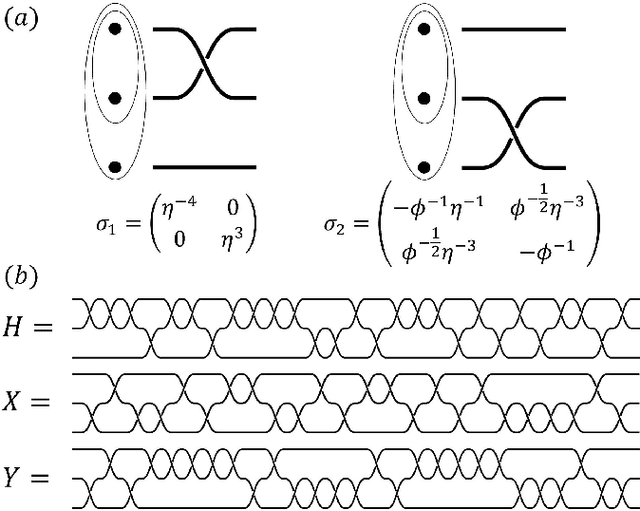
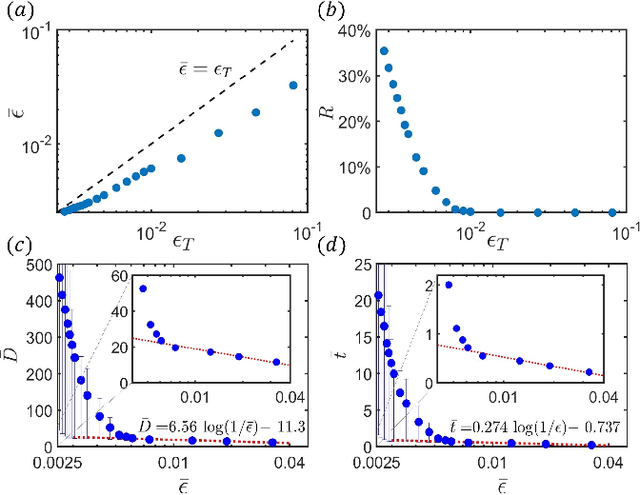
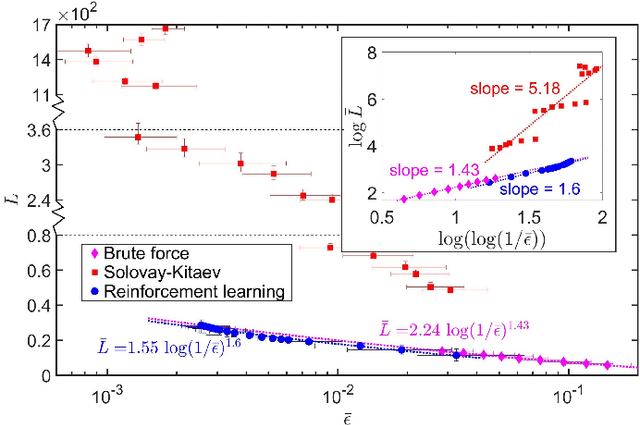
Quantum compiling, a process that decomposes the quantum algorithm into a series of hardware-compatible commands or elementary gates, is of fundamental importance for quantum computing. In this paper, we introduce an efficient algorithm based on deep reinforcement learning that compiles an arbitrary single-qubit gate into a sequence of elementary gates from a finite universal set. This algorithm is inspired by an interesting observation that the task of decomposing unitaries into a sequence of hardware-compatible elementary gates is analogous to the task of working out a sequence of basic moves that solves the Rubik's cube. It generates near-optimal gate sequences with given accuracy and is generally applicable to various scenarios, independent of the hardware-feasible universal set and free from using ancillary qubits. For concreteness, we apply this algorithm to the case of topological compiling of Fibonacci anyons and show that it indeed finds the near-optimal braiding sequences for approximating an arbitrary single-qubit unitary. Our algorithm may carry over to other challenging quantum discrete problems, thus opens up a new avenue for intriguing applications of deep learning in quantum physics.