A quantum neural network with efficient optimization and interpretability

As the quantum counterparts to the classical artificial neural networks underlying widespread machine-learning applications, unitary-based quantum neural networks are active in various fields of quantum computation. Despite the potential, their developments have been hampered by the elevated cost of optimizations and difficulty in realizations. Here, we propose a quantum neural network in the form of fermion models whose physical properties, such as the local density of states and conditional conductance, serve as outputs, and establish an efficient optimization comparable to back-propagation. In addition to competitive accuracy on challenging classical machine-learning benchmarks, our fermion quantum neural network performs machine learning on quantum systems with high precision and without preprocessing. The quantum nature also brings various other advantages, e.g., quantum correlations entitle networks with more general and local connectivity facilitating numerical simulations and experimental realizations, as well as novel perspectives to address the vanishing gradient problem long plaguing deep networks. We also demonstrate the applications of our quantum toolbox, such as quantum-entanglement analysis, for interpretable machine learning, including training dynamics, decision logic flow, and criteria formulation.

Topological Quantum Compiling with Reinforcement Learning

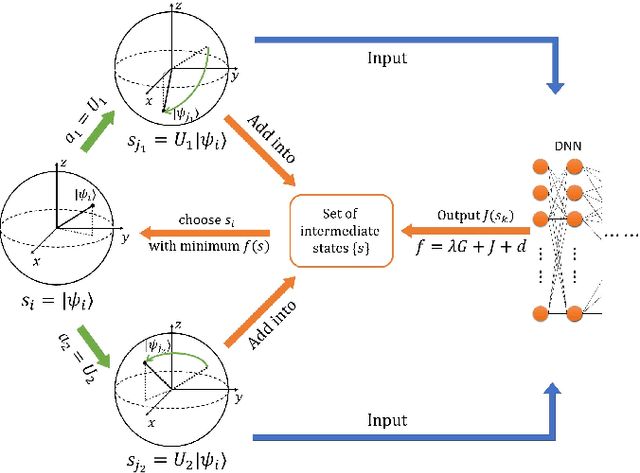
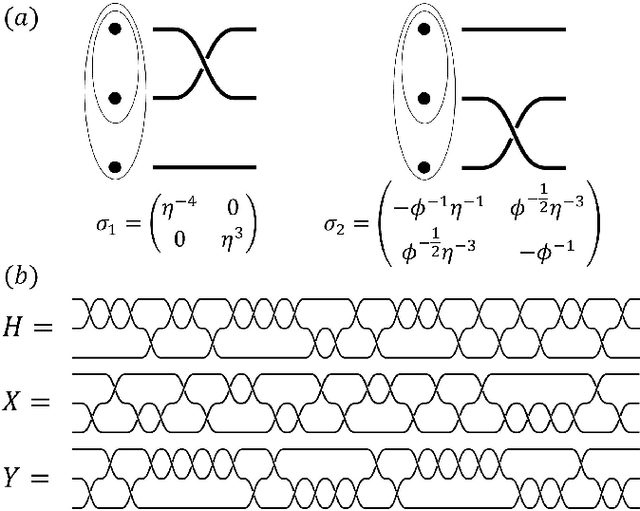
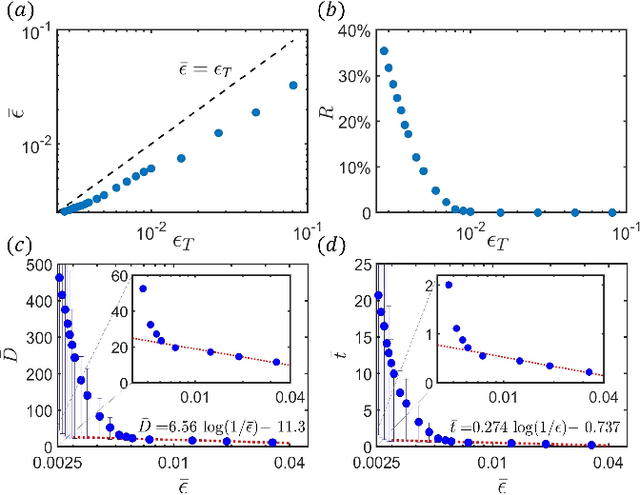
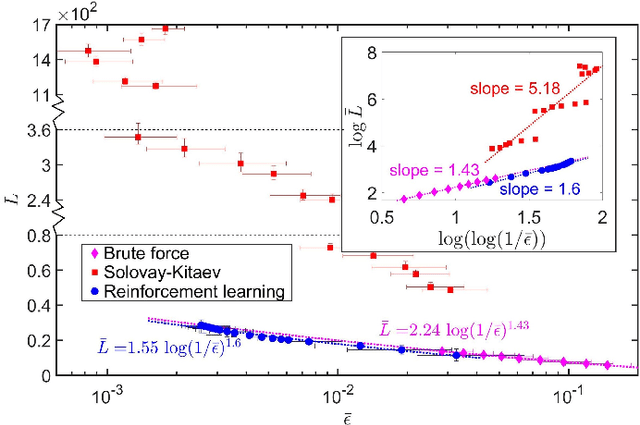
Quantum compiling, a process that decomposes the quantum algorithm into a series of hardware-compatible commands or elementary gates, is of fundamental importance for quantum computing. In this paper, we introduce an efficient algorithm based on deep reinforcement learning that compiles an arbitrary single-qubit gate into a sequence of elementary gates from a finite universal set. This algorithm is inspired by an interesting observation that the task of decomposing unitaries into a sequence of hardware-compatible elementary gates is analogous to the task of working out a sequence of basic moves that solves the Rubik's cube. It generates near-optimal gate sequences with given accuracy and is generally applicable to various scenarios, independent of the hardware-feasible universal set and free from using ancillary qubits. For concreteness, we apply this algorithm to the case of topological compiling of Fibonacci anyons and show that it indeed finds the near-optimal braiding sequences for approximating an arbitrary single-qubit unitary. Our algorithm may carry over to other challenging quantum discrete problems, thus opens up a new avenue for intriguing applications of deep learning in quantum physics.