Daniel Primosch
Self-Averaging of Digital MemComputing Machines
Jan 20, 2023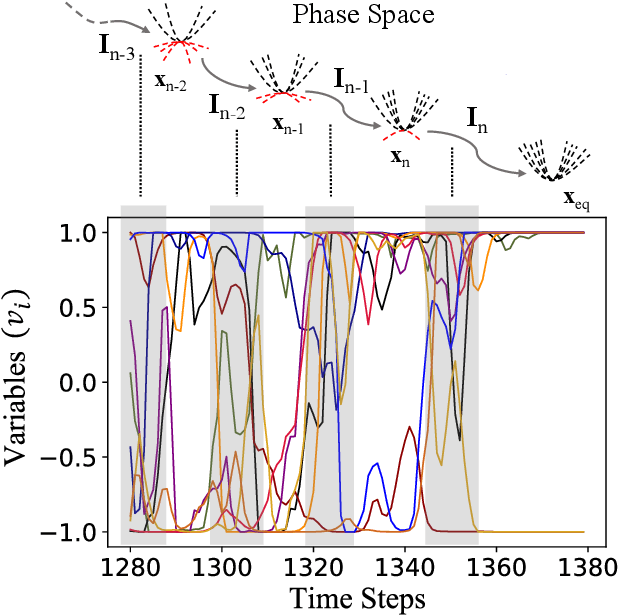
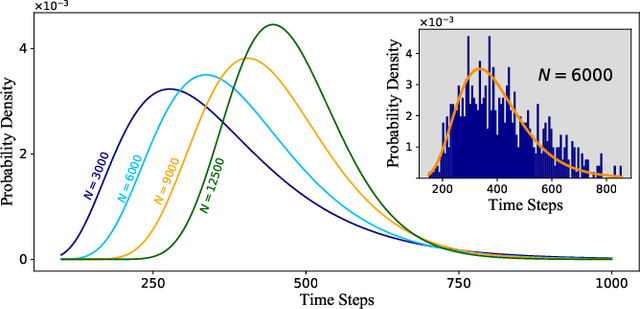
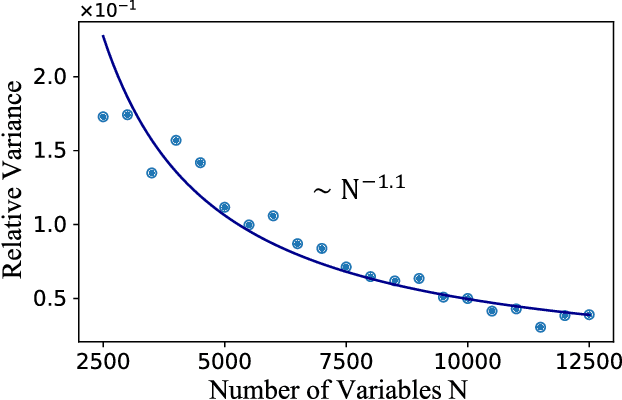
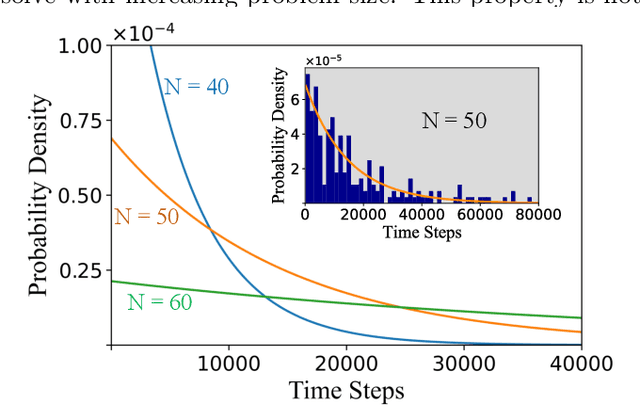
Abstract:Digital MemComputing machines (DMMs) are a new class of computing machines that employ non-quantum dynamical systems with memory to solve combinatorial optimization problems. Here, we show that the time to solution (TTS) of DMMs follows an inverse Gaussian distribution, with the TTS self-averaging with increasing problem size, irrespective of the problem they solve. We provide both an analytical understanding of this phenomenon and numerical evidence by solving instances of the 3-SAT (satisfiability) problem. The self-averaging property of DMMs with problem size implies that they are increasingly insensitive to the detailed features of the instances they solve. This is in sharp contrast to traditional algorithms applied to the same problems, illustrating another advantage of this physics-based approach to computation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge