Accelerating Deep Learning with Memcomputing
Paper and Code
Oct 23, 2018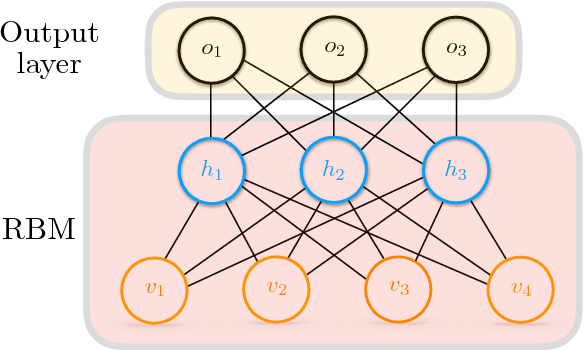
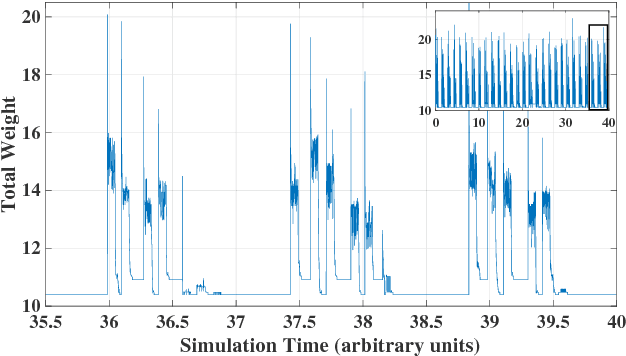
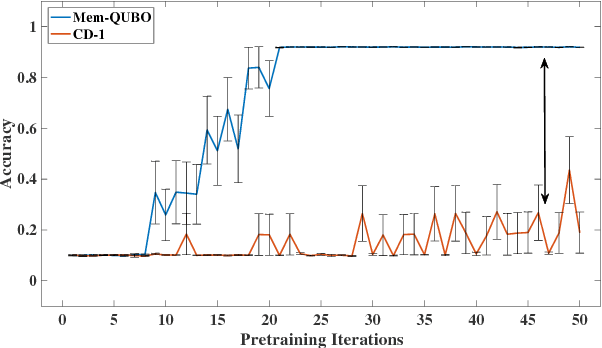
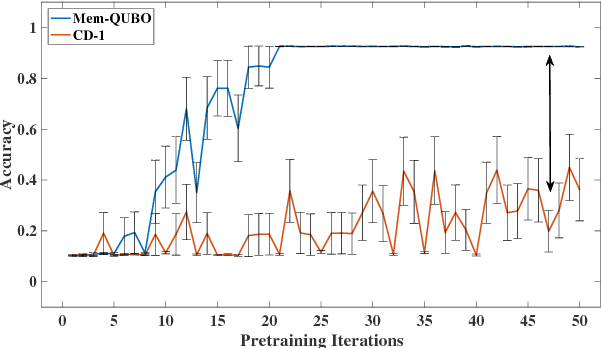
Restricted Boltzmann machines (RBMs) and their extensions, called 'deep-belief networks', are powerful neural networks that have found applications in the fields of machine learning and artificial intelligence. The standard way to training these models resorts to an iterative unsupervised procedure based on Gibbs sampling, called 'contrastive divergence' (CD), and additional supervised tuning via back-propagation. However, this procedure has been shown not to follow any gradient and can lead to suboptimal solutions. In this paper, we show an efficient alternative to CD by means of simulations of digital memcomputing machines (DMMs). We test our approach on pattern recognition using a modified version of the MNIST data set. DMMs sample effectively the vast phase space given by the model distribution of the RBM, and provide a very good approximation close to the optimum. This efficient search significantly reduces the number of pretraining iterations necessary to achieve a given level of accuracy, as well as a total performance gain over CD. In fact, the acceleration of pretraining achieved by simulating DMMs is comparable to, in number of iterations, the recently reported hardware application of the quantum annealing method on the same network and data set. Notably, however, DMMs perform far better than the reported quantum annealing results in terms of quality of the training. We also compare our method to advances in supervised training, like batch-normalization and rectifiers, that work to reduce the advantage of pretraining. We find that the memcomputing method still maintains a quality advantage ($>1\%$ in accuracy, and a $20\%$ reduction in error rate) over these approaches. Furthermore, our method is agnostic about the connectivity of the network. Therefore, it can be extended to train full Boltzmann machines, and even deep networks at once.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge