Mode-Assisted Joint Training of Deep Boltzmann Machines

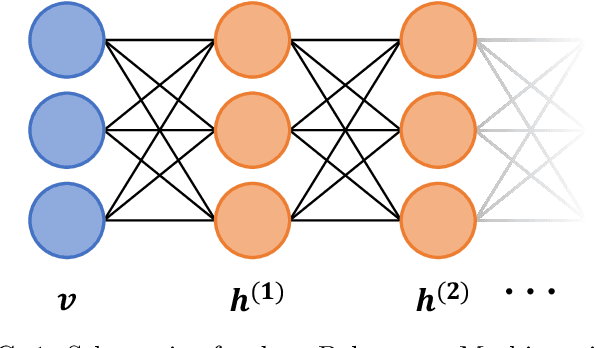
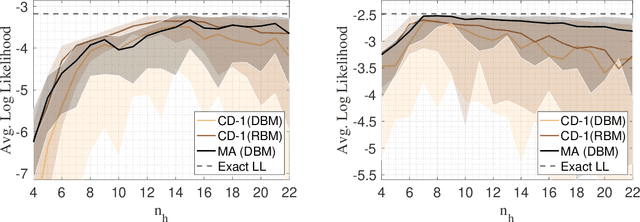
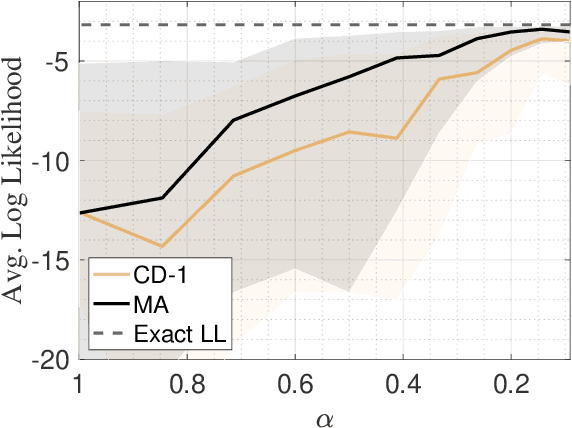
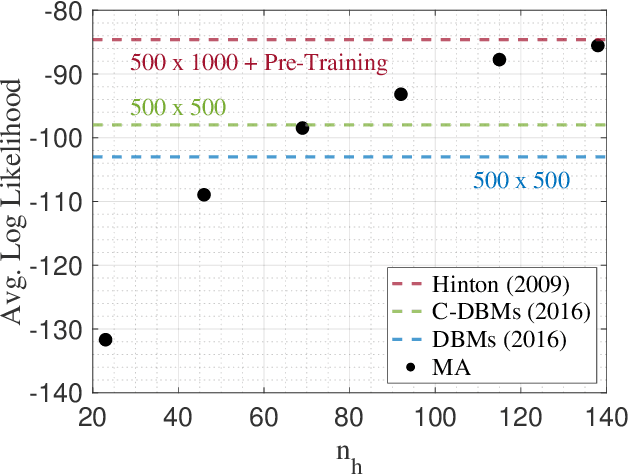
The deep extension of the restricted Boltzmann machine (RBM), known as the deep Boltzmann machine (DBM), is an expressive family of machine learning models which can serve as compact representations of complex probability distributions. However, jointly training DBMs in the unsupervised setting has proven to be a formidable task. A recent technique we have proposed, called mode-assisted training, has shown great success in improving the unsupervised training of RBMs. Here, we show that the performance gains of the mode-assisted training are even more dramatic for DBMs. In fact, DBMs jointly trained with the mode-assisted algorithm can represent the same data set with orders of magnitude lower number of total parameters compared to state-of-the-art training procedures and even with respect to RBMs, provided a fan-in network topology is also introduced. This substantial saving in number of parameters makes this training method very appealing also for hardware implementations.

Mode-Assisted Unsupervised Learning of Restricted Boltzmann Machines

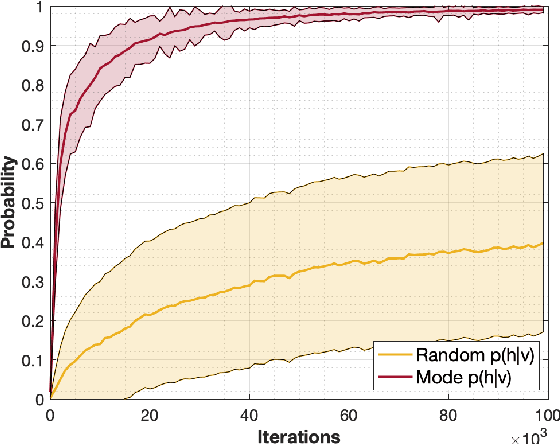
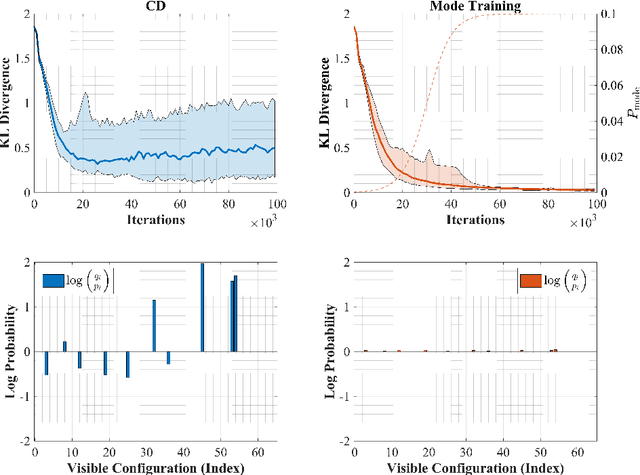
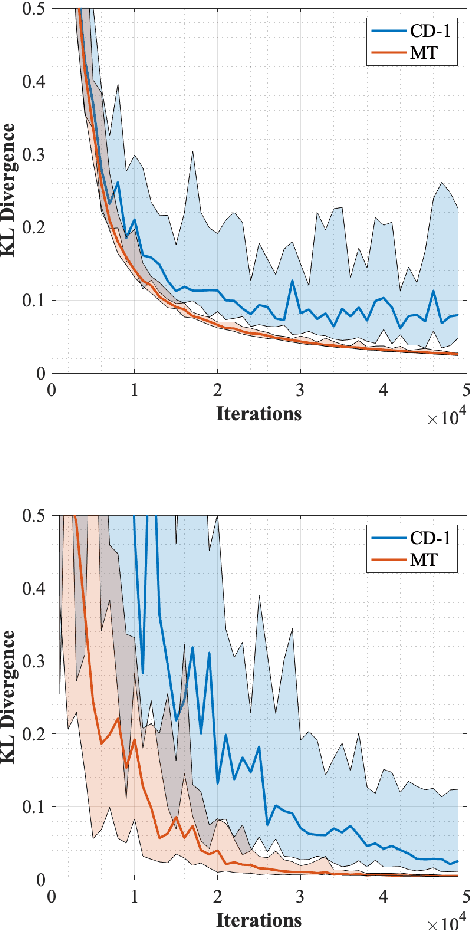
Restricted Boltzmann machines (RBMs) are a powerful class of generative models, but their training requires computing a gradient that, unlike supervised backpropagation on typical loss functions, is notoriously difficult even to approximate. Here, we show that properly combining standard gradient updates with an off-gradient direction, constructed from samples of the RBM ground state (mode), improves their training dramatically over traditional gradient methods. This approach, which we call mode training, promotes faster training and stability, in addition to lower converged relative entropy (KL divergence). Along with the proofs of stability and convergence of this method, we also demonstrate its efficacy on synthetic datasets where we can compute KL divergences exactly, as well as on a larger machine learning standard, MNIST. The mode training we suggest is quite versatile, as it can be applied in conjunction with any given gradient method, and is easily extended to more general energy-based neural network structures such as deep, convolutional and unrestricted Boltzmann machines.

Data Generation for Neural Programming by Example

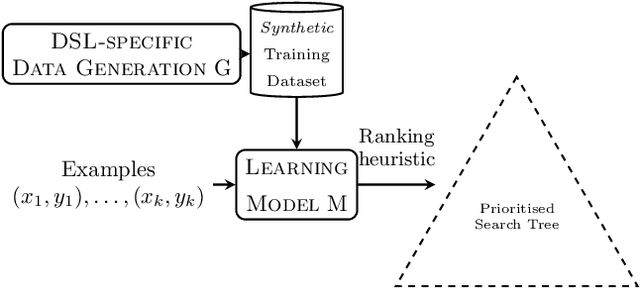
Programming by example is the problem of synthesizing a program from a small set of input / output pairs. Recent works applying machine learning methods to this task show promise, but are typically reliant on generating synthetic examples for training. A particular challenge lies in generating meaningful sets of inputs and outputs, which well-characterize a given program and accurately demonstrate its behavior. Where examples used for testing are generated by the same method as training data then the performance of a model may be partly reliant on this similarity. In this paper we introduce a novel approach using an SMT solver to synthesize inputs which cover a diverse set of behaviors for a given program. We carry out a case study comparing this method to existing synthetic data generation procedures in the literature, and find that data generated using our approach improves both the discriminatory power of example sets and the ability of trained machine learning models to generalize to unfamiliar data.

Generating Weighted MAX-2-SAT Instances of Tunable Difficulty with Frustrated Loops

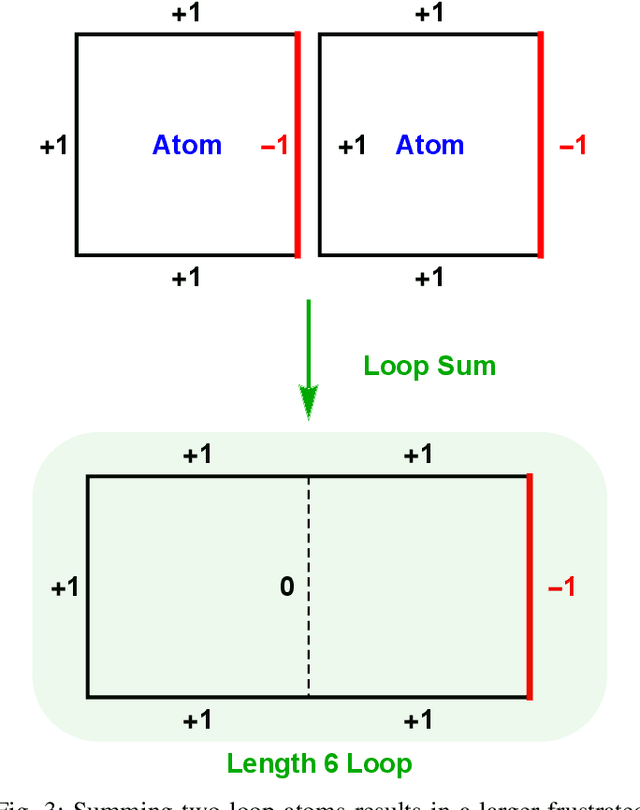
Many optimization problems can be cast into the maximum satisfiability (MAX-SAT) form, and many solvers have been developed for tackling such problems. To evaluate the performance of a MAX-SAT solver, it is convenient to generate difficult MAX-SAT instances with solutions known in advance. Here, we propose a method of generating weighted MAX-2-SAT instances inspired by the frustrated-loop algorithm used by the quantum annealing community to generate Ising spin-glass instances with nearest-neighbor coupling. Our algorithm is extended to instances whose underlying coupling graph is general, though we focus here on the case of bipartite coupling, with the associated energy being the restricted Boltzmann machine (RBM) energy. It is shown that any MAX-2-SAT problem can be reduced to the problem of minimizing an RBM energy over the nodal values. The algorithm is designed such that the difficulty of the generated instances can be tuned through a central parameter known as the frustration index. Two versions of the algorithm are presented: the random- and structured-loop algorithms. For the random-loop algorithm, we provide a thorough theoretical and empirical analysis on its mathematical properties from the perspective of frustration, and observe empirically, using simulated annealing, a double phase transition behavior in the difficulty scaling behavior driven by the frustration index. For the structured-loop algorithm, we show that it offers an improvement in difficulty of the generated instances over the random-loop algorithm, with the improvement factor scaling super-exponentially with respect to the frustration index for instances at high loop density. At the end of the paper, we provide a brief discussion of the relevance of this work to the pre-training of RBMs.

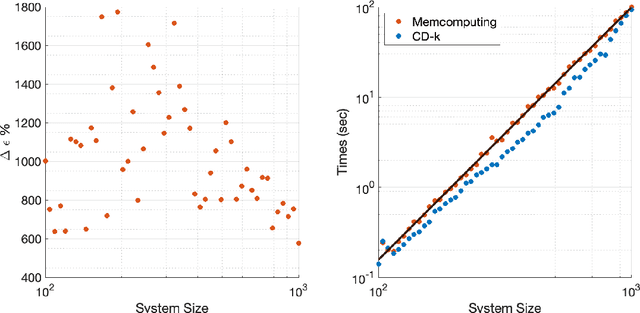
Accelerating Deep Learning with Memcomputing

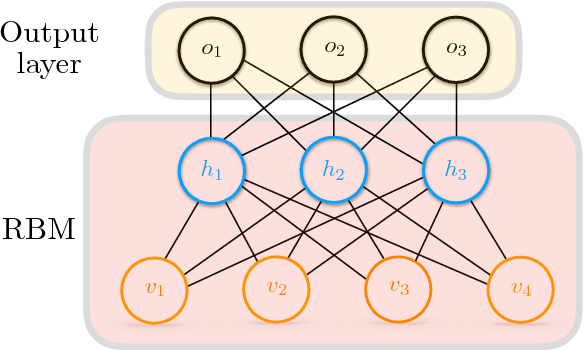
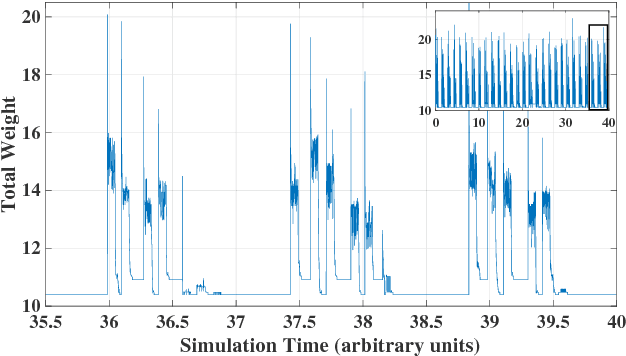
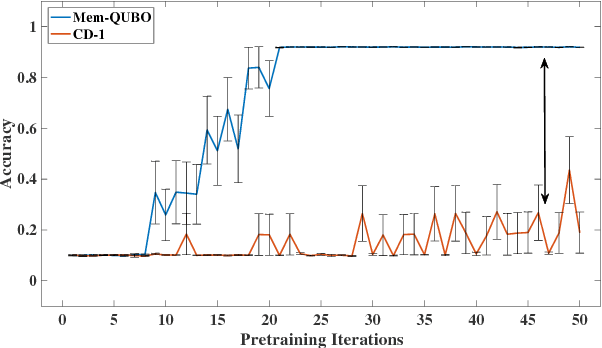
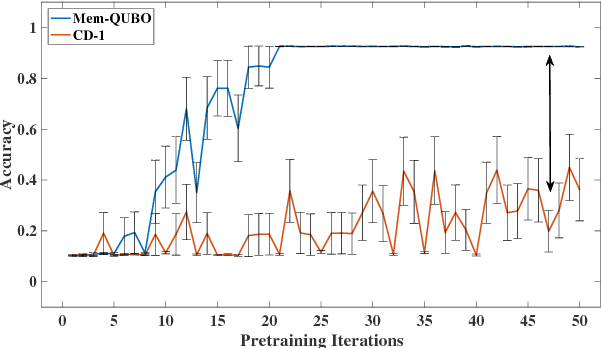
Restricted Boltzmann machines (RBMs) and their extensions, called 'deep-belief networks', are powerful neural networks that have found applications in the fields of machine learning and artificial intelligence. The standard way to training these models resorts to an iterative unsupervised procedure based on Gibbs sampling, called 'contrastive divergence' (CD), and additional supervised tuning via back-propagation. However, this procedure has been shown not to follow any gradient and can lead to suboptimal solutions. In this paper, we show an efficient alternative to CD by means of simulations of digital memcomputing machines (DMMs). We test our approach on pattern recognition using a modified version of the MNIST data set. DMMs sample effectively the vast phase space given by the model distribution of the RBM, and provide a very good approximation close to the optimum. This efficient search significantly reduces the number of pretraining iterations necessary to achieve a given level of accuracy, as well as a total performance gain over CD. In fact, the acceleration of pretraining achieved by simulating DMMs is comparable to, in number of iterations, the recently reported hardware application of the quantum annealing method on the same network and data set. Notably, however, DMMs perform far better than the reported quantum annealing results in terms of quality of the training. We also compare our method to advances in supervised training, like batch-normalization and rectifiers, that work to reduce the advantage of pretraining. We find that the memcomputing method still maintains a quality advantage ($>1\%$ in accuracy, and a $20\%$ reduction in error rate) over these approaches. Furthermore, our method is agnostic about the connectivity of the network. Therefore, it can be extended to train full Boltzmann machines, and even deep networks at once.

Memcomputing Numerical Inversion with Self-Organizing Logic Gates

We propose to use Digital Memcomputing Machines (DMMs), implemented with self-organizing logic gates (SOLGs), to solve the problem of numerical inversion. Starting from fixed-point scalar inversion we describe the generalization to solving linear systems and matrix inversion. This method, when realized in hardware, will output the result in only one computational step. As an example, we perform simulations of the scalar case using a 5-bit logic circuit made of SOLGs, and show that the circuit successfully performs the inversion. Our method can be extended efficiently to any level of precision, since we prove that producing n-bit precision in the output requires extending the circuit by at most n bits. This type of numerical inversion can be implemented by DMM units in hardware, it is scalable, and thus of great benefit to any real-time computing application.