Projective Embedding of Dynamical Systems: uniform mean field equations

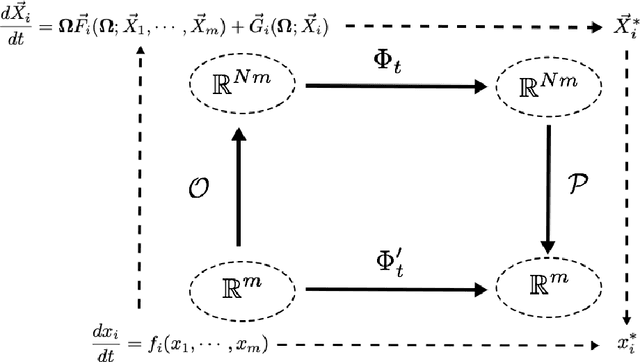
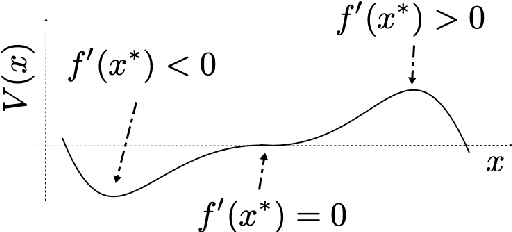
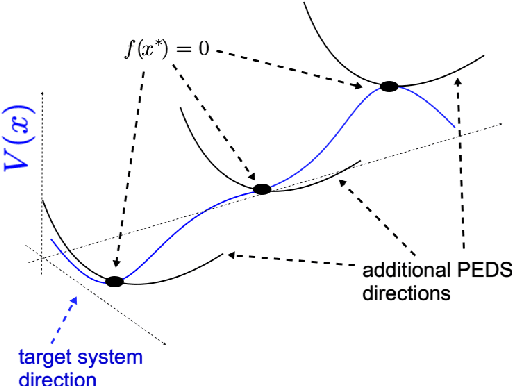
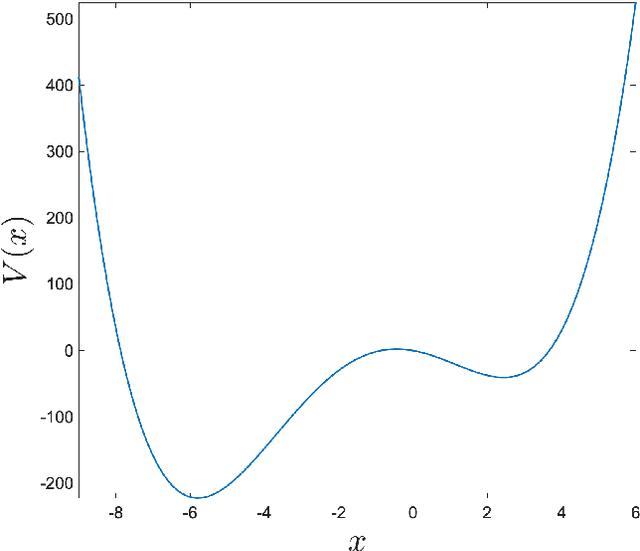
We study embeddings of continuous dynamical systems in larger dimensions via projector operators. We call this technique PEDS, projective embedding of dynamical systems, as the stable fixed point of the dynamics are recovered via projection from the higher dimensional space. In this paper we provide a general definition and prove that for a particular type of projector operator of rank-1, the uniform mean field projector, the equations of motion become a mean field approximation of the dynamical system. While in general the embedding depends on a specified variable ordering, the same is not true for the uniform mean field projector. In addition, we prove that the original stable fixed points remain stable fixed points of the dynamics, saddle points remain saddle, but unstable fixed points become saddles.

Global minimization via classical tunneling assisted by collective force field formation

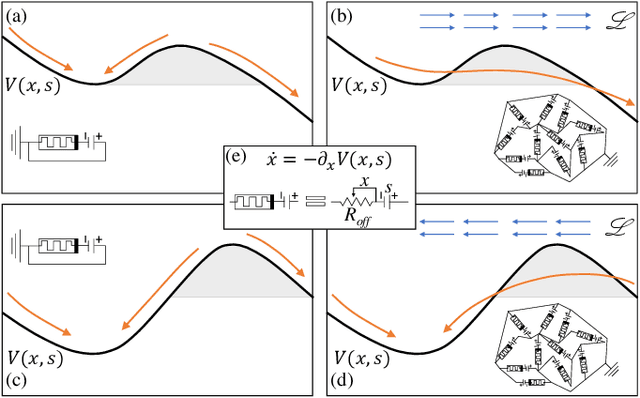
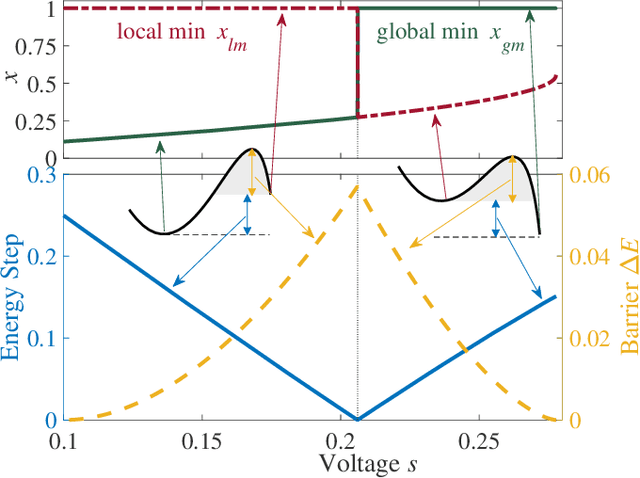
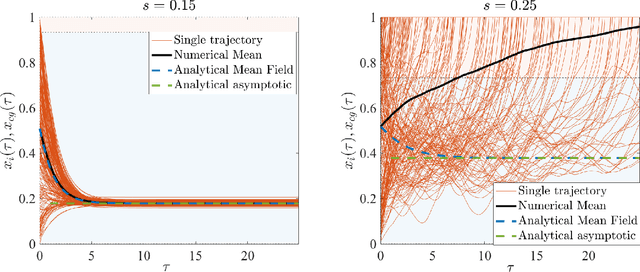
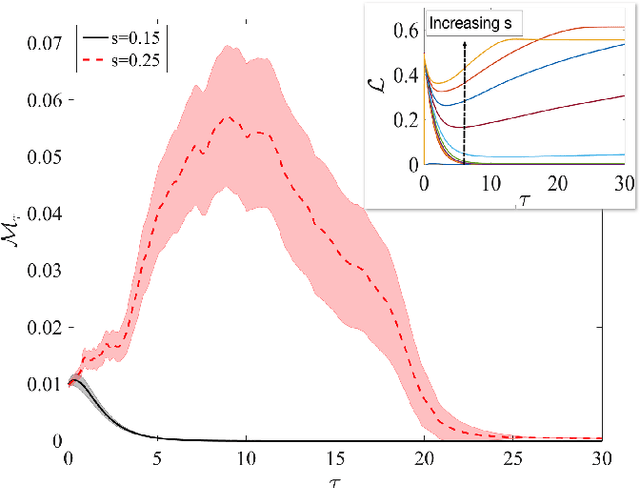
Simple dynamical models can produce intricate behaviors in large networks. These behaviors can often be observed in a wide variety of physical systems captured by the network of interactions. Here we describe a phenomenon where the increase of dimensions self-consistently generates a force field due to dynamical instabilities. This can be understood as an unstable ("rumbling") tunneling mechanism between minima in an effective potential. We dub this collective and nonperturbative effect a "Lyapunov force" which steers the system towards the global minimum of the potential function, even if the full system has a constellation of equilibrium points growing exponentially with the system size. The system we study has a simple mapping to a flow network, equivalent to current-driven memristors. The mechanism is appealing for its physical relevance in nanoscale physics, and to possible applications in optimization, novel Monte Carlo schemes and machine learning.

Accelerating Deep Learning with Memcomputing

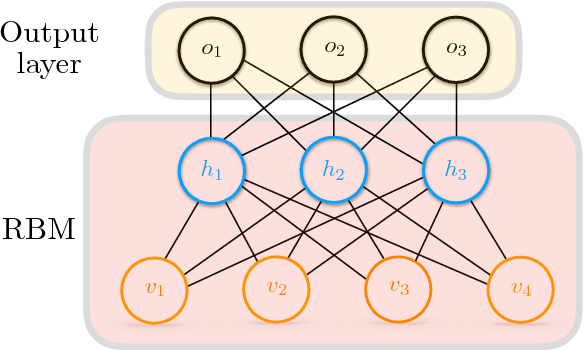
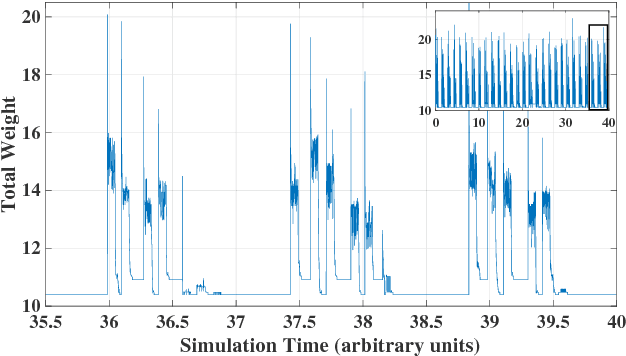
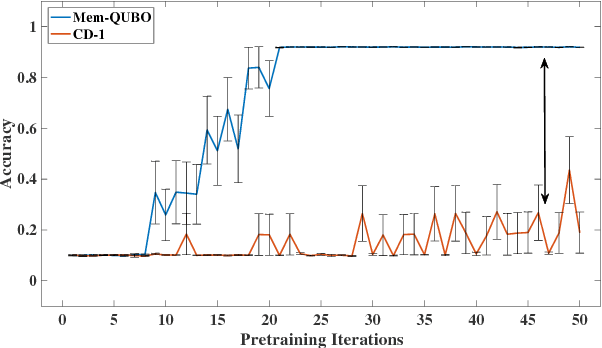
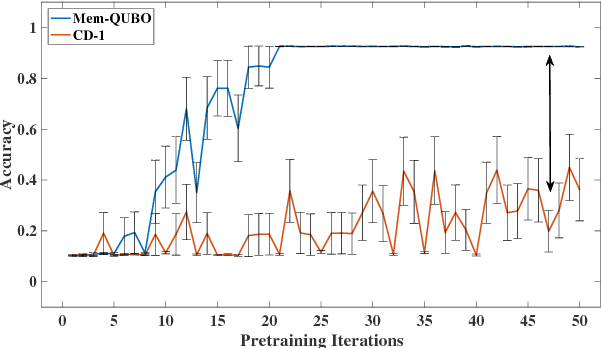
Restricted Boltzmann machines (RBMs) and their extensions, called 'deep-belief networks', are powerful neural networks that have found applications in the fields of machine learning and artificial intelligence. The standard way to training these models resorts to an iterative unsupervised procedure based on Gibbs sampling, called 'contrastive divergence' (CD), and additional supervised tuning via back-propagation. However, this procedure has been shown not to follow any gradient and can lead to suboptimal solutions. In this paper, we show an efficient alternative to CD by means of simulations of digital memcomputing machines (DMMs). We test our approach on pattern recognition using a modified version of the MNIST data set. DMMs sample effectively the vast phase space given by the model distribution of the RBM, and provide a very good approximation close to the optimum. This efficient search significantly reduces the number of pretraining iterations necessary to achieve a given level of accuracy, as well as a total performance gain over CD. In fact, the acceleration of pretraining achieved by simulating DMMs is comparable to, in number of iterations, the recently reported hardware application of the quantum annealing method on the same network and data set. Notably, however, DMMs perform far better than the reported quantum annealing results in terms of quality of the training. We also compare our method to advances in supervised training, like batch-normalization and rectifiers, that work to reduce the advantage of pretraining. We find that the memcomputing method still maintains a quality advantage ($>1\%$ in accuracy, and a $20\%$ reduction in error rate) over these approaches. Furthermore, our method is agnostic about the connectivity of the network. Therefore, it can be extended to train full Boltzmann machines, and even deep networks at once.

Memcomputing: Leveraging memory and physics to compute efficiently

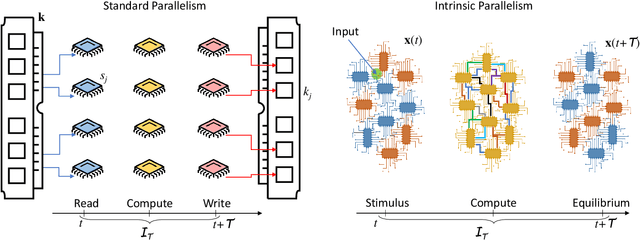
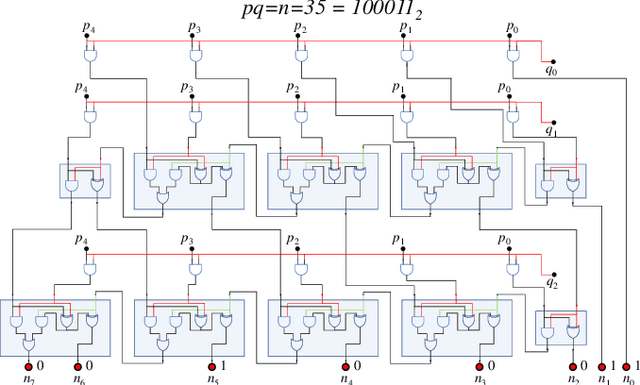
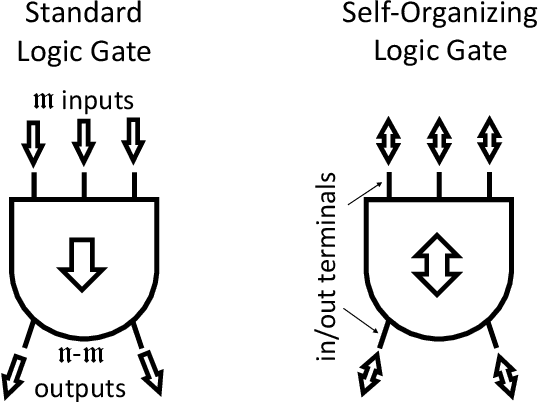
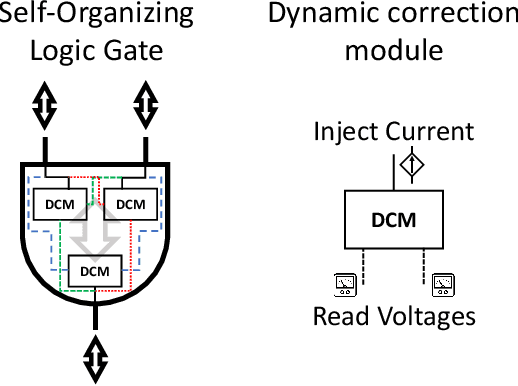
It is well known that physical phenomena may be of great help in computing some difficult problems efficiently. A typical example is prime factorization that may be solved in polynomial time by exploiting quantum entanglement on a quantum computer. There are, however, other types of (non-quantum) physical properties that one may leverage to compute efficiently a wide range of hard problems. In this perspective we discuss how to employ one such property, memory (time non-locality), in a novel physics-based approach to computation: Memcomputing. In particular, we focus on digital memcomputing machines (DMMs) that are scalable. DMMs can be realized with non-linear dynamical systems with memory. The latter property allows the realization of a new type of Boolean logic, one that is self-organizing. Self-organizing logic gates are "terminal-agnostic", namely they do not distinguish between input and output terminals. When appropriately assembled to represent a given combinatorial/optimization problem, the corresponding self-organizing circuit converges to the equilibrium points that express the solutions of the problem at hand. In doing so, DMMs take advantage of the long-range order that develops during the transient dynamics. This collective dynamical behavior, reminiscent of a phase transition, or even the "edge of chaos", is mediated by families of classical trajectories (instantons) that connect critical points of increasing stability in the system's phase space. The topological character of the solution search renders DMMs robust against noise and structural disorder. Since DMMs are non-quantum systems described by ordinary differential equations, not only can they be built in hardware with available technology, they can also be simulated efficiently on modern classical computers. As an example, we will show the polynomial-time solution of the subset-sum problem for the worst...

On the Universality of Memcomputing Machines

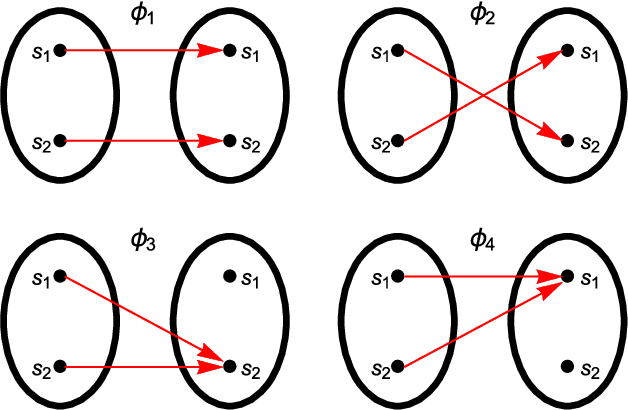
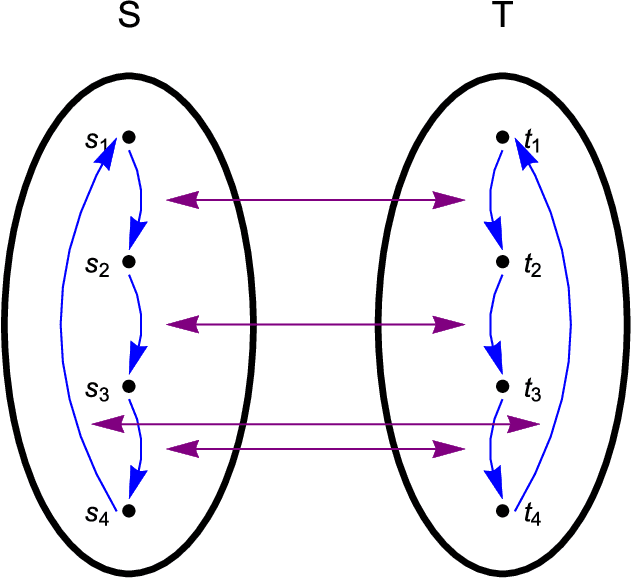
Universal memcomputing machines (UMMs) [IEEE Trans. Neural Netw. Learn. Syst. 26, 2702 (2015)] represent a novel computational model in which memory (time non-locality) accomplishes both tasks of storing and processing of information. UMMs have been shown to be Turing-complete, namely they can simulate any Turing machine. In this paper, using set theory and cardinality arguments, we compare them with liquid-state machines (or "reservoir computing") and quantum machines ("quantum computing"). We show that UMMs can simulate both types of machines, hence they are both "liquid-" or "reservoir-complete" and "quantum-complete". Of course, these statements pertain only to the type of problems these machines can solve, and not to the amount of resources required for such simulations. Nonetheless, the method presented here provides a general framework in which to describe the relation between UMMs and any other type of computational model.

Evidence of an exponential speed-up in the solution of hard optimization problems

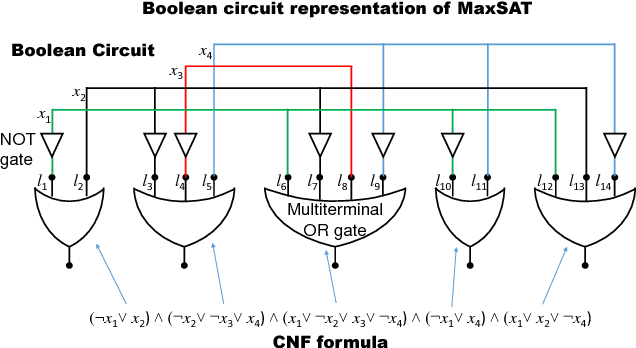
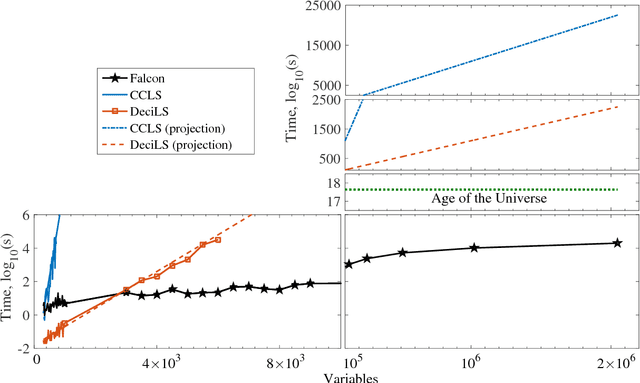
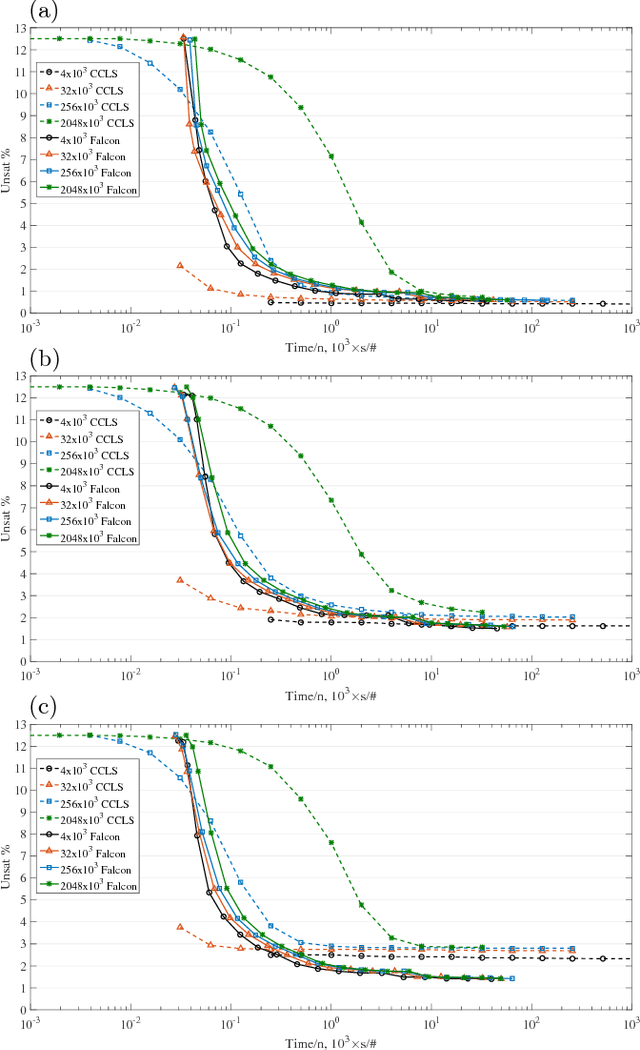
Optimization problems pervade essentially every scientific discipline and industry. Many such problems require finding a solution that maximizes the number of constraints satisfied. Often, these problems are particularly difficult to solve because they belong to the NP-hard class, namely algorithms that always find a solution in polynomial time are not known. Over the past decades, research has focused on developing heuristic approaches that attempt to find an approximation to the solution. However, despite numerous research efforts, in many cases even approximations to the optimal solution are hard to find, as the computational time for further refining a candidate solution grows exponentially with input size. Here, we show a non-combinatorial approach to hard optimization problems that achieves an exponential speed-up and finds better approximations than the current state-of-the-art. First, we map the optimization problem into a boolean circuit made of specially designed, self-organizing logic gates, which can be built with (non-quantum) electronic components; the equilibrium points of the circuit represent the approximation to the problem at hand. Then, we solve its associated non-linear ordinary differential equations numerically, towards the equilibrium points. We demonstrate this exponential gain by comparing a sequential MatLab implementation of our solver with the winners of the 2016 Max-SAT competition on a variety of hard optimization instances. We show empirical evidence that our solver scales linearly with the size of the problem, both in time and memory, and argue that this property derives from the collective behavior of the simulated physical circuit. Our approach can be applied to other types of optimization problems and the results presented here have far-reaching consequences in many fields.

Memcomputing Numerical Inversion with Self-Organizing Logic Gates

We propose to use Digital Memcomputing Machines (DMMs), implemented with self-organizing logic gates (SOLGs), to solve the problem of numerical inversion. Starting from fixed-point scalar inversion we describe the generalization to solving linear systems and matrix inversion. This method, when realized in hardware, will output the result in only one computational step. As an example, we perform simulations of the scalar case using a 5-bit logic circuit made of SOLGs, and show that the circuit successfully performs the inversion. Our method can be extended efficiently to any level of precision, since we prove that producing n-bit precision in the output requires extending the circuit by at most n bits. This type of numerical inversion can be implemented by DMM units in hardware, it is scalable, and thus of great benefit to any real-time computing application.

Memcomputing NP-complete problems in polynomial time using polynomial resources and collective states

Memcomputing is a novel non-Turing paradigm of computation that uses interacting memory cells (memprocessors for short) to store and process information on the same physical platform. It was recently proved mathematically that memcomputing machines have the same computational power of non-deterministic Turing machines. Therefore, they can solve NP-complete problems in polynomial time and, using the appropriate architecture, with resources that only grow polynomially with the input size. The reason for this computational power stems from properties inspired by the brain and shared by any universal memcomputing machine, in particular intrinsic parallelism and information overhead, namely the capability of compressing information in the collective state of the memprocessor network. Here, we show an experimental demonstration of an actual memcomputing architecture that solves the NP-complete version of the subset-sum problem in only one step and is composed of a number of memprocessors that scales linearly with the size of the problem. We have fabricated this architecture using standard microelectronic technology so that it can be easily realized in any laboratory setting. Even though the particular machine presented here is eventually limited by noise--and will thus require error-correcting codes to scale to an arbitrary number of memprocessors--it represents the first proof-of-concept of a machine capable of working with the collective state of interacting memory cells, unlike the present-day single-state machines built using the von Neumann architecture.

Memcomputing with membrane memcapacitive systems

We show theoretically that networks of membrane memcapacitive systems -- capacitors with memory made out of membrane materials -- can be used to perform a complete set of logic gates in a massively parallel way by simply changing the external input amplitudes, but not the topology of the network. This polymorphism is an important characteristic of memcomputing (computing with memories) that closely reproduces one of the main features of the brain. A practical realization of these membrane memcapacitive systems, using, e.g., graphene or other 2D materials, would be a step forward towards a solid-state realization of memcomputing with passive devices.

Universal Memcomputing Machines

We introduce the notion of universal memcomputing machines (UMMs): a class of brain-inspired general-purpose computing machines based on systems with memory, whereby processing and storing of information occur on the same physical location. We analytically prove that the memory properties of UMMs endow them with universal computing power - they are Turing-complete -, intrinsic parallelism, functional polymorphism, and information overhead, namely their collective states can support exponential data compression directly in memory. We also demonstrate that a UMM has the same computational power as a non-deterministic Turing machine, namely it can solve NP--complete problems in polynomial time. However, by virtue of its information overhead, a UMM needs only an amount of memory cells (memprocessors) that grows polynomially with the problem size. As an example we provide the polynomial-time solution of the subset-sum problem and a simple hardware implementation of the same. Even though these results do not prove the statement NP=P within the Turing paradigm, the practical realization of these UMMs would represent a paradigm shift from present von Neumann architectures bringing us closer to brain-like neural computation.