On the Universality of Memcomputing Machines
Paper and Code
Dec 23, 2017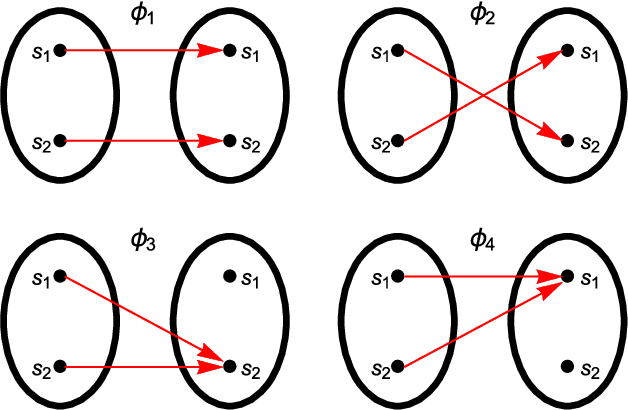
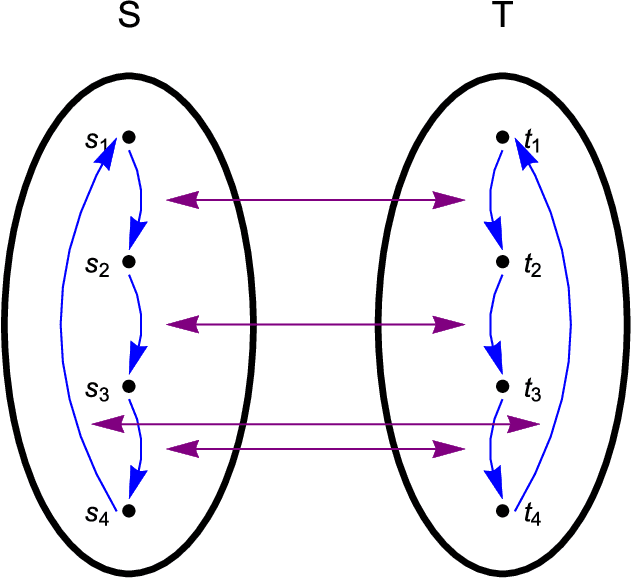
Universal memcomputing machines (UMMs) [IEEE Trans. Neural Netw. Learn. Syst. 26, 2702 (2015)] represent a novel computational model in which memory (time non-locality) accomplishes both tasks of storing and processing of information. UMMs have been shown to be Turing-complete, namely they can simulate any Turing machine. In this paper, using set theory and cardinality arguments, we compare them with liquid-state machines (or "reservoir computing") and quantum machines ("quantum computing"). We show that UMMs can simulate both types of machines, hence they are both "liquid-" or "reservoir-complete" and "quantum-complete". Of course, these statements pertain only to the type of problems these machines can solve, and not to the amount of resources required for such simulations. Nonetheless, the method presented here provides a general framework in which to describe the relation between UMMs and any other type of computational model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge