Global minimization via classical tunneling assisted by collective force field formation

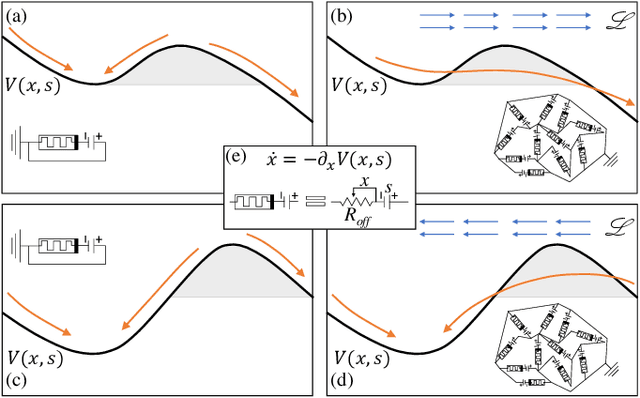
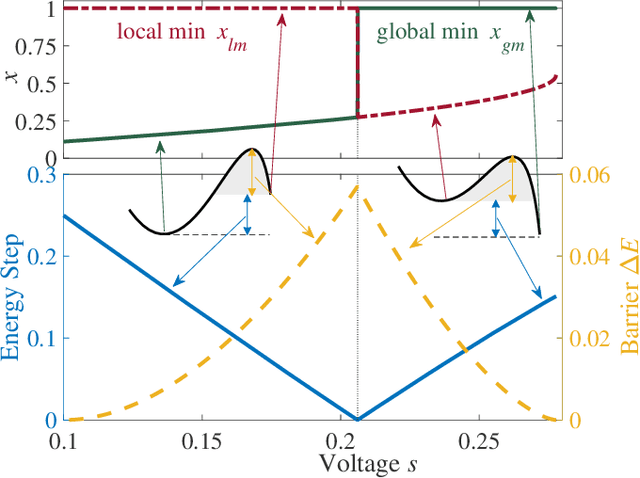
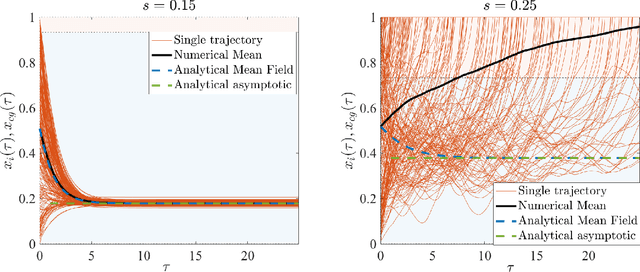
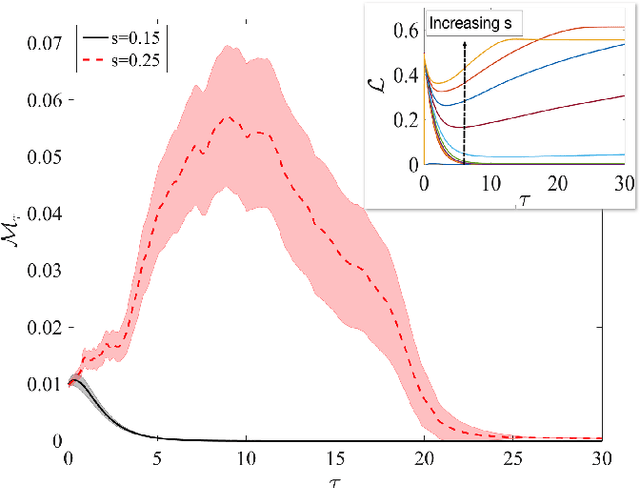
Simple dynamical models can produce intricate behaviors in large networks. These behaviors can often be observed in a wide variety of physical systems captured by the network of interactions. Here we describe a phenomenon where the increase of dimensions self-consistently generates a force field due to dynamical instabilities. This can be understood as an unstable ("rumbling") tunneling mechanism between minima in an effective potential. We dub this collective and nonperturbative effect a "Lyapunov force" which steers the system towards the global minimum of the potential function, even if the full system has a constellation of equilibrium points growing exponentially with the system size. The system we study has a simple mapping to a flow network, equivalent to current-driven memristors. The mechanism is appealing for its physical relevance in nanoscale physics, and to possible applications in optimization, novel Monte Carlo schemes and machine learning.

The Computational Capacity of Memristor Reservoirs

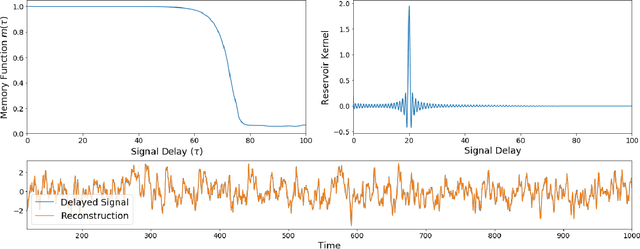
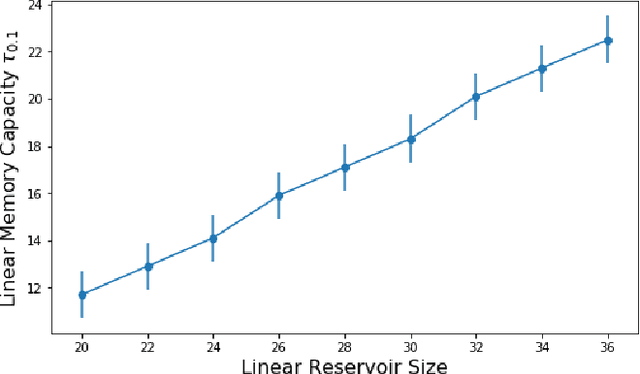
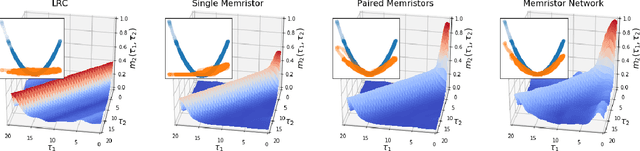
Reservoir computing is a machine learning paradigm in which a high-dimensional dynamical system, or \emph{reservoir}, is used to approximate and perform predictions on time series data. Its simple training procedure allows for very large reservoirs that can provide powerful computational capabilities. The scale, speed and power-usage characteristics of reservoir computing could be enhanced by constructing reservoirs out of electronic circuits, but this requires a precise understanding of how such circuits process and store information. We analyze the feasibility and optimal design of such reservoirs by considering the equations of motion of circuits that include both linear elements (resistors, inductors, and capacitors) and nonlinear memory elements (called memristors). This complements previous studies, which have examined such systems through simulation and experiment. We provide analytic results regarding the fundamental feasibility of such reservoirs, and give a systematic characterization of their computational properties, examining the types of input-output relationships that may be approximated. This allows us to design reservoirs with optimal properties in terms of their ability to reconstruct a certain signal (or functions thereof). In particular, by introducing measures of the total linear and nonlinear computational capacities of the reservoir, we are able to design electronic circuits whose total computation capacity scales linearly with the system size. Comparison with conventional echo state reservoirs show that these electronic reservoirs can match or exceed their performance in a form that may be directly implemented in hardware.