Partial information decomposition as information bottleneck

The partial information decomposition (PID) aims to quantify the amount of redundant information that a set of sources provide about a target. Here we show that this goal can be formulated as a type of information bottleneck (IB) problem, which we term the "redundancy bottleneck" (RB). The RB formalizes a tradeoff between prediction and compression: it extracts information from the sources that predicts the target, without revealing which source provided the information. It can be understood as a generalization "Blackwell redundancy", which we previously proposed as a principled measure of PID redundancy. The "RB curve" quantifies the prediction/compression tradeoff at multiple scales. This curve can also be quantified for individual sources, allowing subsets of redundant sources to be identified without combinatorial optimization. We provide an efficient iterative algorithm for computing the RB curve.

The Computational Capacity of Memristor Reservoirs

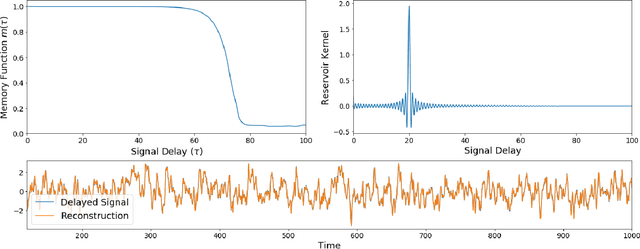
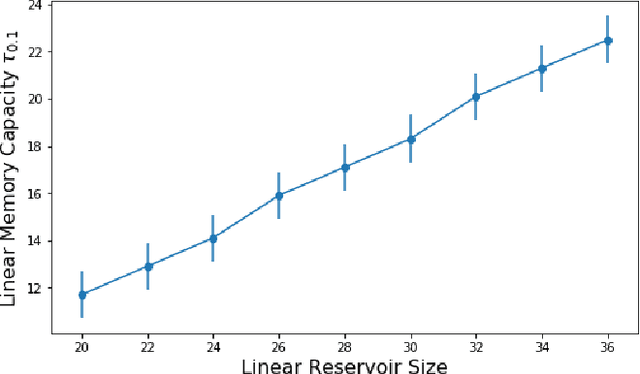
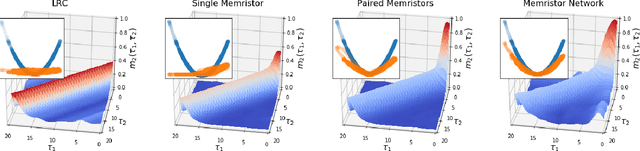
Reservoir computing is a machine learning paradigm in which a high-dimensional dynamical system, or \emph{reservoir}, is used to approximate and perform predictions on time series data. Its simple training procedure allows for very large reservoirs that can provide powerful computational capabilities. The scale, speed and power-usage characteristics of reservoir computing could be enhanced by constructing reservoirs out of electronic circuits, but this requires a precise understanding of how such circuits process and store information. We analyze the feasibility and optimal design of such reservoirs by considering the equations of motion of circuits that include both linear elements (resistors, inductors, and capacitors) and nonlinear memory elements (called memristors). This complements previous studies, which have examined such systems through simulation and experiment. We provide analytic results regarding the fundamental feasibility of such reservoirs, and give a systematic characterization of their computational properties, examining the types of input-output relationships that may be approximated. This allows us to design reservoirs with optimal properties in terms of their ability to reconstruct a certain signal (or functions thereof). In particular, by introducing measures of the total linear and nonlinear computational capacities of the reservoir, we are able to design electronic circuits whose total computation capacity scales linearly with the system size. Comparison with conventional echo state reservoirs show that these electronic reservoirs can match or exceed their performance in a form that may be directly implemented in hardware.

A novel approach to multivariate redundancy and synergy

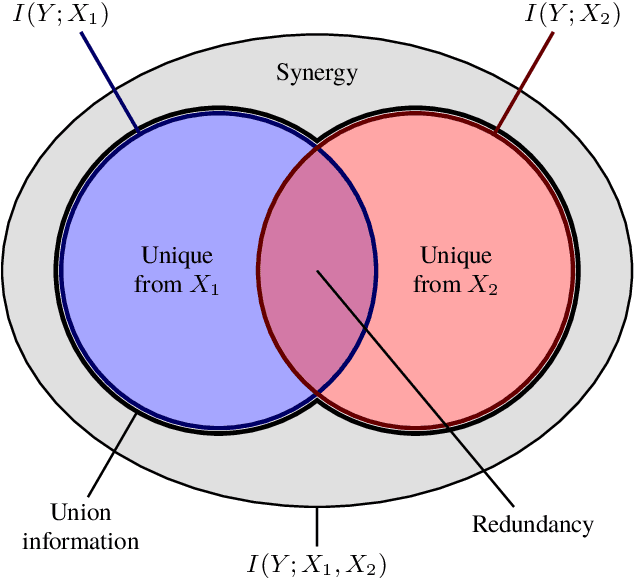
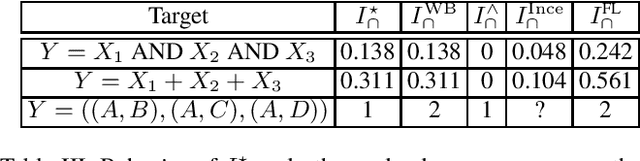
Consider a situation in which a set of $n$ "source" random variables $X_{1},\dots,X_{n}$ have information about some "target" random variable $Y$. For example, in neuroscience $Y$ might represent the state of an external stimulus and $X_{1},\dots,X_{n}$ the activity of $n$ different brain regions. Recent work in information theory has considered how to decompose the information that the sources $X_{1},\dots,X_{n}$ provide about the target $Y$ into separate terms such as (1) the "redundant information" that is shared among all of sources, (2) the "unique information" that is provided only by a single source, (3) the "synergistic information" that is provided by all sources only when considered jointly, and (4) the "union information" that is provided by at least one source. We propose a novel framework deriving such a decomposition that can be applied to any number of sources. Our measures are motivated in three distinct ways: via a formal analogy to intersection and union operators in set theory, via a decision-theoretic operationalization based on Blackwell's theorem, and via an axiomatic derivation. A key aspect of our approach is that we relax the assumption that measures of redundancy and union information should be related by the inclusion-exclusion principle. We discuss relations to previous proposals as well as possible generalizations.

Decomposing information into copying versus transformation

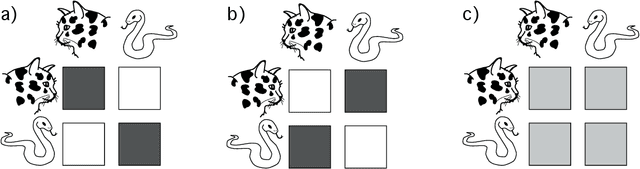
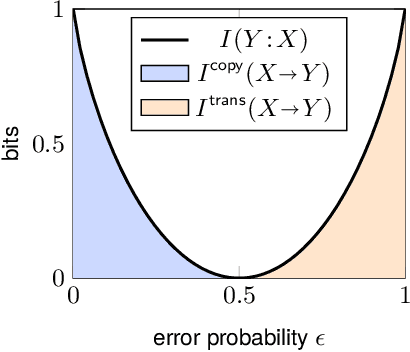
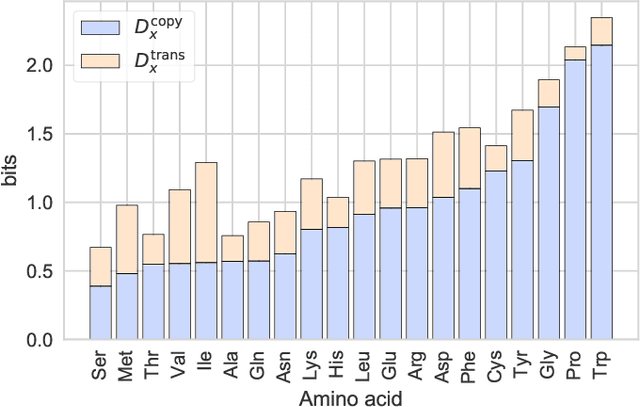
In many real-world systems, information can be transmitted in two qualitatively different ways: by {\em copying} or by {\em transformation}. {\em Copying} occurs when messages are transmitted without modification, for example when an offspring receives an unaltered copy of a gene from its parent. {\em Transformation} occurs when messages are modified in a systematic way during transmission, e.g., when non-random mutations occur during biological reproduction. Standard information-theoretic measures of information transmission, such as mutual information, do not distinguish these two modes of information transfer, even though they may reflect different mechanisms and have different functional consequences. We propose a decomposition of mutual information which separately quantifies the information transmitted by copying versus the information transmitted by transformation. Our measures of copy and transformation information are derived from a few simple axioms, and have natural operationalizations in terms of hypothesis testing and thermodynamics. In this later case, we show that our measure of copy information corresponds to the minimal amount of work needed by a physical copying process, having special relevance for the physics of replication of biological information. We demonstrate our measures on a real world dataset of amino acid substitution rates. Our decomposition into copy and transformation information is general and applies to any system in which the fidelity of copying, rather than simple predictability, is of critical relevance.

Nonlinear Information Bottleneck

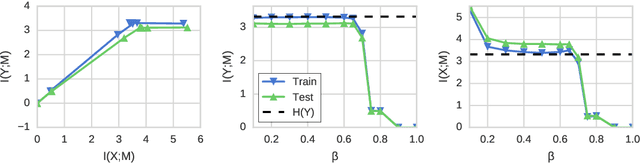
Information bottleneck [IB] is a technique for extracting information in some `input' random variable that is relevant for predicting some different 'output' random variable. IB works by encoding the input in a compressed 'bottleneck variable' from which the output can then be accurately decoded. IB can be difficult to compute in practice, and has been mainly developed for two limited cases: (1) discrete random variables with small state spaces, and (2) continuous random variables that are jointly Gaussian distributed (in which case the encoding and decoding maps are linear). We propose a method to perform IB in more general domains. Our approach can be applied to discrete or continuous inputs and outputs, and allows for nonlinear encoding and decoding maps. The method uses a novel upper bound on the IB objective, derived using a non-parametric estimator of mutual information and a variational approximation. We show how to implement the method using neural networks and gradient-based optimization, and demonstrate its performance on the MNIST dataset.

Pathologies in information bottleneck for deterministic supervised learning

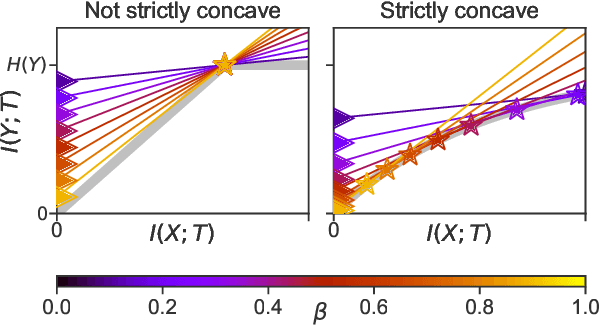
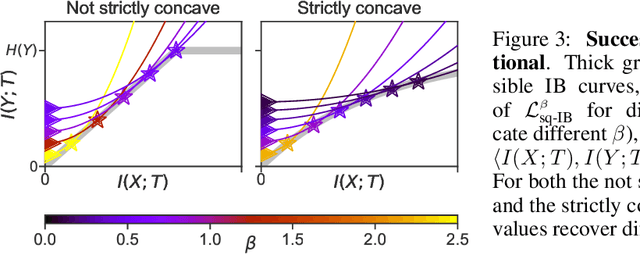
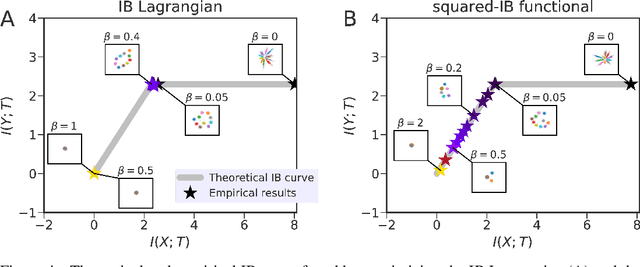
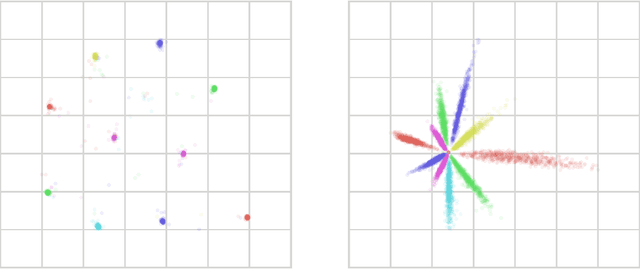
Information bottleneck (IB) is a method for extracting information from one random variable $X$ that is relevant for predicting another random variable $Y$. To do so, IB identifies an intermediate "bottleneck" variable $T$ that has low mutual information $I(X;T)$ and high mutual information $I(Y;T)$. The "IB curve" characterizes the set of bottleneck variables that achieve maximal $I(Y;T)$ for a given $I(X;T)$, and is typically explored by optimizing the "IB Lagrangian", $I(Y;T) - \beta I(X;T)$. Recently, there has been interest in applying IB to supervised learning, particularly for classification problems that use neural networks. In most classification problems, the output class $Y$ is a deterministic function of the input $X$, which we refer to as "deterministic supervised learning". We demonstrate three pathologies that arise when IB is used in any scenario where $Y$ is a deterministic function of $X$: (1) the IB curve cannot be recovered by optimizing the IB Lagrangian for different values of $\beta$; (2) there are "uninteresting" solutions at all points of the IB curve; and (3) for classifiers that achieve low error rates, the activity of different hidden layers will not exhibit a strict trade-off between compression and prediction, contrary to a recent proposal. To address problem (1), we propose a functional that, unlike the IB Lagrangian, can recover the IB curve in all cases. We finish by demonstrating these issues on the MNIST dataset.

Estimating Mixture Entropy with Pairwise Distances

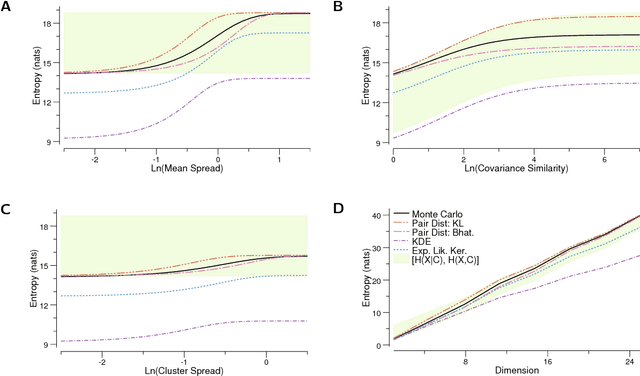
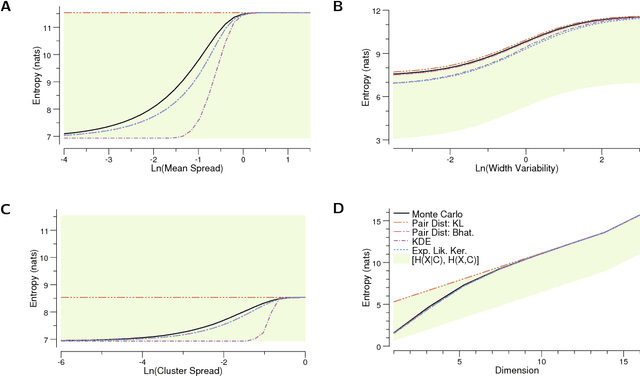
Mixture distributions arise in many parametric and non-parametric settings -- for example, in Gaussian mixture models and in non-parametric estimation. It is often necessary to compute the entropy of a mixture, but, in most cases, this quantity has no closed-form expression, making some form of approximation necessary. We propose a family of estimators based on a pairwise distance function between mixture components, and show that this estimator class has many attractive properties. For many distributions of interest, the proposed estimators are efficient to compute, differentiable in the mixture parameters, and become exact when the mixture components are clustered. We prove this family includes lower and upper bounds on the mixture entropy. The Chernoff $\alpha$-divergence gives a lower bound when chosen as the distance function, with the Bhattacharyya distance providing the tightest lower bound for components that are symmetric and members of a location family. The Kullback-Leibler divergence gives an upper bound when used as the distance function. We provide closed-form expressions of these bounds for mixtures of Gaussians, and discuss their applications to the estimation of mutual information. We then demonstrate that our bounds are significantly tighter than well-known existing bounds using numeric simulations. This estimator class is very useful in optimization problems involving maximization/minimization of entropy and mutual information, such as MaxEnt and rate distortion problems.

The Minor Fall, the Major Lift: Inferring Emotional Valence of Musical Chords through Lyrics

We investigate the association between musical chords and lyrics by analyzing a large dataset of user-contributed guitar tablatures. Motivated by the idea that the emotional content of chords is reflected in the words used in corresponding lyrics, we analyze associations between lyrics and chord categories. We also examine the usage patterns of chords and lyrics in different musical genres, historical eras, and geographical regions. Our overall results confirms a previously known association between Major chords and positive valence. We also report a wide variation in this association across regions, genres, and eras. Our results suggest possible existence of different emotional associations for other types of chords.

Extraction of Pharmacokinetic Evidence of Drug-drug Interactions from the Literature

Drug-drug interaction (DDI) is a major cause of morbidity and mortality and a subject of intense scientific interest. Biomedical literature mining can aid DDI research by extracting evidence for large numbers of potential interactions from published literature and clinical databases. Though DDI is investigated in domains ranging in scale from intracellular biochemistry to human populations, literature mining has not been used to extract specific types of experimental evidence, which are reported differently for distinct experimental goals. We focus on pharmacokinetic evidence for DDI, essential for identifying causal mechanisms of putative interactions and as input for further pharmacological and pharmaco-epidemiology investigations. We used manually curated corpora of PubMed abstracts and annotated sentences to evaluate the efficacy of literature mining on two tasks: first, identifying PubMed abstracts containing pharmacokinetic evidence of DDIs; second, extracting sentences containing such evidence from abstracts. We implemented a text mining pipeline and evaluated it using several linear classifiers and a variety of feature transforms. The most important textual features in the abstract and sentence classification tasks were analyzed. We also investigated the performance benefits of using features derived from PubMed metadata fields, various publicly available named entity recognizers, and pharmacokinetic dictionaries. Several classifiers performed very well in distinguishing relevant and irrelevant abstracts (reaching F1~=0.93, MCC~=0.74, iAUC~=0.99) and sentences (F1~=0.76, MCC~=0.65, iAUC~=0.83). We found that word bigram features were important for achieving optimal classifier performance and that features derived from Medical Subject Headings (MeSH) terms significantly improved abstract classification. ...

Prediction and Modularity in Dynamical Systems

Identifying and understanding modular organizations is centrally important in the study of complex systems. Several approaches to this problem have been advanced, many framed in information-theoretic terms. Our treatment starts from the complementary point of view of statistical modeling and prediction of dynamical systems. It is known that for finite amounts of training data, simpler models can have greater predictive power than more complex ones. We use the trade-off between model simplicity and predictive accuracy to generate optimal multiscale decompositions of dynamical networks into weakly-coupled, simple modules. State-dependent and causal versions of our method are also proposed.