A novel approach to multivariate redundancy and synergy

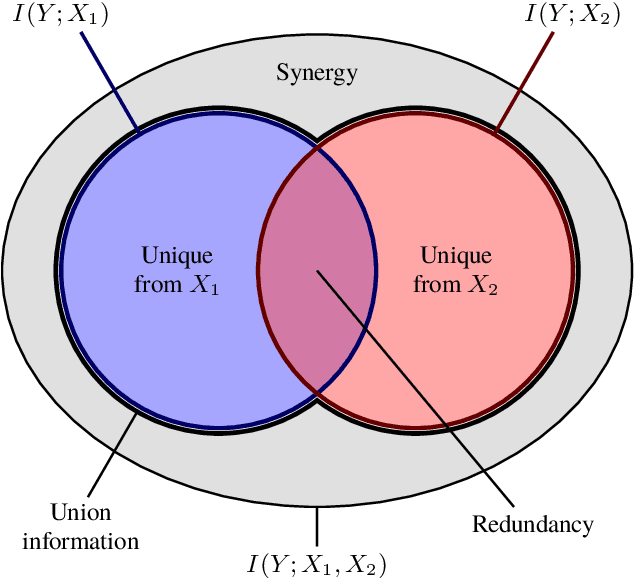
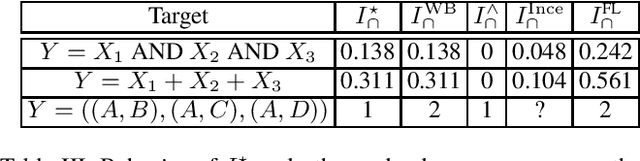
Consider a situation in which a set of $n$ "source" random variables $X_{1},\dots,X_{n}$ have information about some "target" random variable $Y$. For example, in neuroscience $Y$ might represent the state of an external stimulus and $X_{1},\dots,X_{n}$ the activity of $n$ different brain regions. Recent work in information theory has considered how to decompose the information that the sources $X_{1},\dots,X_{n}$ provide about the target $Y$ into separate terms such as (1) the "redundant information" that is shared among all of sources, (2) the "unique information" that is provided only by a single source, (3) the "synergistic information" that is provided by all sources only when considered jointly, and (4) the "union information" that is provided by at least one source. We propose a novel framework deriving such a decomposition that can be applied to any number of sources. Our measures are motivated in three distinct ways: via a formal analogy to intersection and union operators in set theory, via a decision-theoretic operationalization based on Blackwell's theorem, and via an axiomatic derivation. A key aspect of our approach is that we relax the assumption that measures of redundancy and union information should be related by the inclusion-exclusion principle. We discuss relations to previous proposals as well as possible generalizations.