Michele Bonnin
Projective Embedding of Dynamical Systems: uniform mean field equations
Jan 07, 2022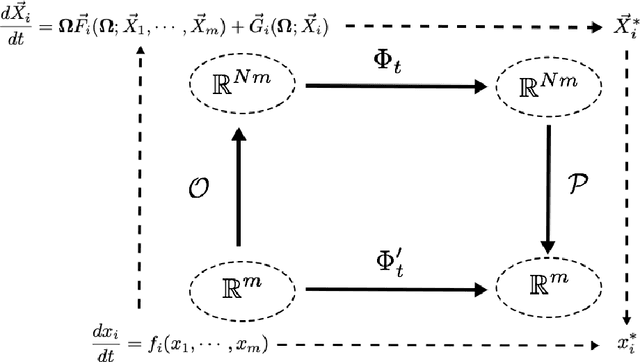
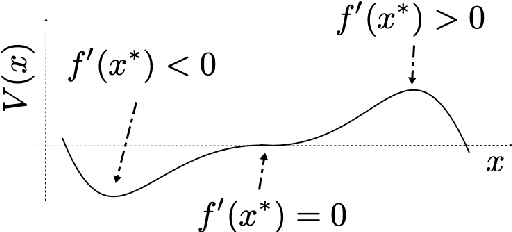
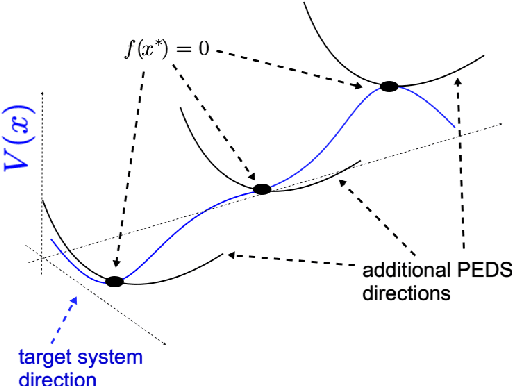
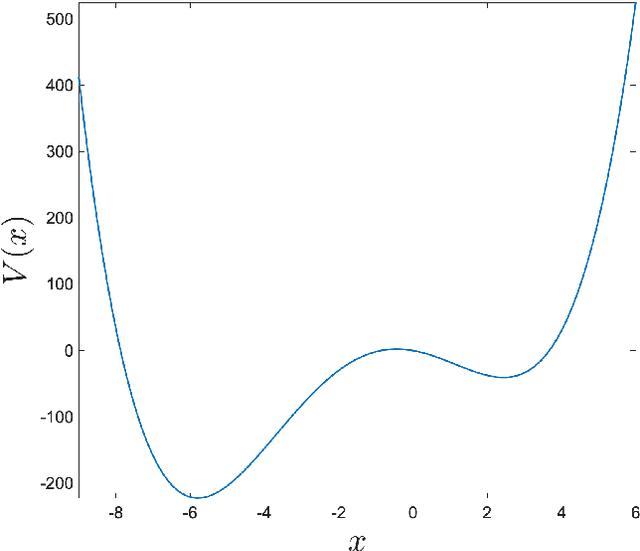
Abstract:We study embeddings of continuous dynamical systems in larger dimensions via projector operators. We call this technique PEDS, projective embedding of dynamical systems, as the stable fixed point of the dynamics are recovered via projection from the higher dimensional space. In this paper we provide a general definition and prove that for a particular type of projector operator of rank-1, the uniform mean field projector, the equations of motion become a mean field approximation of the dynamical system. While in general the embedding depends on a specified variable ordering, the same is not true for the uniform mean field projector. In addition, we prove that the original stable fixed points remain stable fixed points of the dynamics, saddle points remain saddle, but unstable fixed points become saddles.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge