Projective Embedding of Dynamical Systems: uniform mean field equations

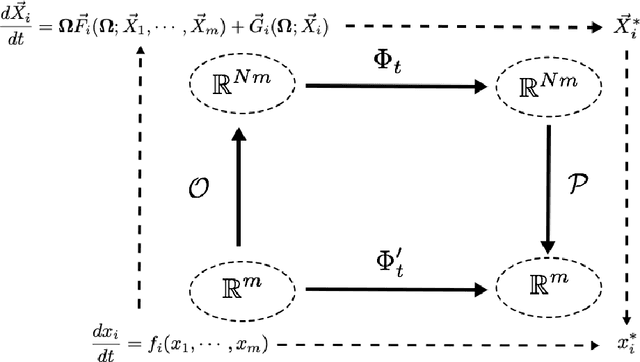
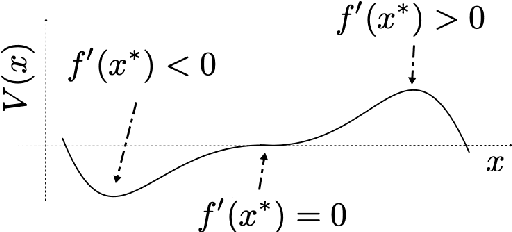
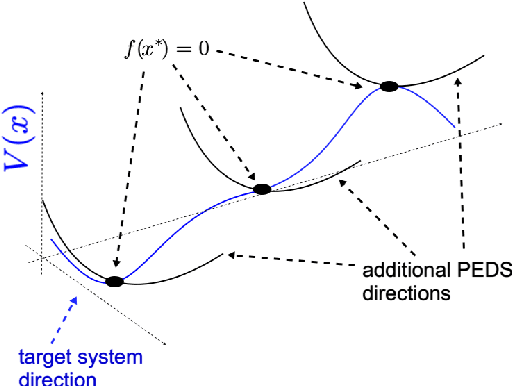
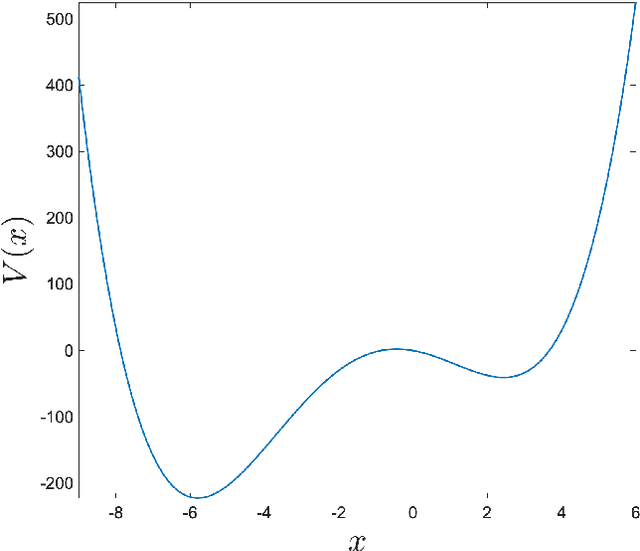
We study embeddings of continuous dynamical systems in larger dimensions via projector operators. We call this technique PEDS, projective embedding of dynamical systems, as the stable fixed point of the dynamics are recovered via projection from the higher dimensional space. In this paper we provide a general definition and prove that for a particular type of projector operator of rank-1, the uniform mean field projector, the equations of motion become a mean field approximation of the dynamical system. While in general the embedding depends on a specified variable ordering, the same is not true for the uniform mean field projector. In addition, we prove that the original stable fixed points remain stable fixed points of the dynamics, saddle points remain saddle, but unstable fixed points become saddles.

Memcomputing NP-complete problems in polynomial time using polynomial resources and collective states

Memcomputing is a novel non-Turing paradigm of computation that uses interacting memory cells (memprocessors for short) to store and process information on the same physical platform. It was recently proved mathematically that memcomputing machines have the same computational power of non-deterministic Turing machines. Therefore, they can solve NP-complete problems in polynomial time and, using the appropriate architecture, with resources that only grow polynomially with the input size. The reason for this computational power stems from properties inspired by the brain and shared by any universal memcomputing machine, in particular intrinsic parallelism and information overhead, namely the capability of compressing information in the collective state of the memprocessor network. Here, we show an experimental demonstration of an actual memcomputing architecture that solves the NP-complete version of the subset-sum problem in only one step and is composed of a number of memprocessors that scales linearly with the size of the problem. We have fabricated this architecture using standard microelectronic technology so that it can be easily realized in any laboratory setting. Even though the particular machine presented here is eventually limited by noise--and will thus require error-correcting codes to scale to an arbitrary number of memprocessors--it represents the first proof-of-concept of a machine capable of working with the collective state of interacting memory cells, unlike the present-day single-state machines built using the von Neumann architecture.