Quantum Inception Score

Motivated by the great success of classical generative models in machine learning, enthusiastic exploration of their quantum version has recently started. To depart on this journey, it is important to develop a relevant metric to evaluate the quality of quantum generative models; in the classical case, one such examples is the inception score. In this paper, we propose the quantum inception score, which relates the quality to the classical capacity of the quantum channel that classifies a given dataset. We prove that, under this proposed measure, the quantum generative models provide better quality than their classical counterparts because of the presence of quantum coherence and entanglement. Finally, we harness the quantum fluctuation theorem to characterize the physical limitation of the quality of quantum generative models.

Inference-Based Quantum Sensing

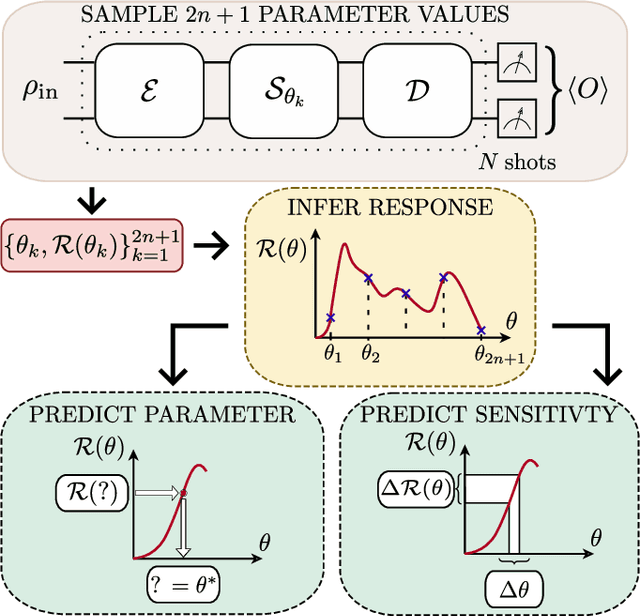
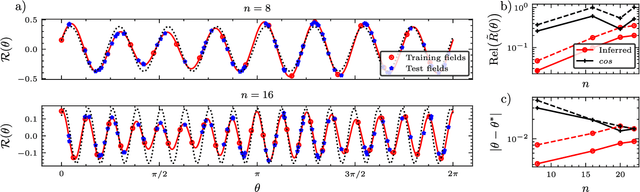
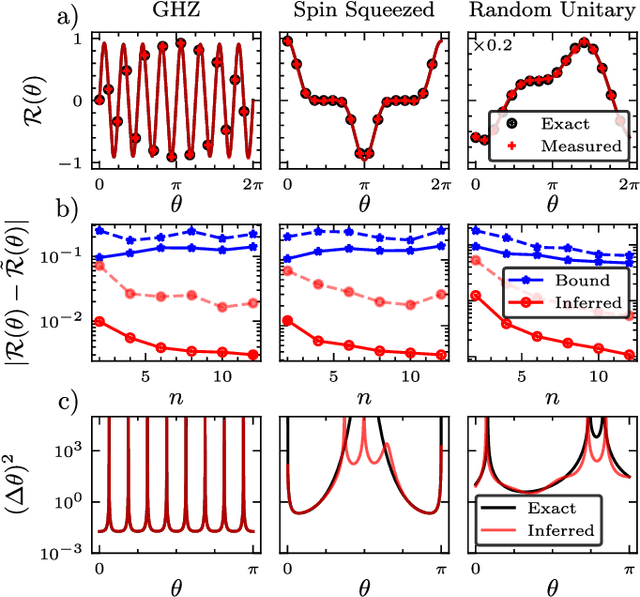
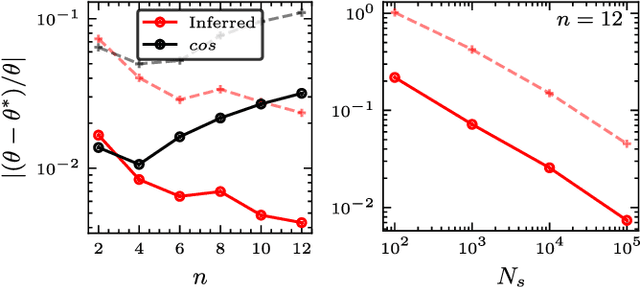
In a standard Quantum Sensing (QS) task one aims at estimating an unknown parameter $\theta$, encoded into an $n$-qubit probe state, via measurements of the system. The success of this task hinges on the ability to correlate changes in the parameter to changes in the system response $\mathcal{R}(\theta)$ (i.e., changes in the measurement outcomes). For simple cases the form of $\mathcal{R}(\theta)$ is known, but the same cannot be said for realistic scenarios, as no general closed-form expression exists. In this work we present an inference-based scheme for QS. We show that, for a general class of unitary families of encoding, $\mathcal{R}(\theta)$ can be fully characterized by only measuring the system response at $2n+1$ parameters. In turn, this allows us to infer the value of an unknown parameter given the measured response, as well as to determine the sensitivity of the sensing scheme, which characterizes its overall performance. We show that inference error is, with high probability, smaller than $\delta$, if one measures the system response with a number of shots that scales only as $\Omega(\log^3(n)/\delta^2)$. Furthermore, the framework presented can be broadly applied as it remains valid for arbitrary probe states and measurement schemes, and, even holds in the presence of quantum noise. We also discuss how to extend our results beyond unitary families. Finally, to showcase our method we implement it for a QS task on real quantum hardware, and in numerical simulations.

Noise-Induced Barren Plateaus in Variational Quantum Algorithms

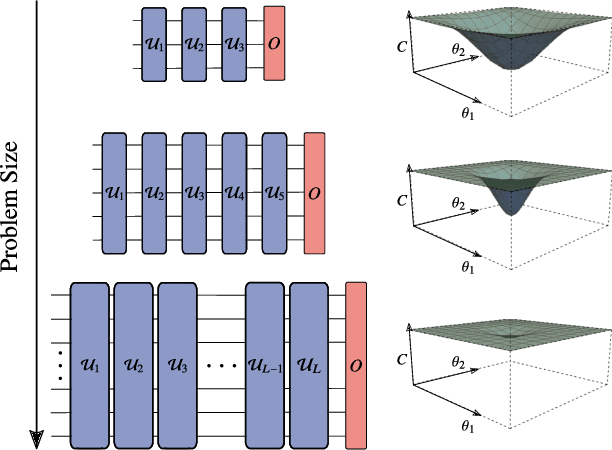
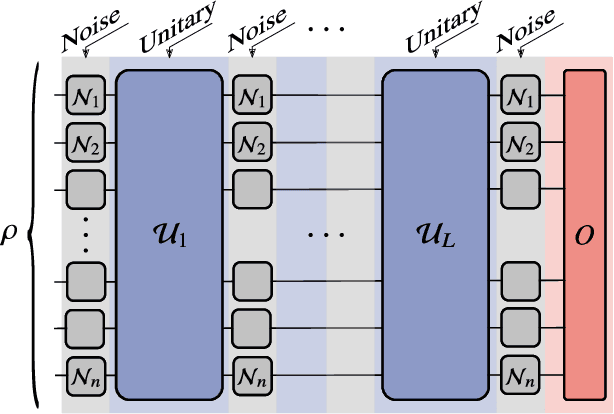
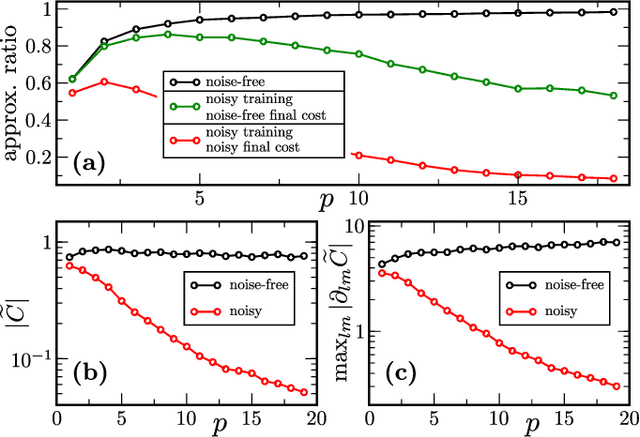
Variational Quantum Algorithms (VQAs) may be a path to quantum advantage on Noisy Intermediate-Scale Quantum (NISQ) computers. A natural question is whether the noise on NISQ devices places any fundamental limitations on the performance of VQAs. In this work, we rigorously prove a serious limitation for noisy VQAs, in that the noise causes the training landscape to have a barren plateau (i.e., vanishing gradient). Specifically, for the local Pauli noise considered, we prove that the gradient vanishes exponentially in the number of layers $L$. This implies exponential decay in the number of qubits $n$ when $L$ scales as $\operatorname{poly}(n)$, for sufficiently large coefficients in the polynomial. These noise-induced barren plateaus (NIBPs) are conceptually different from noise-free barren plateaus, which are linked to random parameter initialization. Our result is formulated for an abstract ansatz that includes as special cases the Quantum Alternating Operator Ansatz (QAOA) and the Unitary Coupled Cluster Ansatz, among others. In the case of the QAOA, we implement numerical heuristics that confirm the NIBP phenomenon for a realistic hardware noise model.

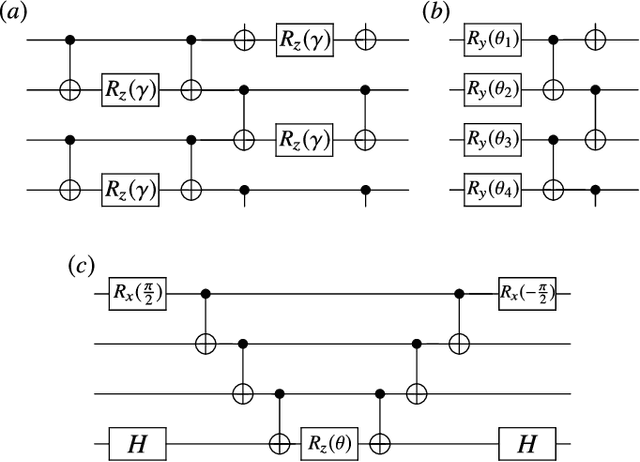
Cost-Function-Dependent Barren Plateaus in Shallow Quantum Neural Networks

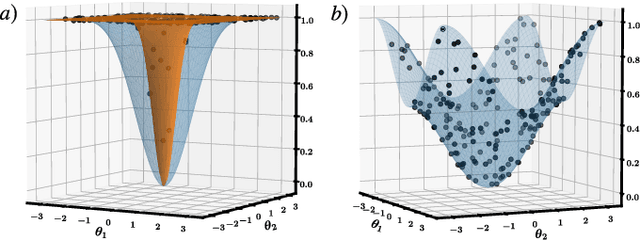
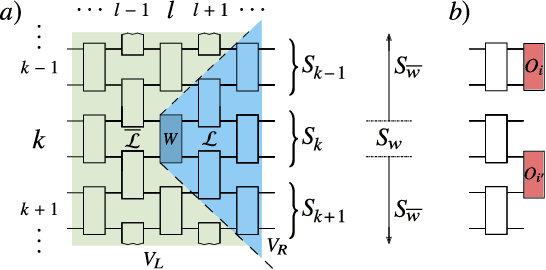
Variational quantum algorithms (VQAs) optimize the parameters $\boldsymbol{\theta}$ of a quantum neural network $V(\boldsymbol{\theta})$ to minimize a cost function $C$. While VQAs may enable practical applications of noisy quantum computers, they are nevertheless heuristic methods with unproven scaling. Here, we rigorously prove two results, assuming $V(\boldsymbol{\theta})$ is a hardware-efficient ansatz composed of blocks forming local 2-designs. Our first result states that defining $C$ in terms of global observables leads to an exponentially vanishing gradient (i.e., a barren plateau) even when $V(\boldsymbol{\theta})$ is shallow. This implies that several VQAs in the literature must revise their proposed cost functions. On the other hand, our second result states that defining $C$ with local observables leads to at worst a polynomially vanishing gradient, so long as the depth of $V(\boldsymbol{\theta})$ is $\mathcal{O}(\log n)$. Taken together, our results establish a connection between locality and trainability. Finally, we illustrate these ideas with large-scale simulations, up to 100 qubits, of a particular VQA known as quantum autoencoders.