Absence of Barren Plateaus in Quantum Convolutional Neural Networks

Quantum neural networks (QNNs) have generated excitement around the possibility of efficiently analyzing quantum data. But this excitement has been tempered by the existence of exponentially vanishing gradients, known as barren plateau landscapes, for many QNN architectures. Recently, Quantum Convolutional Neural Networks (QCNNs) have been proposed, involving a sequence of convolutional and pooling layers that reduce the number of qubits while preserving information about relevant data features. In this work we rigorously analyze the gradient scaling for the parameters in the QCNN architecture. We find that the variance of the gradient vanishes no faster than polynomially, implying that QCNNs do not exhibit barren plateaus. This provides an analytical guarantee for the trainability of randomly initialized QCNNs, which singles out QCNNs as being trainable unlike many other QNN architectures. To derive our results we introduce a novel graph-based method to analyze expectation values over Haar-distributed unitaries, which will likely be useful in other contexts. Finally, we perform numerical simulations to verify our analytical results.

Cost-Function-Dependent Barren Plateaus in Shallow Quantum Neural Networks

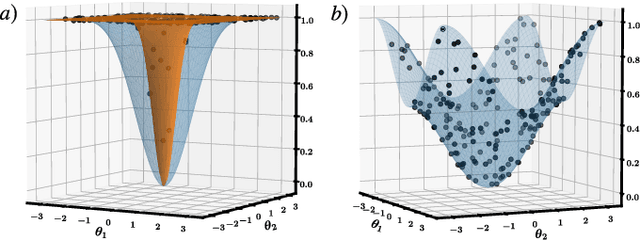
Variational quantum algorithms (VQAs) optimize the parameters $\boldsymbol{\theta}$ of a quantum neural network $V(\boldsymbol{\theta})$ to minimize a cost function $C$. While VQAs may enable practical applications of noisy quantum computers, they are nevertheless heuristic methods with unproven scaling. Here, we rigorously prove two results, assuming $V(\boldsymbol{\theta})$ is a hardware-efficient ansatz composed of blocks forming local 2-designs. Our first result states that defining $C$ in terms of global observables leads to an exponentially vanishing gradient (i.e., a barren plateau) even when $V(\boldsymbol{\theta})$ is shallow. This implies that several VQAs in the literature must revise their proposed cost functions. On the other hand, our second result states that defining $C$ with local observables leads to at worst a polynomially vanishing gradient, so long as the depth of $V(\boldsymbol{\theta})$ is $\mathcal{O}(\log n)$. Taken together, our results establish a connection between locality and trainability. Finally, we illustrate these ideas with large-scale simulations, up to 100 qubits, of a particular VQA known as quantum autoencoders.