Scalable quantum dynamics compilation via quantum machine learning

Quantum dynamics compilation is an important task for improving quantum simulation efficiency: It aims to synthesize multi-qubit target dynamics into a circuit consisting of as few elementary gates as possible. Compared to deterministic methods such as Trotterization, variational quantum compilation (VQC) methods employ variational optimization to reduce gate costs while maintaining high accuracy. In this work, we explore the potential of a VQC scheme by making use of out-of-distribution generalization results in quantum machine learning (QML): By learning the action of a given many-body dynamics on a small data set of product states, we can obtain a unitary circuit that generalizes to highly entangled states such as the Haar random states. The efficiency in training allows us to use tensor network methods to compress such time-evolved product states by exploiting their low entanglement features. Our approach exceeds state-of-the-art compilation results in both system size and accuracy in one dimension ($1$D). For the first time, we extend VQC to systems on two-dimensional (2D) strips with a quasi-1D treatment, demonstrating a significant resource advantage over standard Trotterization methods, highlighting the method's promise for advancing quantum simulation tasks on near-term quantum processors.

Variational Neural Annealing

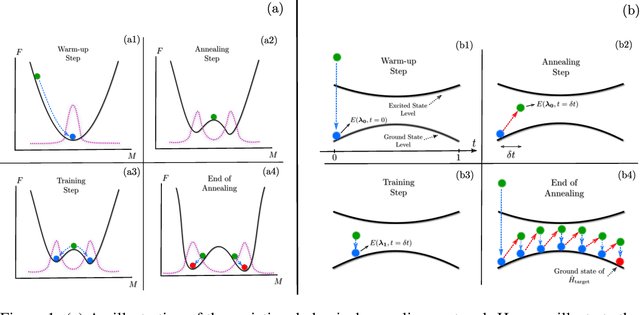
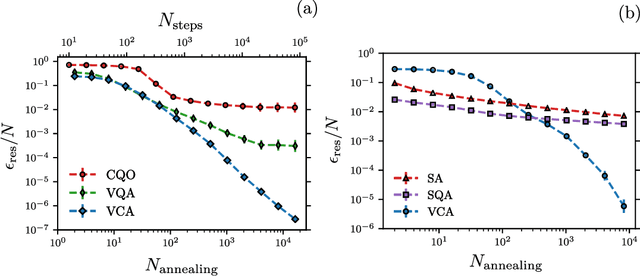
Many important challenges in science and technology can be cast as optimization problems. When viewed in a statistical physics framework, these can be tackled by simulated annealing, where a gradual cooling procedure helps search for groundstate solutions of a target Hamiltonian. While powerful, simulated annealing is known to have prohibitively slow sampling dynamics when the optimization landscape is rough or glassy. Here we show that by generalizing the target distribution with a parameterized model, an analogous annealing framework based on the variational principle can be used to search for groundstate solutions. Modern autoregressive models such as recurrent neural networks provide ideal parameterizations since they can be exactly sampled without slow dynamics even when the model encodes a rough landscape. We implement this procedure in the classical and quantum settings on several prototypical spin glass Hamiltonians, and find that it significantly outperforms traditional simulated annealing in the asymptotic limit, illustrating the potential power of this yet unexplored route to optimization.