Lattice Protein Folding with Variational Annealing

Understanding the principles of protein folding is a cornerstone of computational biology, with implications for drug design, bioengineering, and the understanding of fundamental biological processes. Lattice protein folding models offer a simplified yet powerful framework for studying the complexities of protein folding, enabling the exploration of energetically optimal folds under constrained conditions. However, finding these optimal folds is a computationally challenging combinatorial optimization problem. In this work, we introduce a novel upper-bound training scheme that employs masking to identify the lowest-energy folds in two-dimensional Hydrophobic-Polar (HP) lattice protein folding. By leveraging Dilated Recurrent Neural Networks (RNNs) integrated with an annealing process driven by temperature-like fluctuations, our method accurately predicts optimal folds for benchmark systems of up to 60 beads. Our approach also effectively masks invalid folds from being sampled without compromising the autoregressive sampling properties of RNNs. This scheme is generalizable to three spatial dimensions and can be extended to lattice protein models with larger alphabets. Our findings emphasize the potential of advanced machine learning techniques in tackling complex protein folding problems and a broader class of constrained combinatorial optimization challenges.

Variational Neural Annealing

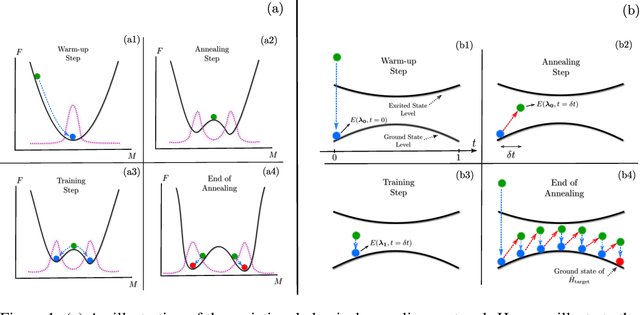
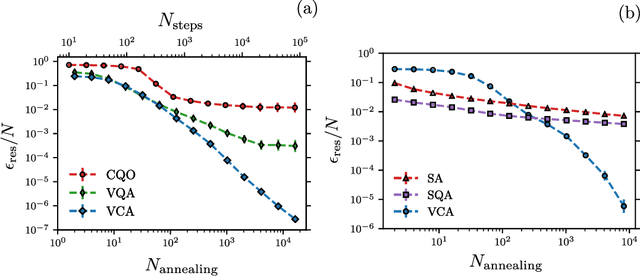
Many important challenges in science and technology can be cast as optimization problems. When viewed in a statistical physics framework, these can be tackled by simulated annealing, where a gradual cooling procedure helps search for groundstate solutions of a target Hamiltonian. While powerful, simulated annealing is known to have prohibitively slow sampling dynamics when the optimization landscape is rough or glassy. Here we show that by generalizing the target distribution with a parameterized model, an analogous annealing framework based on the variational principle can be used to search for groundstate solutions. Modern autoregressive models such as recurrent neural networks provide ideal parameterizations since they can be exactly sampled without slow dynamics even when the model encodes a rough landscape. We implement this procedure in the classical and quantum settings on several prototypical spin glass Hamiltonians, and find that it significantly outperforms traditional simulated annealing in the asymptotic limit, illustrating the potential power of this yet unexplored route to optimization.