Denis Melanson
Scalable Thermodynamic Second-order Optimization
Feb 12, 2025Abstract:Many hardware proposals have aimed to accelerate inference in AI workloads. Less attention has been paid to hardware acceleration of training, despite the enormous societal impact of rapid training of AI models. Physics-based computers, such as thermodynamic computers, offer an efficient means to solve key primitives in AI training algorithms. Optimizers that normally would be computationally out-of-reach (e.g., due to expensive matrix inversions) on digital hardware could be unlocked with physics-based hardware. In this work, we propose a scalable algorithm for employing thermodynamic computers to accelerate a popular second-order optimizer called Kronecker-factored approximate curvature (K-FAC). Our asymptotic complexity analysis predicts increasing advantage with our algorithm as $n$, the number of neurons per layer, increases. Numerical experiments show that even under significant quantization noise, the benefits of second-order optimization can be preserved. Finally, we predict substantial speedups for large-scale vision and graph problems based on realistic hardware characteristics.
Thermodynamic Bayesian Inference
Oct 02, 2024Abstract:A fully Bayesian treatment of complicated predictive models (such as deep neural networks) would enable rigorous uncertainty quantification and the automation of higher-level tasks including model selection. However, the intractability of sampling Bayesian posteriors over many parameters inhibits the use of Bayesian methods where they are most needed. Thermodynamic computing has emerged as a paradigm for accelerating operations used in machine learning, such as matrix inversion, and is based on the mapping of Langevin equations to the dynamics of noisy physical systems. Hence, it is natural to consider the implementation of Langevin sampling algorithms on thermodynamic devices. In this work we propose electronic analog devices that sample from Bayesian posteriors by realizing Langevin dynamics physically. Circuit designs are given for sampling the posterior of a Gaussian-Gaussian model and for Bayesian logistic regression, and are validated by simulations. It is shown, under reasonable assumptions, that the Bayesian posteriors for these models can be sampled in time scaling with $\ln(d)$, where $d$ is dimension. For the Gaussian-Gaussian model, the energy cost is shown to scale with $ d \ln(d)$. These results highlight the potential for fast, energy-efficient Bayesian inference using thermodynamic computing.
Thermodynamic Natural Gradient Descent
May 22, 2024Abstract:Second-order training methods have better convergence properties than gradient descent but are rarely used in practice for large-scale training due to their computational overhead. This can be viewed as a hardware limitation (imposed by digital computers). Here we show that natural gradient descent (NGD), a second-order method, can have a similar computational complexity per iteration to a first-order method, when employing appropriate hardware. We present a new hybrid digital-analog algorithm for training neural networks that is equivalent to NGD in a certain parameter regime but avoids prohibitively costly linear system solves. Our algorithm exploits the thermodynamic properties of an analog system at equilibrium, and hence requires an analog thermodynamic computer. The training occurs in a hybrid digital-analog loop, where the gradient and Fisher information matrix (or any other positive semi-definite curvature matrix) are calculated at given time intervals while the analog dynamics take place. We numerically demonstrate the superiority of this approach over state-of-the-art digital first- and second-order training methods on classification tasks and language model fine-tuning tasks.
Thermodynamic Computing System for AI Applications
Dec 08, 2023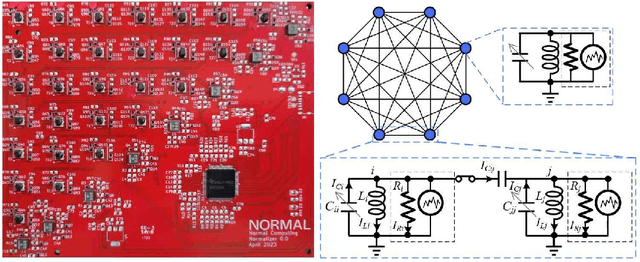
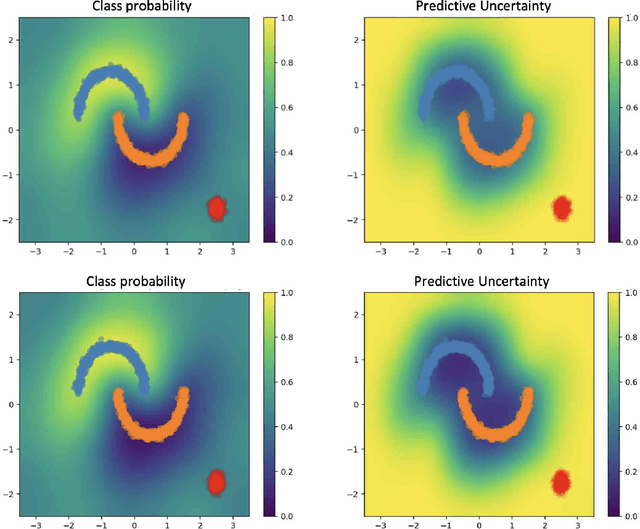
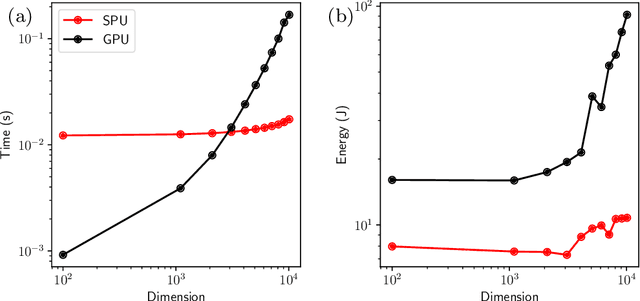
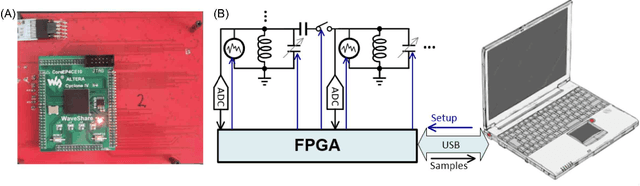
Abstract:Recent breakthroughs in artificial intelligence (AI) algorithms have highlighted the need for novel computing hardware in order to truly unlock the potential for AI. Physics-based hardware, such as thermodynamic computing, has the potential to provide a fast, low-power means to accelerate AI primitives, especially generative AI and probabilistic AI. In this work, we present the first continuous-variable thermodynamic computer, which we call the stochastic processing unit (SPU). Our SPU is composed of RLC circuits, as unit cells, on a printed circuit board, with 8 unit cells that are all-to-all coupled via switched capacitances. It can be used for either sampling or linear algebra primitives, and we demonstrate Gaussian sampling and matrix inversion on our hardware. The latter represents the first thermodynamic linear algebra experiment. We also illustrate the applicability of the SPU to uncertainty quantification for neural network classification. We envision that this hardware, when scaled up in size, will have significant impact on accelerating various probabilistic AI applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge