Adversarial robustness guarantees for random deep neural networks
Paper and Code
Apr 13, 2020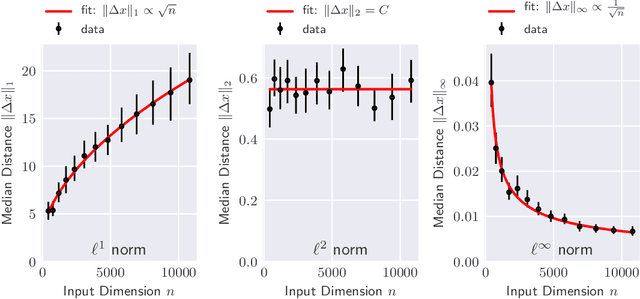
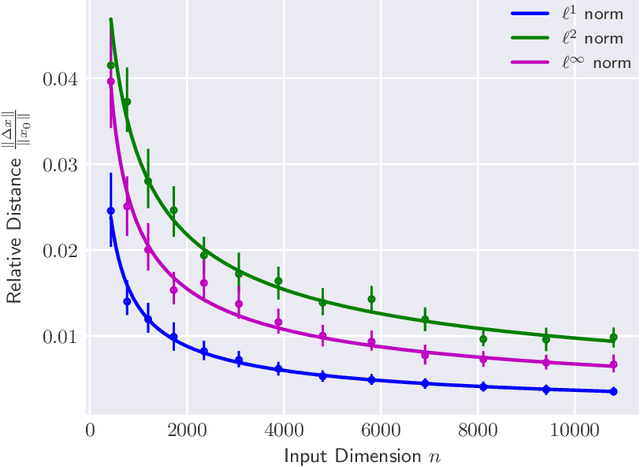
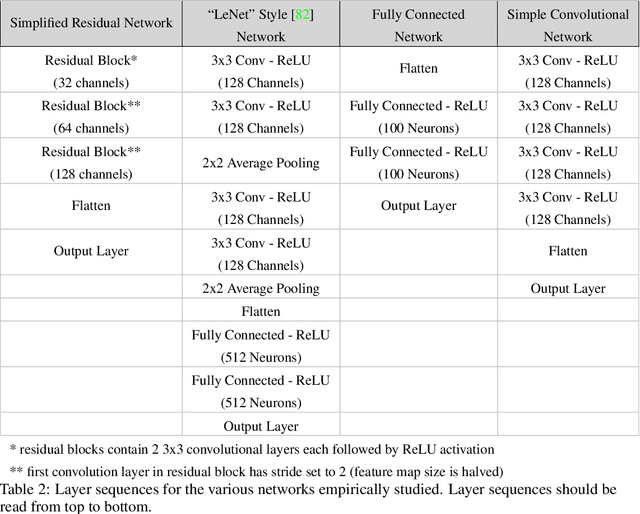
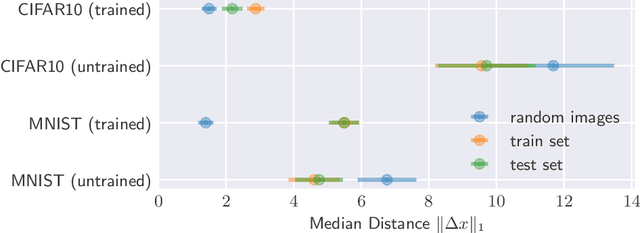
The reliability of most deep learning algorithms is fundamentally challenged by the existence of adversarial examples, which are incorrectly classified inputs that are extremely close to a correctly classified input. We study adversarial examples for deep neural networks with random weights and biases and prove that the $\ell^1$ distance of any given input from the classification boundary scales at least as $\sqrt{n}$, where $n$ is the dimension of the input. We also extend our proof to cover all the $\ell^p$ norms. Our results constitute a fundamental advance in the study of adversarial examples, and encompass a wide variety of architectures, which include any combination of convolutional or fully connected layers with skipped connections and pooling. We validate our results with experiments on both random deep neural networks and deep neural networks trained on the MNIST and CIFAR10 datasets. Given the results of our experiments on MNIST and CIFAR10, we conjecture that the proof of our adversarial robustness guarantee can be extended to trained deep neural networks. This extension will open the way to a thorough theoretical study of neural network robustness by classifying the relation between network architecture and adversarial distance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge