Neural Networks for Programming Quantum Annealers
Paper and Code
Aug 13, 2023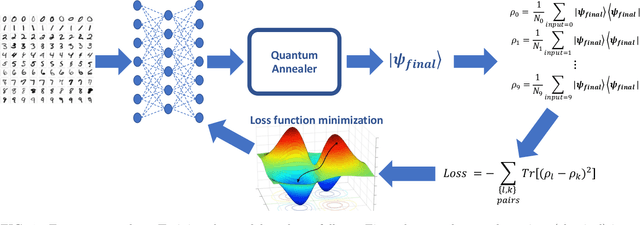
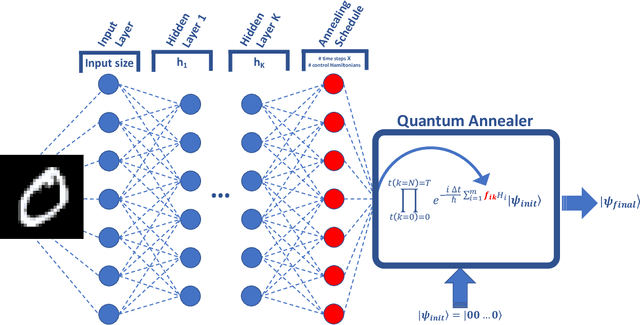
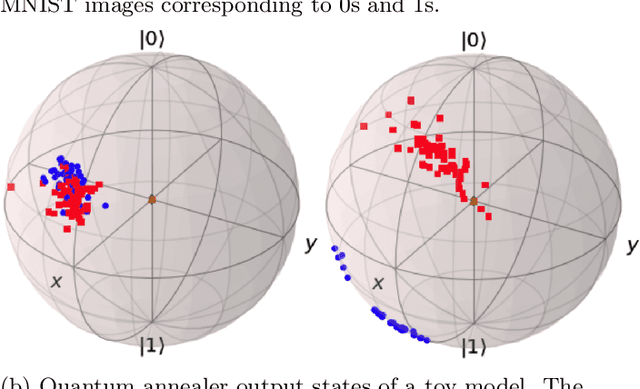
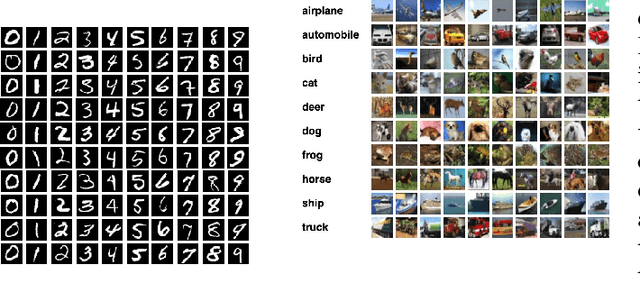
Quantum machine learning has the potential to enable advances in artificial intelligence, such as solving problems intractable on classical computers. Some fundamental ideas behind quantum machine learning are similar to kernel methods in classical machine learning. Both process information by mapping it into high-dimensional vector spaces without explicitly calculating their numerical values. We explore a setup for performing classification on labeled classical datasets, consisting of a classical neural network connected to a quantum annealer. The neural network programs the quantum annealer's controls and thereby maps the annealer's initial states into new states in the Hilbert space. The neural network's parameters are optimized to maximize the distance of states corresponding to inputs from different classes and minimize the distance between quantum states corresponding to the same class. Recent literature showed that at least some of the "learning" is due to the quantum annealer, connecting a small linear network to a quantum annealer and using it to learn small and linearly inseparable datasets. In this study, we consider a similar but not quite the same case, where a classical fully-fledged neural network is connected with a small quantum annealer. In such a setting, the fully-fledged classical neural-network already has built-in nonlinearity and learning power, and can already handle the classification problem alone, we want to see whether an additional quantum layer could boost its performance. We simulate this system to learn several common datasets, including those for image and sound recognition. We conclude that adding a small quantum annealer does not provide a significant benefit over just using a regular (nonlinear) classical neural network.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge