projUNN: efficient method for training deep networks with unitary matrices

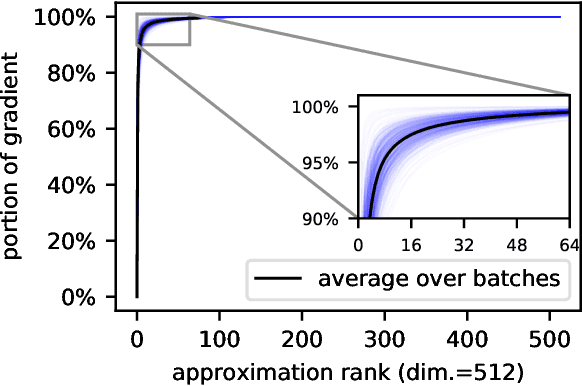
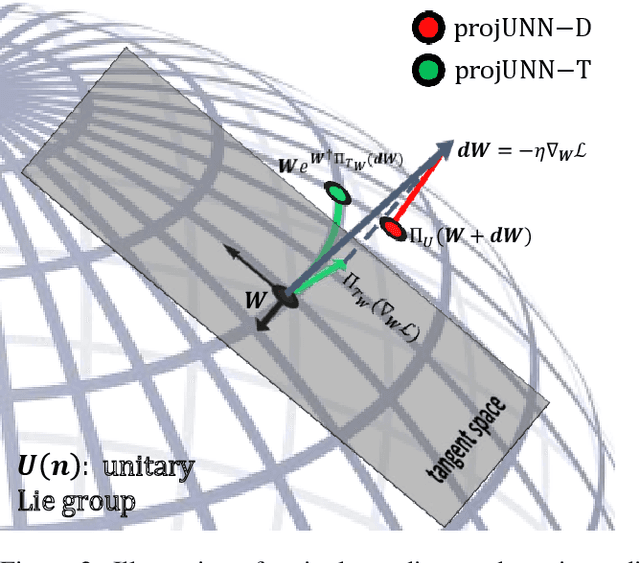
In learning with recurrent or very deep feed-forward networks, employing unitary matrices in each layer can be very effective at maintaining long-range stability. However, restricting network parameters to be unitary typically comes at the cost of expensive parameterizations or increased training runtime. We propose instead an efficient method based on rank-$k$ updates -- or their rank-$k$ approximation -- that maintains performance at a nearly optimal training runtime. We introduce two variants of this method, named Direct (projUNN-D) and Tangent (projUNN-T) projected Unitary Neural Networks, that can parameterize full $N$-dimensional unitary or orthogonal matrices with a training runtime scaling as $O(kN^2)$. Our method either projects low-rank gradients onto the closest unitary matrix (projUNN-T) or transports unitary matrices in the direction of the low-rank gradient (projUNN-D). Even in the fastest setting ($k=1$), projUNN is able to train a model's unitary parameters to reach comparable performances against baseline implementations. By integrating our projUNN algorithm into both recurrent and convolutional neural networks, our models can closely match or exceed benchmarked results from state-of-the-art algorithms.