Deterministic fast and stable phase retrieval in multiple dimensions

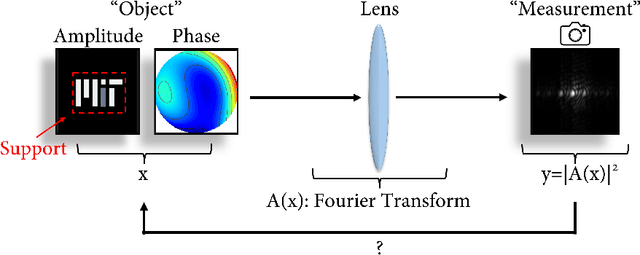
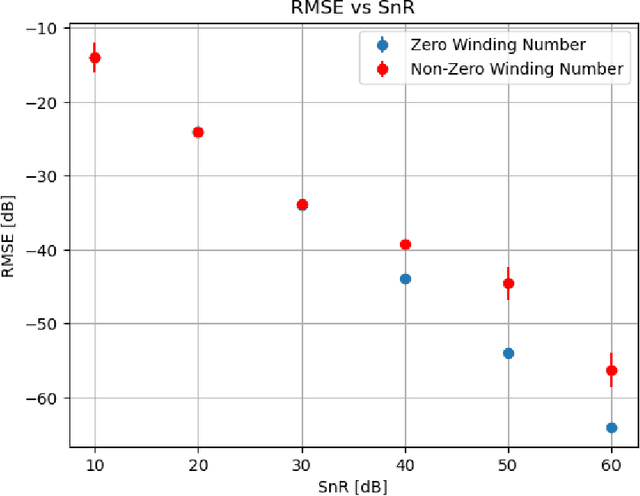
We present the first phase retrieval algorithm guaranteed to solve the multidimensional phase retrieval problem in polynomial arithmetic complexity without prior information. The method successfully terminates in O(N log(N)) operations for Fourier measurements with cardinality N. The algorithm is guaranteed to succeed for a large class of objects, which we term "Schwarz objects". We further present an easy-to-calculate and well-conditioned diagonal operator that transforms any feasible phase-retrieval instance into one that is solved by our method. We derive our method by combining techniques from classical complex analysis, algebraic topology, and modern numerical analysis. Concretely, we pose the phase retrieval problem as a multiplicative Cousin problem, construct an approximate solution using a modified integral used for the Schwarz problem, and refine the approximate solution to an exact solution via standard optimization methods. We present numerical experimentation demonstrating our algorithm's performance and its superiority to existing method. Finally, we demonstrate that our method is robust against Gaussian noise.

Designing Nonlinear Photonic Crystals for High-Dimensional Quantum State Engineering

We propose a novel, physically-constrained and differentiable approach for the generation of D-dimensional qudit states via spontaneous parametric down-conversion (SPDC) in quantum optics. We circumvent any limitations imposed by the inherently stochastic nature of the physical process and incorporate a set of stochastic dynamical equations governing its evolution under the SPDC Hamiltonian. We demonstrate the effectiveness of our model through the design of structured nonlinear photonic crystals (NLPCs) and shaped pump beams; and show, theoretically and experimentally, how to generate maximally entangled states in the spatial degree of freedom. The learning of NLPC structures offers a promising new avenue for shaping and controlling arbitrary quantum states and enables all-optical coherent control of the generated states. We believe that this approach can readily be extended from bulky crystals to thin Metasurfaces and potentially applied to other quantum systems sharing a similar Hamiltonian structures, such as superfluids and superconductors.

Single-Shot Optical Neural Network

As deep neural networks (DNNs) grow to solve increasingly complex problems, they are becoming limited by the latency and power consumption of existing digital processors. 'Weight-stationary' analog optical and electronic hardware has been proposed to reduce the compute resources required by DNNs by eliminating expensive weight updates; however, with scalability limited to an input vector length $K$ of hundreds of elements. Here, we present a scalable, single-shot-per-layer weight-stationary optical processor that leverages the advantages of free-space optics for passive optical copying and large-scale distribution of an input vector and integrated optoelectronics for static, reconfigurable weighting and the nonlinearity. We propose an optimized near-term CMOS-compatible system with $K = 1,000$ and beyond, and we calculate its theoretical total latency ($\sim$10 ns), energy consumption ($\sim$10 fJ/MAC) and throughput ($\sim$petaMAC/s) per layer. We also experimentally test DNN classification accuracy with single-shot analog optical encoding, copying and weighting of the MNIST handwritten digit dataset in a proof-of-concept system, achieving 94.7% (similar to the ground truth accuracy of 96.3%) without retraining on the hardware or data preprocessing. Lastly, we determine the upper bound on throughput of our system ($\sim$0.9 exaMAC/s), set by the maximum optical bandwidth before significant loss of accuracy. This joint use of wide spectral and spatial bandwidths enables highly efficient computing for next-generation DNNs.

SPDCinv: Inverse Quantum-Optical Design of High-Dimensional Qudits

Spontaneous parametric down-conversion in quantum optics is an invaluable resource for the realization of high-dimensional qudits with spatial modes of light. One of the main open challenges is how to directly generate a desirable qudit state in the SPDC process. This problem can be addressed through advanced computational learning methods; however, due to difficulties in modeling the SPDC process by a fully differentiable algorithm that takes into account all interaction effects, progress has been limited. Here, we overcome these limitations and introduce a physically-constrained and differentiable model, validated against experimental results for shaped pump beams and structured crystals, capable of learning every interaction parameter in the process. We avoid any restrictions induced by the stochastic nature of our physical model and integrate the dynamic equations governing the evolution under the SPDC Hamiltonian. We solve the inverse problem of designing a nonlinear quantum optical system that achieves the desired quantum state of down-converted photon pairs. The desired states are defined using either the second-order correlations between different spatial modes or by specifying the required density matrix. By learning nonlinear volume holograms as well as different pump shapes, we successfully show how to generate maximally entangled states. Furthermore, we simulate all-optical coherent control over the generated quantum state by actively changing the profile of the pump beam. Our work can be useful for applications such as novel designs of high-dimensional quantum key distribution and quantum information processing protocols. In addition, our method can be readily applied for controlling other degrees of freedom of light in the SPDC process, such as the spectral and temporal properties, and may even be used in condensed-matter systems having a similar interaction Hamiltonian.

Inverse Design of Quantum Holograms in Three-Dimensional Nonlinear Photonic Crystals

We introduce a systematic approach for designing 3D nonlinear photonic crystals and pump beams for generating desired quantum correlations between structured photon-pairs. Our model is fully differentiable, allowing accurate and efficient learning and discovery of novel designs.