Quantum-secure multiparty deep learning

Secure multiparty computation enables the joint evaluation of multivariate functions across distributed users while ensuring the privacy of their local inputs. This field has become increasingly urgent due to the exploding demand for computationally intensive deep learning inference. These computations are typically offloaded to cloud computing servers, leading to vulnerabilities that can compromise the security of the clients' data. To solve this problem, we introduce a linear algebra engine that leverages the quantum nature of light for information-theoretically secure multiparty computation using only conventional telecommunication components. We apply this linear algebra engine to deep learning and derive rigorous upper bounds on the information leakage of both the deep neural network weights and the client's data via the Holevo and the Cram\'er-Rao bounds, respectively. Applied to the MNIST classification task, we obtain test accuracies exceeding $96\%$ while leaking less than $0.1$ bits per weight symbol and $0.01$ bits per data symbol. This weight leakage is an order of magnitude below the minimum bit precision required for accurate deep learning using state-of-the-art quantization techniques. Our work lays the foundation for practical quantum-secure computation and unlocks secure cloud deep learning as a field.

Frequency-Encoded Deep Learning with Speed-of-Light Dominated Latency

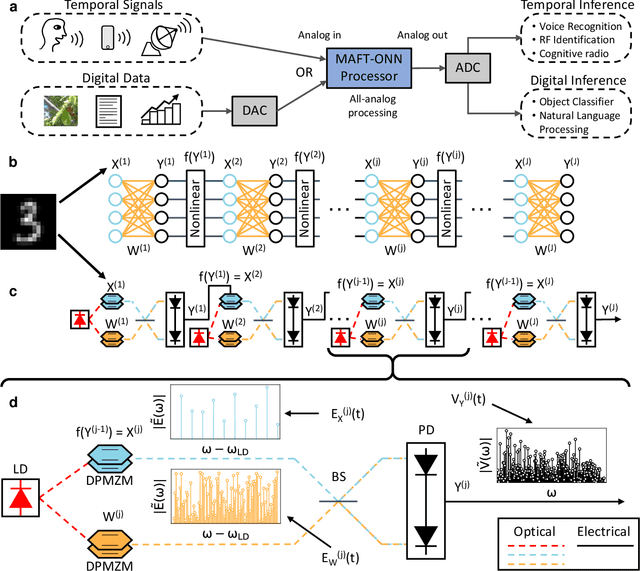
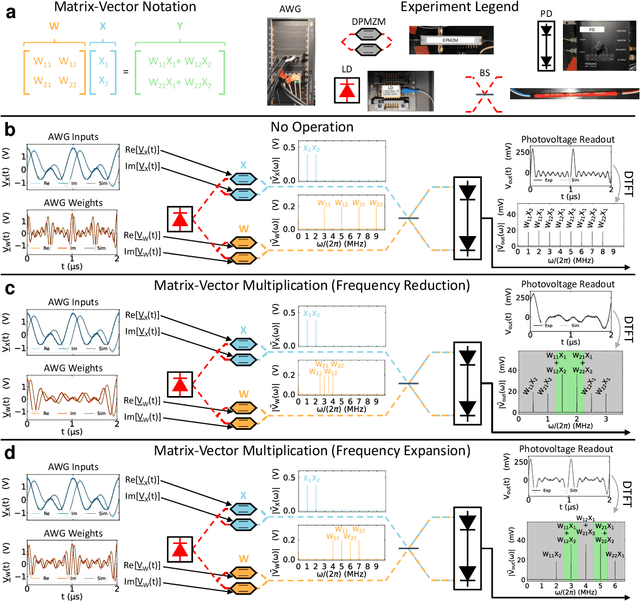
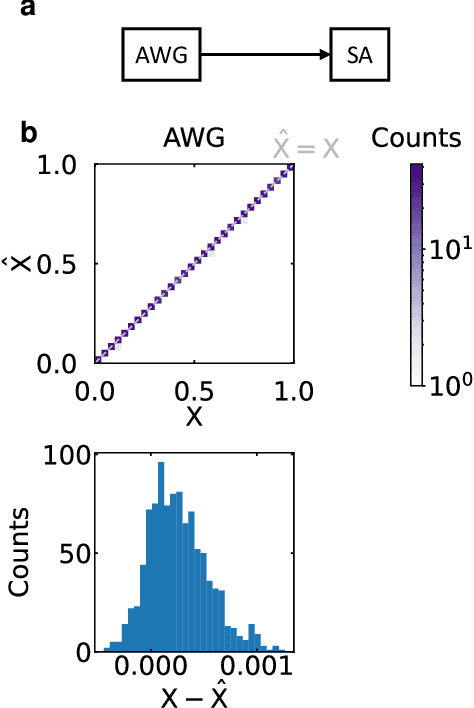
The ability of deep neural networks to perform complex tasks more accurately than manually-crafted solutions has created a substantial demand for more complex models processing larger amounts of data. However, the traditional computing architecture has reached a bottleneck in processing performance due to data movement from memory to computing. Considerable efforts have been made towards custom hardware acceleration, among which are optical neural networks (ONNs). These excel at energy efficient linear operations but struggle with scalability and the integration of linear and nonlinear functions. Here, we introduce our multiplicative analog frequency transform optical neural network (MAFT-ONN) that encodes the data in the frequency domain to compute matrix-vector products in a single-shot using a single photoelectric multiplication, and then implements the nonlinear activation for all neurons using a single electro-optic modulator. We experimentally demonstrate a 3-layer DNN with our architecture using a simple hardware setup assembled with commercial components. Additionally, this is the first DNN hardware accelerator suitable for analog inference of temporal waveforms like voice or radio signals, achieving bandwidth-limited throughput and speed-of-light limited latency. Our results demonstrate a highly scalable ONN with a straightforward path to surpassing the current computing bottleneck, in addition to enabling new possibilities for high-performance analog deep learning of temporal waveforms.

Single-Shot Optical Neural Network

As deep neural networks (DNNs) grow to solve increasingly complex problems, they are becoming limited by the latency and power consumption of existing digital processors. 'Weight-stationary' analog optical and electronic hardware has been proposed to reduce the compute resources required by DNNs by eliminating expensive weight updates; however, with scalability limited to an input vector length $K$ of hundreds of elements. Here, we present a scalable, single-shot-per-layer weight-stationary optical processor that leverages the advantages of free-space optics for passive optical copying and large-scale distribution of an input vector and integrated optoelectronics for static, reconfigurable weighting and the nonlinearity. We propose an optimized near-term CMOS-compatible system with $K = 1,000$ and beyond, and we calculate its theoretical total latency ($\sim$10 ns), energy consumption ($\sim$10 fJ/MAC) and throughput ($\sim$petaMAC/s) per layer. We also experimentally test DNN classification accuracy with single-shot analog optical encoding, copying and weighting of the MNIST handwritten digit dataset in a proof-of-concept system, achieving 94.7% (similar to the ground truth accuracy of 96.3%) without retraining on the hardware or data preprocessing. Lastly, we determine the upper bound on throughput of our system ($\sim$0.9 exaMAC/s), set by the maximum optical bandwidth before significant loss of accuracy. This joint use of wide spectral and spatial bandwidths enables highly efficient computing for next-generation DNNs.