Molecular Diffusion Models with Virtual Receptors

Machine learning approaches to Structure-Based Drug Design (SBDD) have proven quite fertile over the last few years. In particular, diffusion-based approaches to SBDD have shown great promise. We present a technique which expands on this diffusion approach in two crucial ways. First, we address the size disparity between the drug molecule and the target/receptor, which makes learning more challenging and inference slower. We do so through the notion of a Virtual Receptor, which is a compressed version of the receptor; it is learned so as to preserve key aspects of the structural information of the original receptor, while respecting the relevant group equivariance. Second, we incorporate a protein language embedding used originally in the context of protein folding. We experimentally demonstrate the contributions of both the virtual receptors and the protein embeddings: in practice, they lead to both better performance, as well as significantly faster computations.

A Theoretical Framework for an Efficient Normalizing Flow-Based Solution to the Schrodinger Equation

A central problem in quantum mechanics involves solving the Electronic Schrodinger Equation for a molecule or material. The Variational Monte Carlo approach to this problem approximates a particular variational objective via sampling, and then optimizes this approximated objective over a chosen parameterized family of wavefunctions, known as the ansatz. Recently neural networks have been used as the ansatz, with accompanying success. However, sampling from such wavefunctions has required the use of a Markov Chain Monte Carlo approach, which is inherently inefficient. In this work, we propose a solution to this problem via an ansatz which is cheap to sample from, yet satisfies the requisite quantum mechanical properties. We prove that a normalizing flow using the following two essential ingredients satisfies our requirements: (a) a base distribution which is constructed from Determinantal Point Processes; (b) flow layers which are equivariant to a particular subgroup of the permutation group. We then show how to construct both continuous and discrete normalizing flows which satisfy the requisite equivariance. We further demonstrate the manner in which the non-smooth nature ("cusps") of the wavefunction may be captured, and how the framework may be generalized to provide induction across multiple molecules. The resulting theoretical framework entails an efficient approach to solving the Electronic Schrodinger Equation.

Overcoming Order in Autoregressive Graph Generation

Graph generation is a fundamental problem in various domains, including chemistry and social networks. Recent work has shown that molecular graph generation using recurrent neural networks (RNNs) is advantageous compared to traditional generative approaches which require converting continuous latent representations into graphs. One issue which arises when treating graph generation as sequential generation is the arbitrary order of the sequence which results from a particular choice of graph flattening method. In this work we propose using RNNs, taking into account the non-sequential nature of graphs by adding an Orderless Regularization (OLR) term that encourages the hidden state of the recurrent model to be invariant to different valid orderings present under the training distribution. We demonstrate that sequential graph generation models benefit from our proposed regularization scheme, especially when data is scarce. Our findings contribute to the growing body of research on graph generation and provide a valuable tool for various applications requiring the synthesis of realistic and diverse graph structures.

Semi-Equivariant Conditional Normalizing Flows

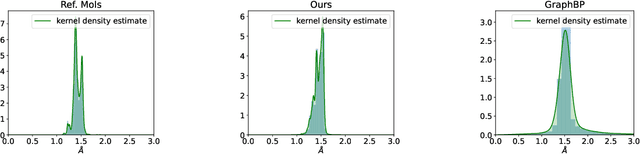
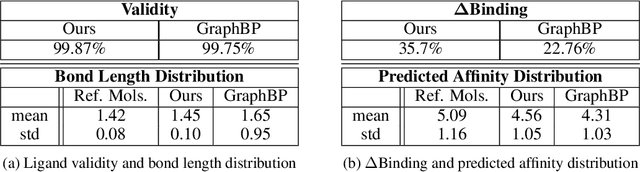
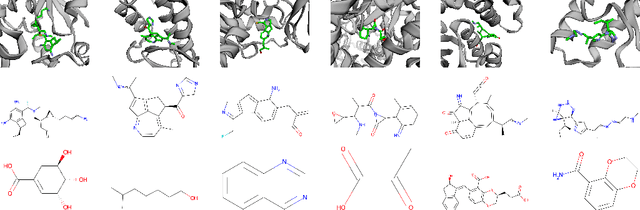
We study the problem of learning conditional distributions of the form $p(G | \hat G)$, where $G$ and $\hat G$ are two 3D graphs, using continuous normalizing flows. We derive a semi-equivariance condition on the flow which ensures that conditional invariance to rigid motions holds. We demonstrate the effectiveness of the technique in the molecular setting of receptor-aware ligand generation.

Designing Nonlinear Photonic Crystals for High-Dimensional Quantum State Engineering

We propose a novel, physically-constrained and differentiable approach for the generation of D-dimensional qudit states via spontaneous parametric down-conversion (SPDC) in quantum optics. We circumvent any limitations imposed by the inherently stochastic nature of the physical process and incorporate a set of stochastic dynamical equations governing its evolution under the SPDC Hamiltonian. We demonstrate the effectiveness of our model through the design of structured nonlinear photonic crystals (NLPCs) and shaped pump beams; and show, theoretically and experimentally, how to generate maximally entangled states in the spatial degree of freedom. The learning of NLPC structures offers a promising new avenue for shaping and controlling arbitrary quantum states and enables all-optical coherent control of the generated states. We believe that this approach can readily be extended from bulky crystals to thin Metasurfaces and potentially applied to other quantum systems sharing a similar Hamiltonian structures, such as superfluids and superconductors.

Semi-Equivariant Continuous Normalizing Flows for Target-Aware Molecule Generation

We propose an algorithm for learning a conditional generative model of a molecule given a target. Specifically, given a receptor molecule that one wishes to bind to, the conditional model generates candidate ligand molecules that may bind to it. The distribution should be invariant to rigid body transformations that act $\textit{jointly}$ on the ligand and the receptor; it should also be invariant to permutations of either the ligand or receptor atoms. Our learning algorithm is based on a continuous normalizing flow. We establish semi-equivariance conditions on the flow which guarantee the aforementioned invariance conditions on the conditional distribution. We propose a graph neural network architecture which implements this flow, and which is designed to learn effectively despite the vast differences in size between the ligand and receptor. We evaluate our method on the CrossDocked2020 dataset, attaining a significant improvement in binding affinity over competing methods.

SPDCinv: Inverse Quantum-Optical Design of High-Dimensional Qudits

Spontaneous parametric down-conversion in quantum optics is an invaluable resource for the realization of high-dimensional qudits with spatial modes of light. One of the main open challenges is how to directly generate a desirable qudit state in the SPDC process. This problem can be addressed through advanced computational learning methods; however, due to difficulties in modeling the SPDC process by a fully differentiable algorithm that takes into account all interaction effects, progress has been limited. Here, we overcome these limitations and introduce a physically-constrained and differentiable model, validated against experimental results for shaped pump beams and structured crystals, capable of learning every interaction parameter in the process. We avoid any restrictions induced by the stochastic nature of our physical model and integrate the dynamic equations governing the evolution under the SPDC Hamiltonian. We solve the inverse problem of designing a nonlinear quantum optical system that achieves the desired quantum state of down-converted photon pairs. The desired states are defined using either the second-order correlations between different spatial modes or by specifying the required density matrix. By learning nonlinear volume holograms as well as different pump shapes, we successfully show how to generate maximally entangled states. Furthermore, we simulate all-optical coherent control over the generated quantum state by actively changing the profile of the pump beam. Our work can be useful for applications such as novel designs of high-dimensional quantum key distribution and quantum information processing protocols. In addition, our method can be readily applied for controlling other degrees of freedom of light in the SPDC process, such as the spectral and temporal properties, and may even be used in condensed-matter systems having a similar interaction Hamiltonian.

Inverse Design of Quantum Holograms in Three-Dimensional Nonlinear Photonic Crystals

We introduce a systematic approach for designing 3D nonlinear photonic crystals and pump beams for generating desired quantum correlations between structured photon-pairs. Our model is fully differentiable, allowing accurate and efficient learning and discovery of novel designs.

Localization with Limited Annotation for Chest X-rays

Localization of an object within an image is a common task in medical imaging. Learning to localize or detect objects typically requires the collection of data which has been labelled with bounding boxes or similar annotations, which can be very time consuming and expensive. A technique which could perform such learning with much less annotation would, therefore, be quite valuable. We present such a technique for localization with limited annotation, in which the number of images with bounding boxes can be a small fraction of the total dataset (e.g. less than 1%); all other images only possess a whole image label and no bounding box. We propose a novel loss function for tackling this problem; the loss is a continuous relaxation of a well-defined discrete formulation of weakly supervised learning and is numerically well-posed. Furthermore, we propose a new architecture which accounts for both patch dependence and shift-invariance, through the inclusion of CRF layers and anti-aliasing filters, respectively. We apply our technique to the localization of thoracic diseases in chest X-ray images and demonstrate state-of-the-art localization performance on the ChestX-ray14 dataset.