SP2RINT: Spatially-Decoupled Physics-Inspired Progressive Inverse Optimization for Scalable, PDE-Constrained Meta-Optical Neural Network Training

DONNs harness the physics of light propagation for efficient analog computation, with applications in AI and signal processing. Advances in nanophotonic fabrication and metasurface-based wavefront engineering have opened new pathways to realize high-capacity DONNs across various spectral regimes. Training such DONN systems to determine the metasurface structures remains challenging. Heuristic methods are fast but oversimplify metasurfaces modulation, often resulting in physically unrealizable designs and significant performance degradation. Simulation-in-the-loop training methods directly optimize a physically implementable metasurface using adjoint methods during end-to-end DONN training, but are inherently computationally prohibitive and unscalable.To address these limitations, we propose SP2RINT, a spatially decoupled, progressive training framework that formulates DONN training as a PDE-constrained learning problem. Metasurface responses are first relaxed into freely trainable transfer matrices with a banded structure. We then progressively enforce physical constraints by alternating between transfer matrix training and adjoint-based inverse design, avoiding per-iteration PDE solves while ensuring final physical realizability. To further reduce runtime, we introduce a physics-inspired, spatially decoupled inverse design strategy based on the natural locality of field interactions. This approach partitions the metasurface into independently solvable patches, enabling scalable and parallel inverse design with system-level calibration. Evaluated across diverse DONN training tasks, SP2RINT achieves digital-comparable accuracy while being 1825 times faster than simulation-in-the-loop approaches. By bridging the gap between abstract DONN models and implementable photonic hardware, SP2RINT enables scalable, high-performance training of physically realizable meta-optical neural systems.

RL Tango: Reinforcing Generator and Verifier Together for Language Reasoning

Reinforcement learning (RL) has recently emerged as a compelling approach for enhancing the reasoning capabilities of large language models (LLMs), where an LLM generator serves as a policy guided by a verifier (reward model). However, current RL post-training methods for LLMs typically use verifiers that are fixed (rule-based or frozen pretrained) or trained discriminatively via supervised fine-tuning (SFT). Such designs are susceptible to reward hacking and generalize poorly beyond their training distributions. To overcome these limitations, we propose Tango, a novel framework that uses RL to concurrently train both an LLM generator and a verifier in an interleaved manner. A central innovation of Tango is its generative, process-level LLM verifier, which is trained via RL and co-evolves with the generator. Importantly, the verifier is trained solely based on outcome-level verification correctness rewards without requiring explicit process-level annotations. This generative RL-trained verifier exhibits improved robustness and superior generalization compared to deterministic or SFT-trained verifiers, fostering effective mutual reinforcement with the generator. Extensive experiments demonstrate that both components of Tango achieve state-of-the-art results among 7B/8B-scale models: the generator attains best-in-class performance across five competition-level math benchmarks and four challenging out-of-domain reasoning tasks, while the verifier leads on the ProcessBench dataset. Remarkably, both components exhibit particularly substantial improvements on the most difficult mathematical reasoning problems. Code is at: https://github.com/kaiwenzha/rl-tango.

Simple Feedfoward Neural Networks are Almost All You Need for Time Series Forecasting

Time series data are everywhere -- from finance to healthcare -- and each domain brings its own unique complexities and structures. While advanced models like Transformers and graph neural networks (GNNs) have gained popularity in time series forecasting, largely due to their success in tasks like language modeling, their added complexity is not always necessary. In our work, we show that simple feedforward neural networks (SFNNs) can achieve performance on par with, or even exceeding, these state-of-the-art models, while being simpler, smaller, faster, and more robust. Our analysis indicates that, in many cases, univariate SFNNs are sufficient, implying that modeling interactions between multiple series may offer only marginal benefits. Even when inter-series relationships are strong, a basic multivariate SFNN still delivers competitive results. We also examine some key design choices and offer guidelines on making informed decisions. Additionally, we critique existing benchmarking practices and propose an improved evaluation protocol. Although SFNNs may not be optimal for every situation (hence the ``almost'' in our title) they serve as a strong baseline that future time series forecasting methods should always be compared against.

MAPS: Multi-Fidelity AI-Augmented Photonic Simulation and Inverse Design Infrastructure

Inverse design has emerged as a transformative approach for photonic device optimization, enabling the exploration of high-dimensional, non-intuitive design spaces to create ultra-compact devices and advance photonic integrated circuits (PICs) in computing and interconnects. However, practical challenges, such as suboptimal device performance, limited manufacturability, high sensitivity to variations, computational inefficiency, and lack of interpretability, have hindered its adoption in commercial hardware. Recent advancements in AI-assisted photonic simulation and design offer transformative potential, accelerating simulations and design generation by orders of magnitude over traditional numerical methods. Despite these breakthroughs, the lack of an open-source, standardized infrastructure and evaluation benchmark limits accessibility and cross-disciplinary collaboration. To address this, we introduce MAPS, a multi-fidelity AI-augmented photonic simulation and inverse design infrastructure designed to bridge this gap. MAPS features three synergistic components: (1) MAPS-Data: A dataset acquisition framework for generating multi-fidelity, richly labeled devices, providing high-quality data for AI-for-optics research. (2) MAPS-Train: A flexible AI-for-photonics training framework offering a hierarchical data loading pipeline, customizable model construction, support for data- and physics-driven losses, and comprehensive evaluations. (3) MAPS-InvDes: An advanced adjoint inverse design toolkit that abstracts complex physics but exposes flexible optimization steps, integrates pre-trained AI models, and incorporates fabrication variation models. This infrastructure MAPS provides a unified, open-source platform for developing, benchmarking, and advancing AI-assisted photonic design workflows, accelerating innovation in photonic hardware optimization and scientific machine learning.

REG: Rectified Gradient Guidance for Conditional Diffusion Models

Guidance techniques are simple yet effective for improving conditional generation in diffusion models. Albeit their empirical success, the practical implementation of guidance diverges significantly from its theoretical motivation. In this paper, we reconcile this discrepancy by replacing the scaled marginal distribution target, which we prove theoretically invalid, with a valid scaled joint distribution objective. Additionally, we show that the established guidance implementations are approximations to the intractable optimal solution under no future foresight constraint. Building on these theoretical insights, we propose rectified gradient guidance (REG), a versatile enhancement designed to boost the performance of existing guidance methods. Experiments on 1D and 2D demonstrate that REG provides a better approximation to the optimal solution than prior guidance techniques, validating the proposed theoretical framework. Extensive experiments on class-conditional ImageNet and text-to-image generation tasks show that incorporating REG consistently improves FID and Inception/CLIP scores across various settings compared to its absence.

PIC2O-Sim: A Physics-Inspired Causality-Aware Dynamic Convolutional Neural Operator for Ultra-Fast Photonic Device FDTD Simulation

The finite-difference time-domain (FDTD) method, which is important in photonic hardware design flow, is widely adopted to solve time-domain Maxwell equations. However, FDTD is known for its prohibitive runtime cost, taking minutes to hours to simulate a single device. Recently, AI has been applied to realize orders-of-magnitude speedup in partial differential equation (PDE) solving. However, AI-based FDTD solvers for photonic devices have not been clearly formulated. Directly applying off-the-shelf models to predict the optical field dynamics shows unsatisfying fidelity and efficiency since the model primitives are agnostic to the unique physical properties of Maxwell equations and lack algorithmic customization. In this work, we thoroughly investigate the synergy between neural operator designs and the physical property of Maxwell equations and introduce a physics-inspired AI-based FDTD prediction framework PIC2O-Sim which features a causality-aware dynamic convolutional neural operator as its backbone model that honors the space-time causality constraints via careful receptive field configuration and explicitly captures the permittivity-dependent light propagation behavior via an efficient dynamic convolution operator. Meanwhile, we explore the trade-offs among prediction scalability, fidelity, and efficiency via a multi-stage partitioned time-bundling technique in autoregressive prediction. Multiple key techniques have been introduced to mitigate iterative error accumulation while maintaining efficiency advantages during autoregressive field prediction. Extensive evaluations on three challenging photonic device simulation tasks have shown the superiority of our PIC2O-Sim method, showing 51.2% lower roll-out prediction error, 23.5 times fewer parameters than state-of-the-art neural operators, providing 300-600x higher simulation speed than an open-source FDTD numerical solver.

Rare Event Probability Learning by Normalizing Flows

A rare event is defined by a low probability of occurrence. Accurate estimation of such small probabilities is of utmost importance across diverse domains. Conventional Monte Carlo methods are inefficient, demanding an exorbitant number of samples to achieve reliable estimates. Inspired by the exact sampling capabilities of normalizing flows, we revisit this challenge and propose normalizing flow assisted importance sampling, termed NOFIS. NOFIS first learns a sequence of proposal distributions associated with predefined nested subset events by minimizing KL divergence losses. Next, it estimates the rare event probability by utilizing importance sampling in conjunction with the last proposal. The efficacy of our NOFIS method is substantiated through comprehensive qualitative visualizations, affirming the optimality of the learned proposal distribution, as well as a series of quantitative experiments encompassing $10$ distinct test cases, which highlight NOFIS's superiority over baseline approaches.

KirchhoffNet: A Circuit Bridging Message Passing and Continuous-Depth Models

In this paper, we exploit a fundamental principle of analog electronic circuitry, Kirchhoff's current law, to introduce a unique class of neural network models that we refer to as KirchhoffNet. KirchhoffNet establishes close connections with message passing neural networks and continuous-depth networks. We demonstrate that even in the absence of any traditional layers (such as convolution, pooling, or linear layers), KirchhoffNet attains 98.86% test accuracy on the MNIST dataset, comparable with state of the art (SOTA) results. What makes KirchhoffNet more intriguing is its potential in the realm of hardware. Contemporary deep neural networks are conventionally deployed on GPUs. In contrast, KirchhoffNet can be physically realized by an analog electronic circuit. Moreover, we justify that irrespective of the number of parameters within a KirchhoffNet, its forward calculation can always be completed within 1/f seconds, with f representing the hardware's clock frequency. This characteristic introduces a promising technology for implementing ultra-large-scale neural networks.

Nominality Score Conditioned Time Series Anomaly Detection by Point/Sequential Reconstruction

Time series anomaly detection is challenging due to the complexity and variety of patterns that can occur. One major difficulty arises from modeling time-dependent relationships to find contextual anomalies while maintaining detection accuracy for point anomalies. In this paper, we propose a framework for unsupervised time series anomaly detection that utilizes point-based and sequence-based reconstruction models. The point-based model attempts to quantify point anomalies, and the sequence-based model attempts to quantify both point and contextual anomalies. Under the formulation that the observed time point is a two-stage deviated value from a nominal time point, we introduce a nominality score calculated from the ratio of a combined value of the reconstruction errors. We derive an induced anomaly score by further integrating the nominality score and anomaly score, then theoretically prove the superiority of the induced anomaly score over the original anomaly score under certain conditions. Extensive studies conducted on several public datasets show that the proposed framework outperforms most state-of-the-art baselines for time series anomaly detection.

NeurOLight: A Physics-Agnostic Neural Operator Enabling Parametric Photonic Device Simulation

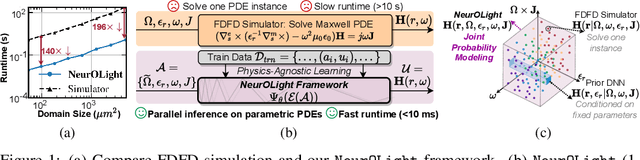
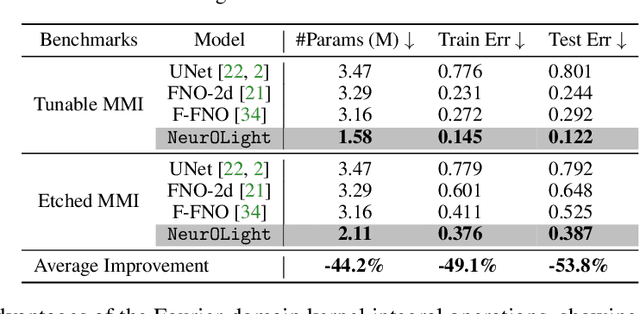
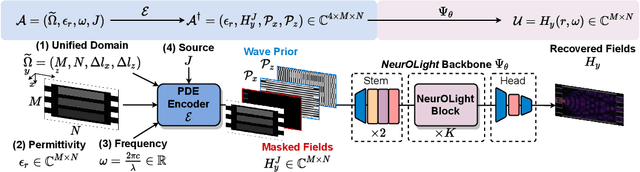
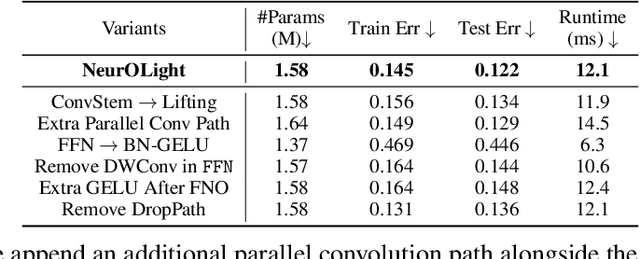
Optical computing is an emerging technology for next-generation efficient artificial intelligence (AI) due to its ultra-high speed and efficiency. Electromagnetic field simulation is critical to the design, optimization, and validation of photonic devices and circuits. However, costly numerical simulation significantly hinders the scalability and turn-around time in the photonic circuit design loop. Recently, physics-informed neural networks have been proposed to predict the optical field solution of a single instance of a partial differential equation (PDE) with predefined parameters. Their complicated PDE formulation and lack of efficient parametrization mechanisms limit their flexibility and generalization in practical simulation scenarios. In this work, for the first time, a physics-agnostic neural operator-based framework, dubbed NeurOLight, is proposed to learn a family of frequency-domain Maxwell PDEs for ultra-fast parametric photonic device simulation. We balance the efficiency and generalization of NeurOLight via several novel techniques. Specifically, we discretize different devices into a unified domain, represent parametric PDEs with a compact wave prior, and encode the incident light via masked source modeling. We design our model with parameter-efficient cross-shaped NeurOLight blocks and adopt superposition-based augmentation for data-efficient learning. With these synergistic approaches, NeurOLight generalizes to a large space of unseen simulation settings, demonstrates 2-orders-of-magnitude faster simulation speed than numerical solvers, and outperforms prior neural network models by ~54% lower prediction error with ~44% fewer parameters. Our code is available at https://github.com/JeremieMelo/NeurOLight.