One step closer to unbiased aleatoric uncertainty estimation

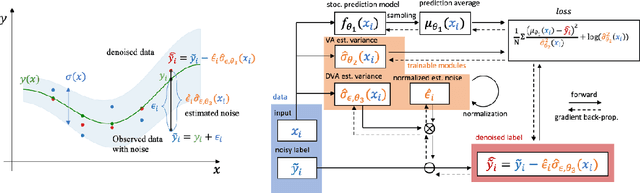
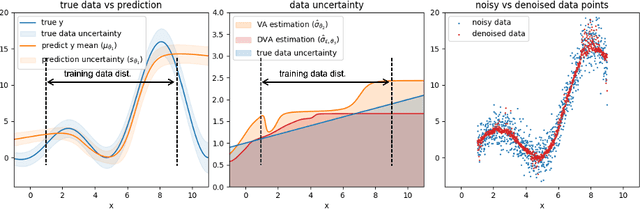
Neural networks are powerful tools in various applications, and quantifying their uncertainty is crucial for reliable decision-making. In the deep learning field, the uncertainties are usually categorized into aleatoric (data) and epistemic (model) uncertainty. In this paper, we point out that the existing popular variance attenuation method highly overestimates aleatoric uncertainty. To address this issue, we propose a new estimation method by actively de-noising the observed data. By conducting a broad range of experiments, we demonstrate that our proposed approach provides a much closer approximation to the actual data uncertainty than the standard method.

ConCerNet: A Contrastive Learning Based Framework for Automated Conservation Law Discovery and Trustworthy Dynamical System Prediction

Deep neural networks (DNN) have shown great capacity of modeling a dynamical system; nevertheless, they usually do not obey physics constraints such as conservation laws. This paper proposes a new learning framework named ConCerNet to improve the trustworthiness of the DNN based dynamics modeling to endow the invariant properties. ConCerNet consists of two steps: (i) a contrastive learning method to automatically capture the system invariants (i.e. conservation properties) along the trajectory observations; (ii) a neural projection layer to guarantee that the learned dynamics models preserve the learned invariants. We theoretically prove the functional relationship between the learned latent representation and the unknown system invariant function. Experiments show that our method consistently outperforms the baseline neural networks in both coordinate error and conservation metrics by a large margin. With neural network based parameterization and no dependence on prior knowledge, our method can be extended to complex and large-scale dynamics by leveraging an autoencoder.

Robust Online Control with Model Misspecification

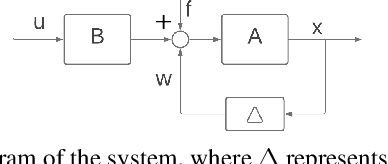
We study online control of an unknown nonlinear dynamical system that is approximated by a time-invariant linear system with model misspecification. Our study focuses on robustness, which measures how much deviation from the assumed linear approximation can be tolerated while maintaining a bounded $\ell_2$-gain compared to the optimal control in hindsight. Some models cannot be stabilized even with perfect knowledge of their coefficients: the robustness is limited by the minimal distance between the assumed dynamics and the set of unstabilizable dynamics. Therefore it is necessary to assume a lower bound on this distance. Under this assumption, and with full observation of the $d$ dimensional state, we describe an efficient controller that attains $\Omega(\frac{1}{\sqrt{d}})$ robustness together with an $\ell_2$-gain whose dimension dependence is near optimal. We also give an inefficient algorithm that attains constant robustness independent of the dimension, with a finite but sub-optimal $\ell_2$-gain.

Convex Parameterizations and Fidelity Bounds for Nonlinear Identification and Reduced-Order Modelling

Model instability and poor prediction of long-term behavior are common problems when modeling dynamical systems using nonlinear "black-box" techniques. Direct optimization of the long-term predictions, often called simulation error minimization, leads to optimization problems that are generally non-convex in the model parameters and suffer from multiple local minima. In this work we present methods which address these problems through convex optimization, based on Lagrangian relaxation, dissipation inequalities, contraction theory, and semidefinite programming. We demonstrate the proposed methods with a model order reduction task for electronic circuit design and the identification of a pneumatic actuator from experiment.