Convex Parameterizations and Fidelity Bounds for Nonlinear Identification and Reduced-Order Modelling

Model instability and poor prediction of long-term behavior are common problems when modeling dynamical systems using nonlinear "black-box" techniques. Direct optimization of the long-term predictions, often called simulation error minimization, leads to optimization problems that are generally non-convex in the model parameters and suffer from multiple local minima. In this work we present methods which address these problems through convex optimization, based on Lagrangian relaxation, dissipation inequalities, contraction theory, and semidefinite programming. We demonstrate the proposed methods with a model order reduction task for electronic circuit design and the identification of a pneumatic actuator from experiment.

Technical Report: Convex Optimization of Nonlinear Feedback Controllers via Occupation Measures

In this paper, we present an approach for designing feedback controllers for polynomial systems that maximize the size of the time-limited backwards reachable set (BRS). We rely on the notion of occupation measures to pose the synthesis problem as an infinite dimensional linear program (LP) and provide finite dimensional approximations of this LP in terms of semidefinite programs (SDPs). The solution to each SDP yields a polynomial control policy and an outer approximation of the largest achievable BRS. In contrast to traditional Lyapunov based approaches which are non-convex and require feasible initialization, our approach is convex and does not require any form of initialization. The resulting time-varying controllers and approximated reachable sets are well-suited for use in a trajectory library or feedback motion planning algorithm. We demonstrate the efficacy and scalability of our approach on five nonlinear systems.

Regions of Attraction for Hybrid Limit Cycles of Walking Robots

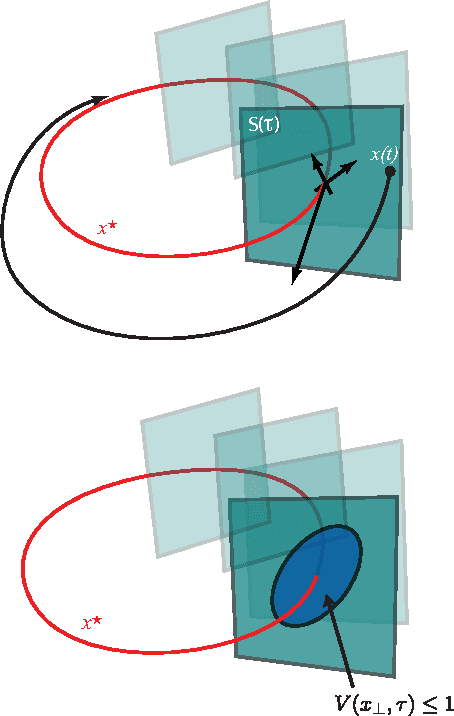
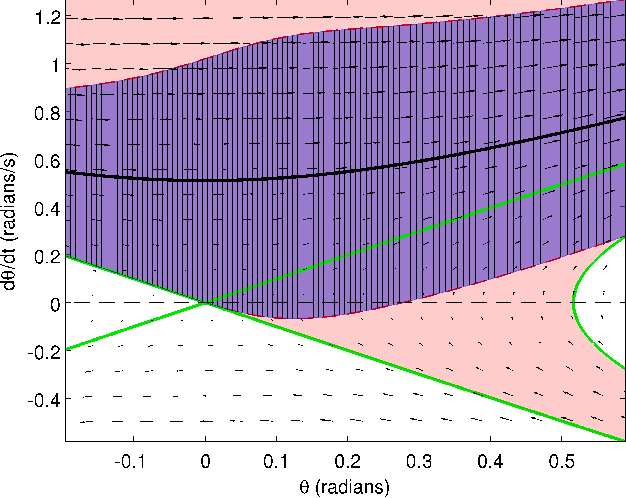
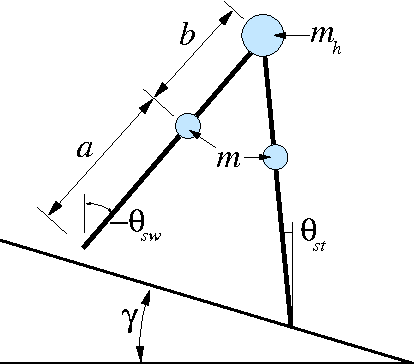
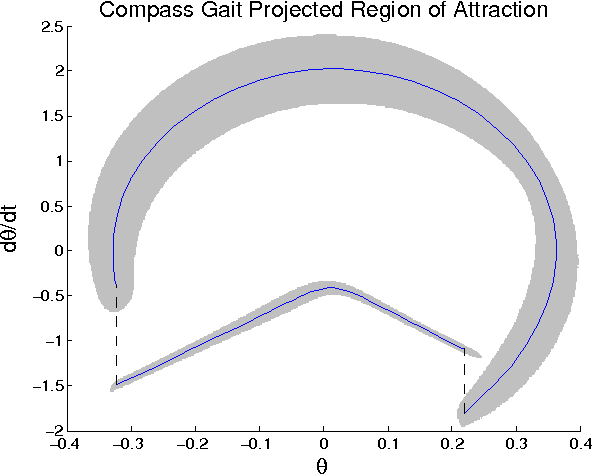
This paper illustrates the application of recent research in region-of-attraction analysis for nonlinear hybrid limit cycles. Three example systems are analyzed in detail: the van der Pol oscillator, the "rimless wheel", and the "compass gait", the latter two being simplified models of underactuated walking robots. The method used involves decomposition of the dynamics about the target cycle into tangential and transverse components, and a search for a Lyapunov function in the transverse dynamics using sum-of-squares analysis (semidefinite programming). Each example illuminates different aspects of the procedure, including optimization of transversal surfaces, the handling of impact maps, optimization of the Lyapunov function, and orbitally-stabilizing control design.