OptiMUS-0.3: Using Large Language Models to Model and Solve Optimization Problems at Scale

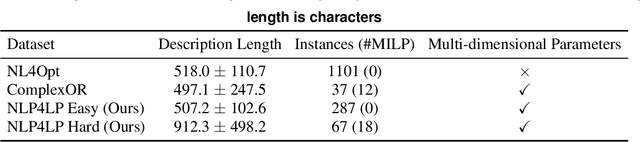
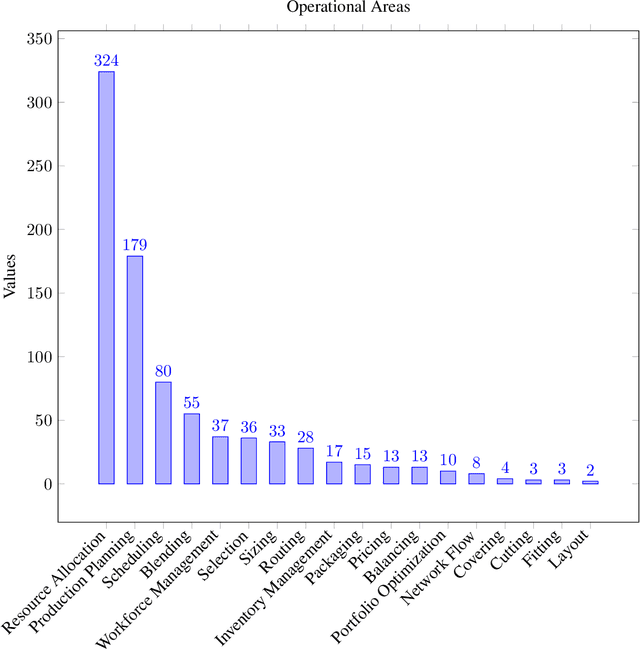
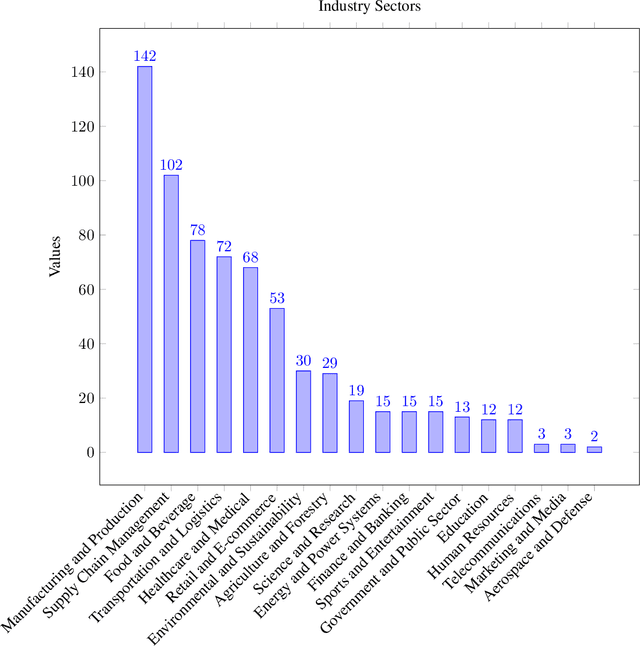
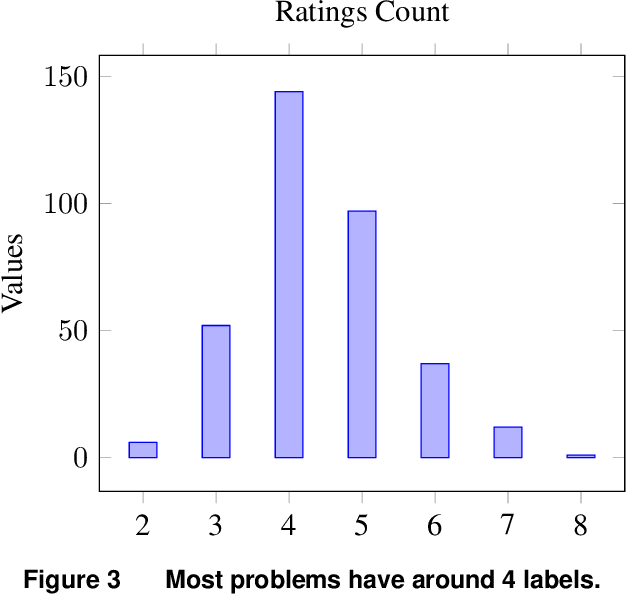
Optimization problems are pervasive in sectors from manufacturing and distribution to healthcare. However, most such problems are still solved heuristically by hand rather than optimally by state-of-the art solvers because the expertise required to formulate and solve these problems limits the widespread adoption of optimization tools and techniques. We introduce a Large Language Model (LLM)-based system designed to formulate and solve (mixed integer) linear programming problems from their natural language descriptions. Our system is capable of developing mathematical models, writing and debugging solver code, evaluating the generated solutions, and improving efficiency and correctness of its model and code based on these evaluations. OptiMUS-0.3 utilizes a modular structure to process problems, allowing it to handle problems with long descriptions and complex data without long prompts. Experiments demonstrate that OptiMUS-0.3 outperforms existing state-of-the-art methods on easy datasets by more than 12% and on hard datasets (including a new dataset, NLP4LP, released with this paper that features long and complex problems) by more than 8%.

OptiMUS: Scalable Optimization Modeling with (MI)LP Solvers and Large Language Models

Optimization problems are pervasive in sectors from manufacturing and distribution to healthcare. However, most such problems are still solved heuristically by hand rather than optimally by state-of-the-art solvers because the expertise required to formulate and solve these problems limits the widespread adoption of optimization tools and techniques. This paper introduces OptiMUS, a Large Language Model (LLM)-based agent designed to formulate and solve (mixed integer) linear programming problems from their natural language descriptions. OptiMUS can develop mathematical models, write and debug solver code, evaluate the generated solutions, and improve its model and code based on these evaluations. OptiMUS utilizes a modular structure to process problems, allowing it to handle problems with long descriptions and complex data without long prompts. Experiments demonstrate that OptiMUS outperforms existing state-of-the-art methods on easy datasets by more than $20\%$ and on hard datasets (including a new dataset, NLP4LP, released with this paper that features long and complex problems) by more than $30\%$.

OptiMUS: Optimization Modeling Using mip Solvers and large language models

Optimization problems are pervasive across various sectors, from manufacturing and distribution to healthcare. However, most such problems are still solved heuristically by hand rather than optimally by state-of-the-art solvers, as the expertise required to formulate and solve these problems limits the widespread adoption of optimization tools and techniques. We introduce OptiMUS, a Large Language Model (LLM)-based agent designed to formulate and solve MILP problems from their natural language descriptions. OptiMUS is capable of developing mathematical models, writing and debugging solver code, developing tests, and checking the validity of generated solutions. To benchmark our agent, we present NLP4LP, a novel dataset of linear programming (LP) and mixed integer linear programming (MILP) problems. Our experiments demonstrate that OptiMUS is able to solve 67\% more problems compared to a basic LLM prompting strategy. OptiMUS code and NLP4LP dataset are available at \href{https://github.com/teshnizi/OptiMUS}{https://github.com/teshnizi/OptiMUS}

LazyIter: A Fast Algorithm for Counting Markov Equivalent DAGs and Designing Experiments

The causal relationships among a set of random variables are commonly represented by a Directed Acyclic Graph (DAG), where there is a directed edge from variable $X$ to variable $Y$ if $X$ is a direct cause of $Y$. From the purely observational data, the true causal graph can be identified up to a Markov Equivalence Class (MEC), which is a set of DAGs with the same conditional independencies between the variables. The size of an MEC is a measure of complexity for recovering the true causal graph by performing interventions. We propose a method for efficient iteration over possible MECs given intervention results. We utilize the proposed method for computing MEC sizes and experiment design in active and passive learning settings. Compared to previous work for computing the size of MEC, our proposed algorithm reduces the time complexity by a factor of $O(n)$ for sparse graphs where $n$ is the number of variables in the system. Additionally, integrating our approach with dynamic programming, we design an optimal algorithm for passive experiment design. Experimental results show that our proposed algorithms for both computing the size of MEC and experiment design outperform the state of the art.