Jackknife Variability Estimation For Randomized Matrix Computations

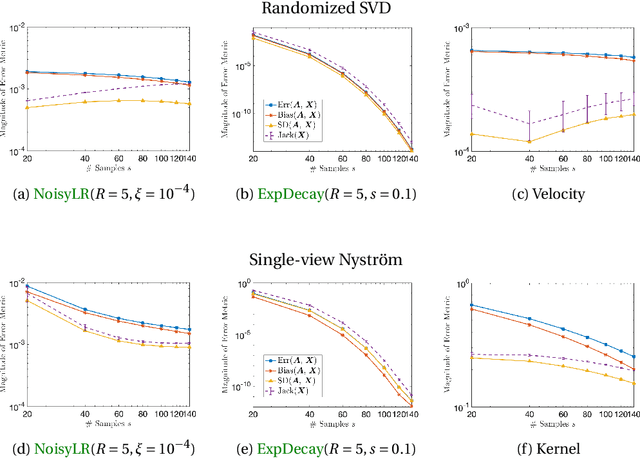
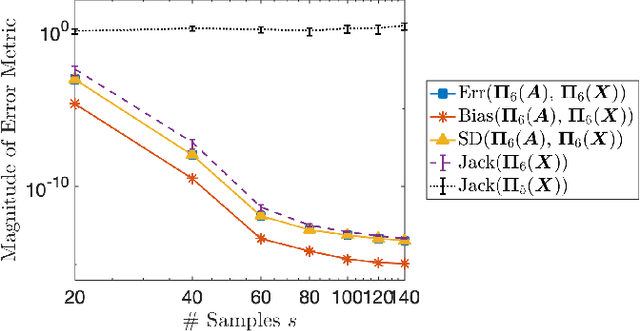
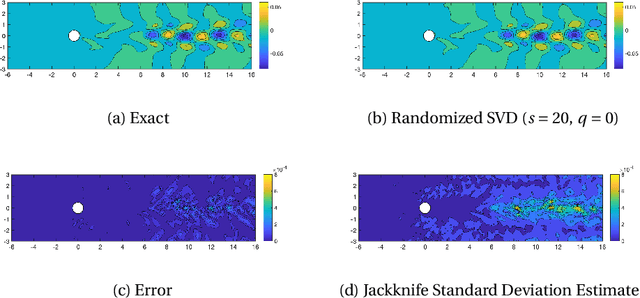
Randomized algorithms based on sketching have become a workhorse tool in low-rank matrix approximation. To use these algorithms safely in applications, they should be coupled with diagnostics to assess the quality of approximation. To meet this need, this paper proposes a jackknife resampling method to estimate the variability of the output of a randomized matrix computation. The variability estimate can recognize that a computation requires additional data or that the computation is intrinsically unstable. As examples, the paper studies jackknife estimates for two randomized low-rank matrix approximation algorithms. In each case, the operation count for the jackknife estimate is independent of the dimensions of the target matrix. In numerical experiments, the estimator accurately assesses variability and also provides an order-of-magnitude estimate of the mean-square error.