Dynamic Structure Estimation from Bandit Feedback
Paper and Code
Jun 02, 2022
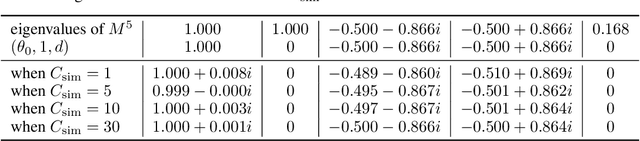
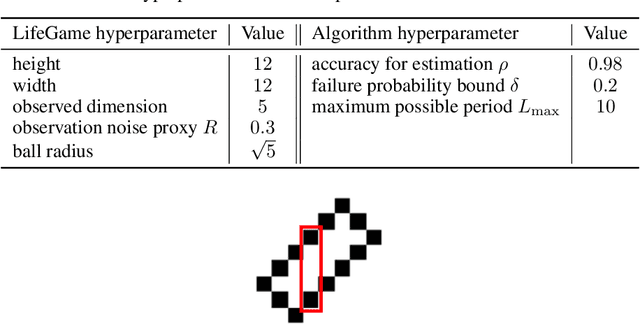
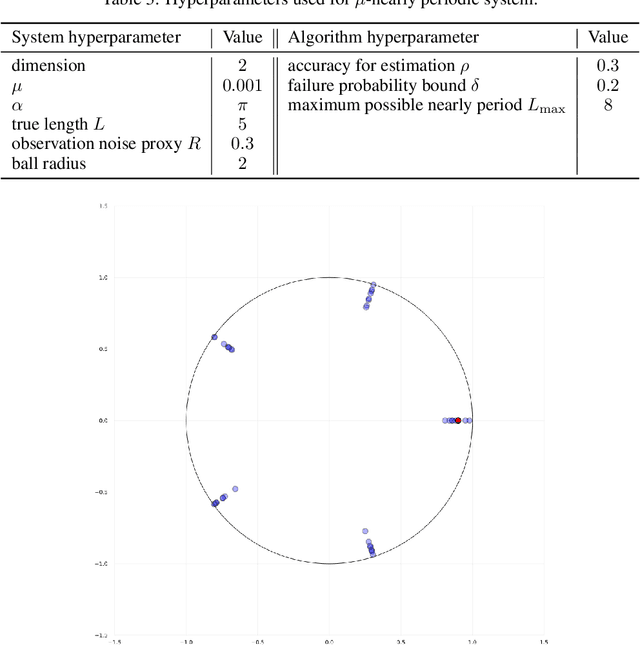
This work present novel method for structure estimation of an underlying dynamical system. We tackle problems of estimating dynamic structure from bandit feedback contaminated by sub-Gaussian noise. In particular, we focus on periodically behaved discrete dynamical system in the Euclidean space, and carefully identify certain obtainable subset of full information of the periodic structure. We then derive a sample complexity bound for periodic structure estimation. Technically, asymptotic results for exponential sums are adopted to effectively average out the noise effects while preventing the information to be estimated from vanishing. For linear systems, the use of the Weyl sum further allows us to extract eigenstructures. Our theoretical claims are experimentally validated on simulations of toy examples, including Cellular Automata.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge