Monotone Lipschitz-Gradient Denoiser: Explainability of Operator Regularization Approaches and Convergence to Optimal Point

This paper addresses explainability of the operator-regularization approach under the use of monotone Lipschitz-gradient (MoL-Grad) denoiser -- an operator that can be expressed as the Lipschitz continuous gradient of a differentiable convex function. We prove that an operator is a MoL-Grad denoiser if and only if it is the ``single-valued'' proximity operator of a weakly convex function. An extension of Moreau's decomposition is also shown with respect to a weakly convex function and the conjugate of its convexified function. Under these arguments, two specific algorithms, the forward-backward splitting algorithm and the primal-dual splitting algorithm, are considered, both employing MoL-Grad denoisers. These algorithms generate a sequence of vectors converging weakly, under conditions, to a minimizer of a certain cost function which involves an ``implicit regularizer'' induced by the denoiser. The theoretical findings are supported by simulations.

Computing an Entire Solution Path of a Nonconvexly Regularized Convex Sparse Model

The generalized minimax concave (GMC) penalty is a nonconvex sparse regularizer which can preserve the overall-convexity of the sparse least squares problem. In this paper, we study the solution path of a special but important instance of the GMC model termed the scaled GMC (sGMC) model. We show that despite the nonconvexity of the regularizer, there exists a solution path of the sGMC model which is piecewise linear as a function of the tuning parameter, and we propose an efficient algorithm for computing a solution path of this type. Our algorithm is an extension of the well-known least angle regression (LARS) algorithm for LASSO, hence we term the proposed algorithm LARS-sGMC. Under suitable conditions, we provide a proof of the correctness and finite termination of the proposed LARS-sGMC algorithm. This article also serves as an appendix for the short paper titled ``COMPUTING AN ENTIRE SOLUTION PATH OF A NONCONVEXLY REGULARIZED CONVEX SPARSE MODEL", and addresses proofs and technical derivations that were omitted in the original paper due to space limitation.

A Unified Framework for Solving a General Class of Nonconvexly Regularized Convex Models

Recently, several nonconvex sparse regularizers which can preserve the convexity of the cost function have received increasing attention. This paper proposes a general class of such convexity-preserving (CP) regularizers, termed partially smoothed difference-of-convex (pSDC) regularizer. The pSDC regularizer is formulated as a structured difference-of-convex (DC) function, where the landscape of the subtrahend function can be adjusted by a parameterized smoothing function so as to attain overall-convexity. Assigned with proper building blocks, the pSDC regularizer reproduces existing CP regularizers and opens the way to a large number of promising new ones. With respect to the resultant nonconvexly regularized convex (NRC) model, we derive a series of overall-convexity conditions which naturally embrace the conditions in previous works. Moreover, we develop a unified framework based on DC programming for solving the NRC model. Compared to previously reported proximal splitting type approaches, the proposed framework makes less stringent assumptions. We establish the convergence of the proposed framework to a global minimizer. Numerical experiments demonstrate the power of the pSDC regularizers and the efficiency of the proposed DC algorithm.

Linearly-involved Moreau-Enhanced-over-Subspace Model: Debiased Sparse Modeling and Stable Outlier-Robust Regression

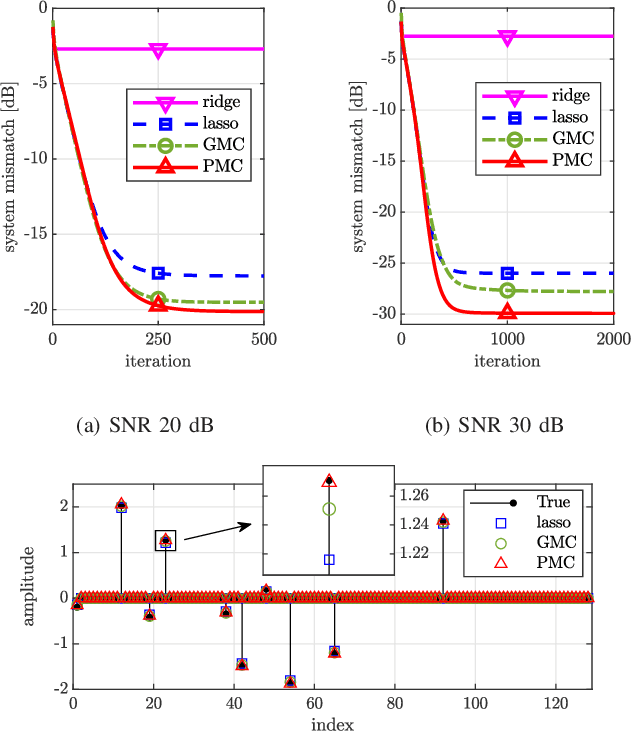
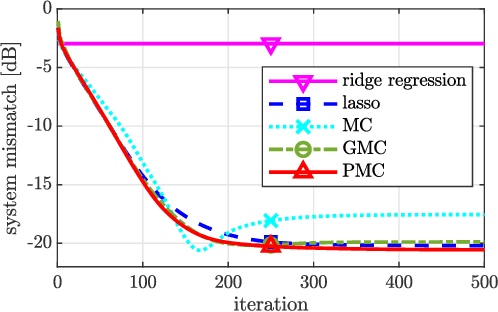
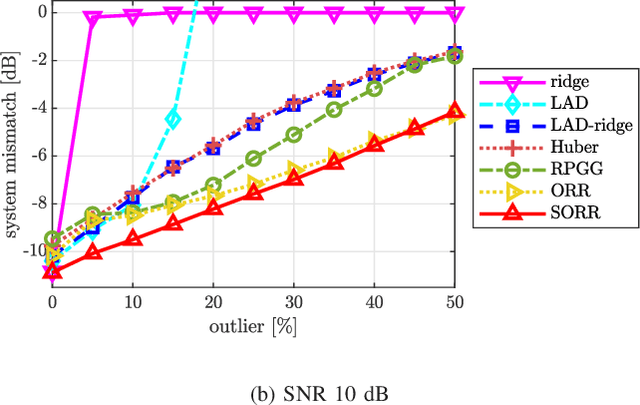
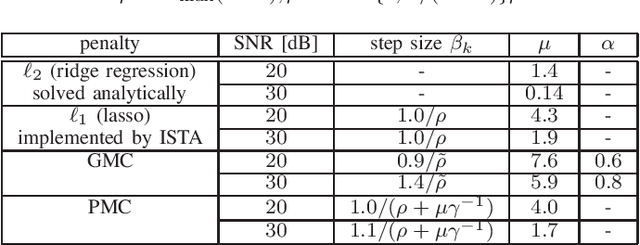
We present an efficient mathematical framework based on the linearly-involved Moreau-enhanced-over-subspace (LiMES) model. Two concrete applications are considered: sparse modeling and robust regression. The popular minimax concave (MC) penalty for sparse modeling subtracts, from the $\ell_1$ norm, its Moreau envelope, inducing nearly unbiased estimates and thus yielding remarkable performance enhancements. To extend it to underdetermined linear systems, we propose the projective minimax concave penalty using the projection onto the input subspace, where the Moreau-enhancement effect is restricted to the subspace for preserving the overall convexity. We also present a novel concept of stable outlier-robust regression which distinguishes noise and outlier explicitly. The LiMES model encompasses those two specific examples as well as two other applications: stable principal component pursuit and robust classification. The LiMES function involved in the model is an ``additively nonseparable'' weakly convex function but is defined with the Moreau envelope returning the minimum of a ``separable'' convex function. This mixed nature of separability and nonseparability allows an application of the LiMES model to the underdetermined case with an efficient algorithmic implementation. Two linear/affine operators play key roles in the model: one corresponds to the projection mentioned above and the other takes care of robust regression/classification. A necessary and sufficient condition for convexity of the smooth part of the objective function is studied. Numerical examples show the efficacy of LiMES in applications to sparse modeling and robust regression.

A Convexly Constrained LiGME Model and Its Proximal Splitting Algorithm

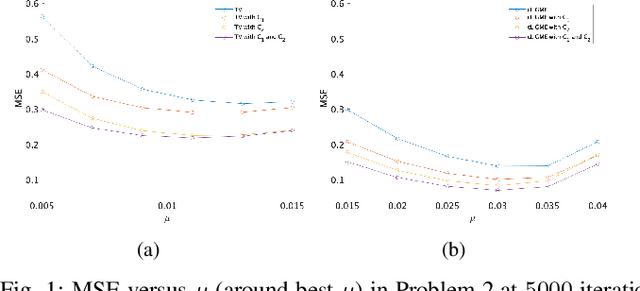
For the sparsity-rank-aware least squares estimations, the LiGME (Linearly involved Generalized Moreau Enhanced) model was established recently in [Abe, Yamagishi, Yamada, 2020] to use certain nonconvex enhancements of linearly involved convex regularizers without losing their overall convexities. In this paper, for further advancement of the LiGME model by incorporating multiple a priori knowledge as hard convex constraints, we newly propose a convexly constrained LiGME (cLiGME) model. The cLiGME model can utilize multiple convex constraints while preserving benefits achieved by the LiGME model. We also present a proximal splitting type algorithm for the proposed cLiGME model. Numerical experiments demonstrate the efficacy of the proposed model and the proposed optimization algorithm in a scenario of signal processing application.

The adaptive projected subgradient method constrained by families of quasi-nonexpansive mappings and its application to online learning

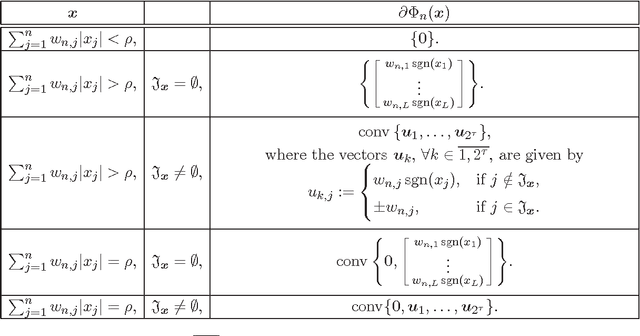
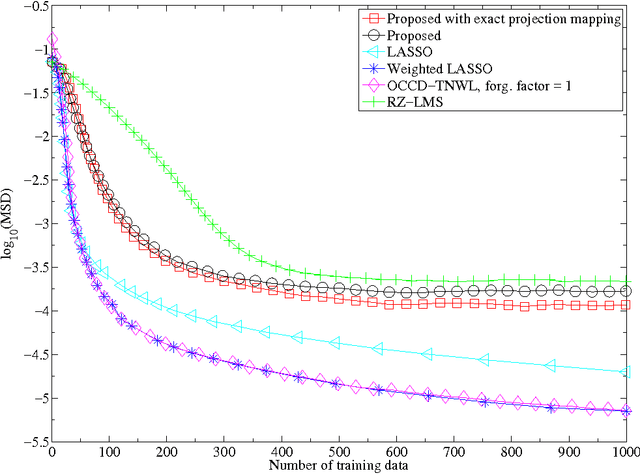
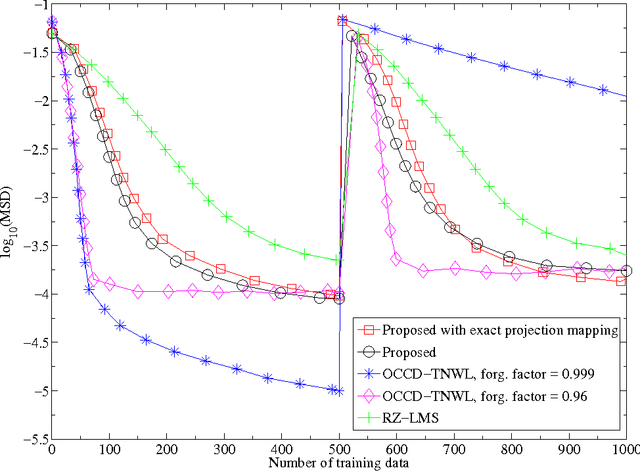
Many online, i.e., time-adaptive, inverse problems in signal processing and machine learning fall under the wide umbrella of the asymptotic minimization of a sequence of non-negative, convex, and continuous functions. To incorporate a-priori knowledge into the design, the asymptotic minimization task is usually constrained on a fixed closed convex set, which is dictated by the available a-priori information. To increase versatility towards the usage of the available information, the present manuscript extends the Adaptive Projected Subgradient Method (APSM) by introducing an algorithmic scheme which incorporates a-priori knowledge in the design via a sequence of strongly attracting quasi-nonexpansive mappings in a real Hilbert space. In such a way, the benefits offered to online learning tasks by the proposed method unfold in two ways: 1) the rich class of quasi-nonexpansive mappings provides a plethora of ways to cast a-priori knowledge, and 2) by introducing a sequence of such mappings, the proposed scheme is able to capture the time-varying nature of a-priori information. The convergence properties of the algorithm are studied, several special cases of the method with wide applicability are shown, and the potential of the proposed scheme is demonstrated by considering an increasingly important, nowadays, online sparse system/signal recovery task.