The adaptive projected subgradient method constrained by families of quasi-nonexpansive mappings and its application to online learning

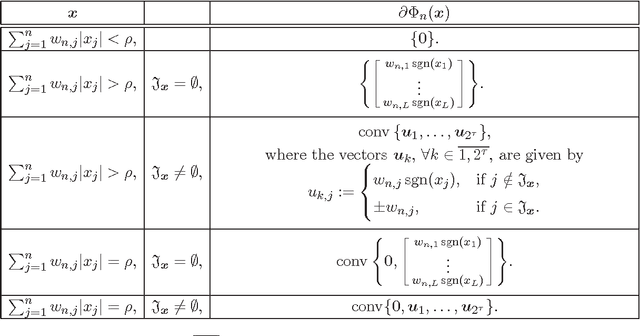
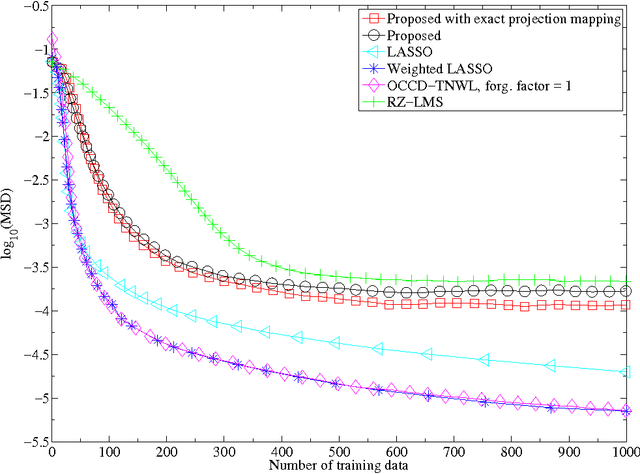
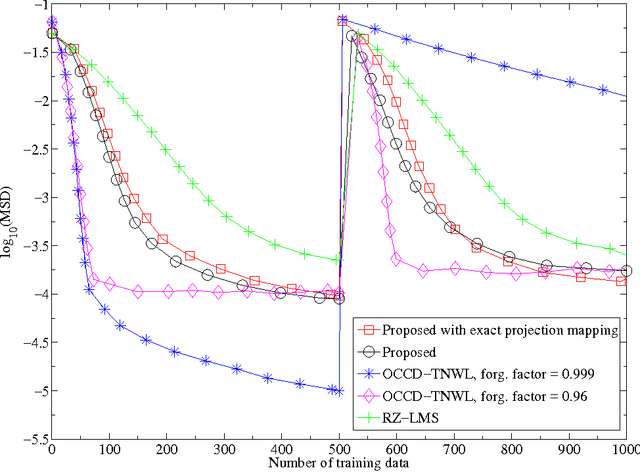
Many online, i.e., time-adaptive, inverse problems in signal processing and machine learning fall under the wide umbrella of the asymptotic minimization of a sequence of non-negative, convex, and continuous functions. To incorporate a-priori knowledge into the design, the asymptotic minimization task is usually constrained on a fixed closed convex set, which is dictated by the available a-priori information. To increase versatility towards the usage of the available information, the present manuscript extends the Adaptive Projected Subgradient Method (APSM) by introducing an algorithmic scheme which incorporates a-priori knowledge in the design via a sequence of strongly attracting quasi-nonexpansive mappings in a real Hilbert space. In such a way, the benefits offered to online learning tasks by the proposed method unfold in two ways: 1) the rich class of quasi-nonexpansive mappings provides a plethora of ways to cast a-priori knowledge, and 2) by introducing a sequence of such mappings, the proposed scheme is able to capture the time-varying nature of a-priori information. The convergence properties of the algorithm are studied, several special cases of the method with wide applicability are shown, and the potential of the proposed scheme is demonstrated by considering an increasingly important, nowadays, online sparse system/signal recovery task.