An LiGME Regularizer of Designated Isolated Minimizers -- An Application to Discrete-Valued Signal Estimation

For a regularized least squares estimation of discrete-valued signals, we propose an LiGME regularizer, as a nonconvex regularizer, of designated isolated minimizers. The proposed regularizer is designed as a Generalized Moreau Enhancement (GME) of the so-called SOAV convex regularizer. Every candidate vector in the discrete-valued set is aimed to be assigned to an isolated local minimizer of the proposed regularizer while the overall convexity of the regularized least squares model is maintained. Moreover, a global minimizer of the proposed model can be approximated iteratively by using a variant of cLiGME algorithm. To enhance the accuracy of the proposed estimation, we also propose a pair of simple modifications, called respectively an iterative reweighting and a generalized superiorization. Numerical experiments demonstrate the effectiveness of the proposed model and algorithms in a scenario of MIMO signal detection.

A Convexly Constrained LiGME Model and Its Proximal Splitting Algorithm

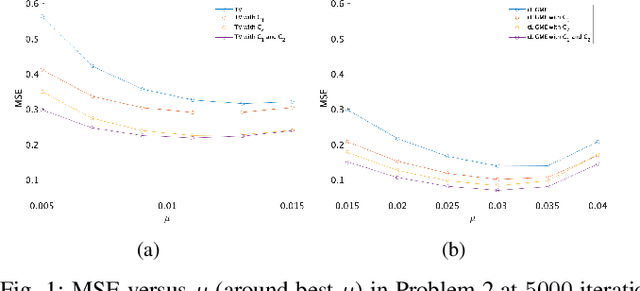
For the sparsity-rank-aware least squares estimations, the LiGME (Linearly involved Generalized Moreau Enhanced) model was established recently in [Abe, Yamagishi, Yamada, 2020] to use certain nonconvex enhancements of linearly involved convex regularizers without losing their overall convexities. In this paper, for further advancement of the LiGME model by incorporating multiple a priori knowledge as hard convex constraints, we newly propose a convexly constrained LiGME (cLiGME) model. The cLiGME model can utilize multiple convex constraints while preserving benefits achieved by the LiGME model. We also present a proximal splitting type algorithm for the proposed cLiGME model. Numerical experiments demonstrate the efficacy of the proposed model and the proposed optimization algorithm in a scenario of signal processing application.