Adaptive Learning in Cartesian Product of Reproducing Kernel Hilbert Spaces
Paper and Code
Nov 05, 2014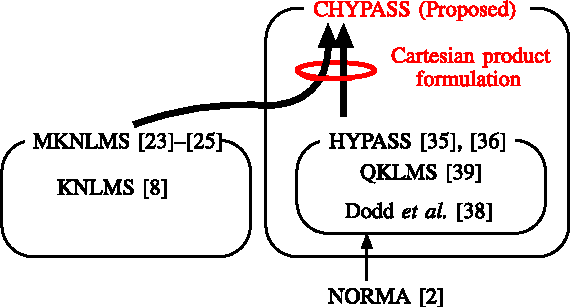
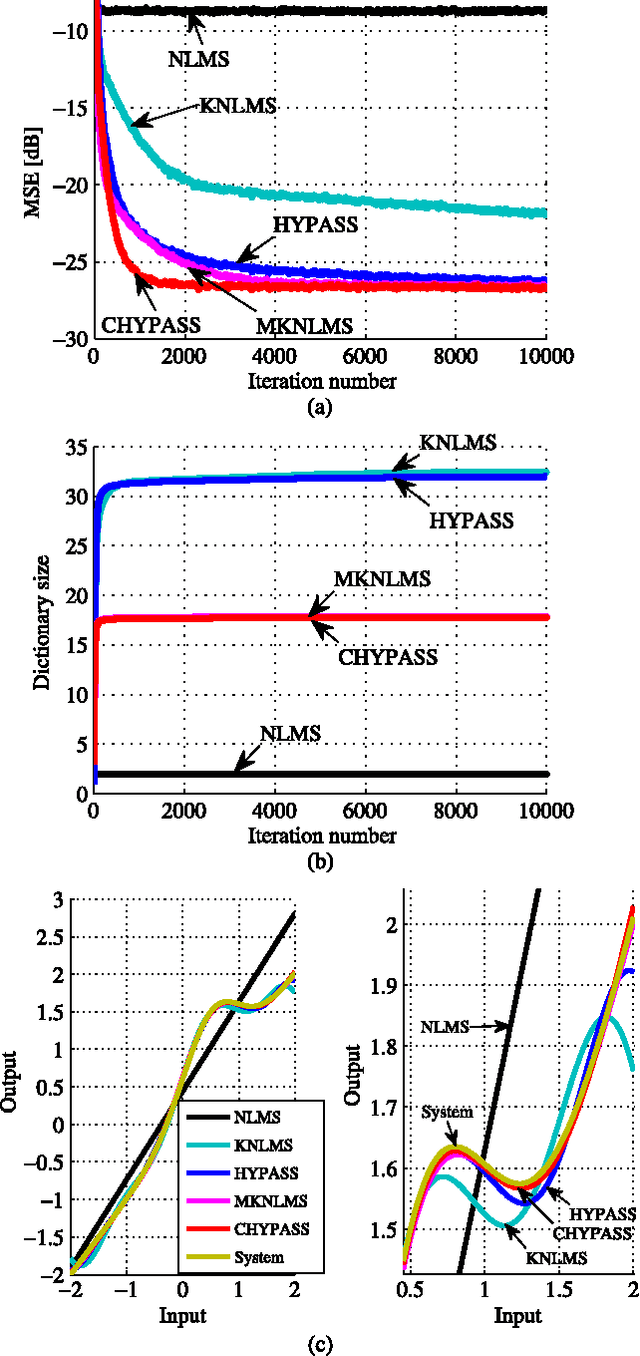
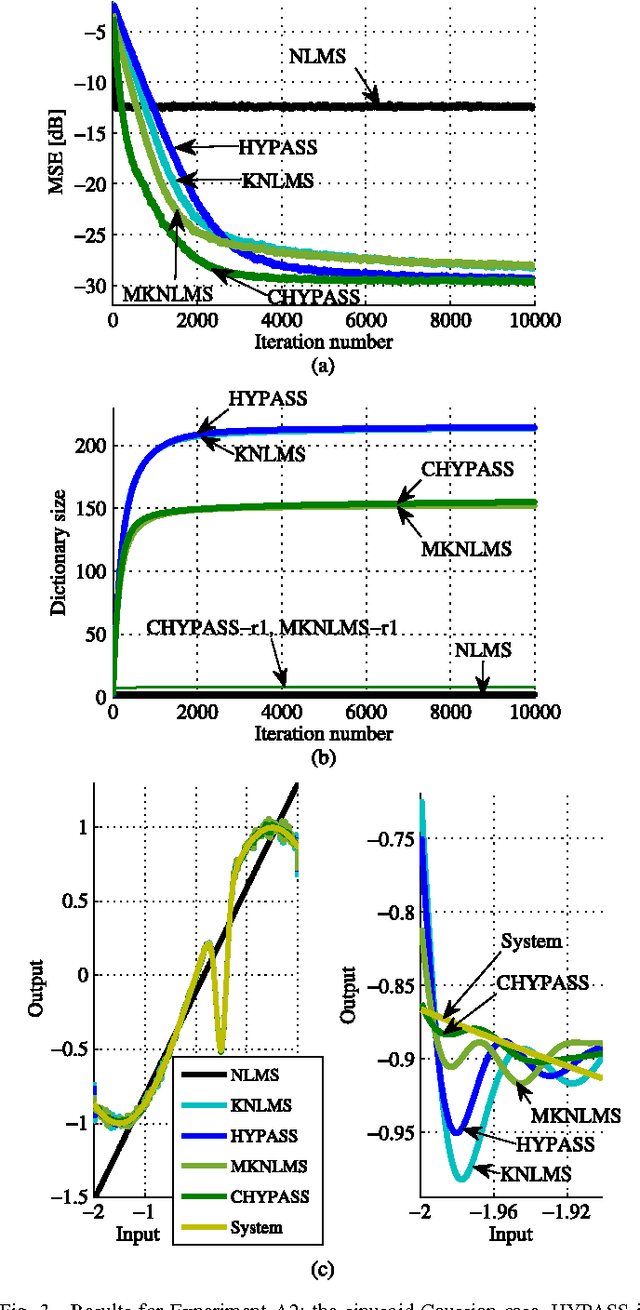
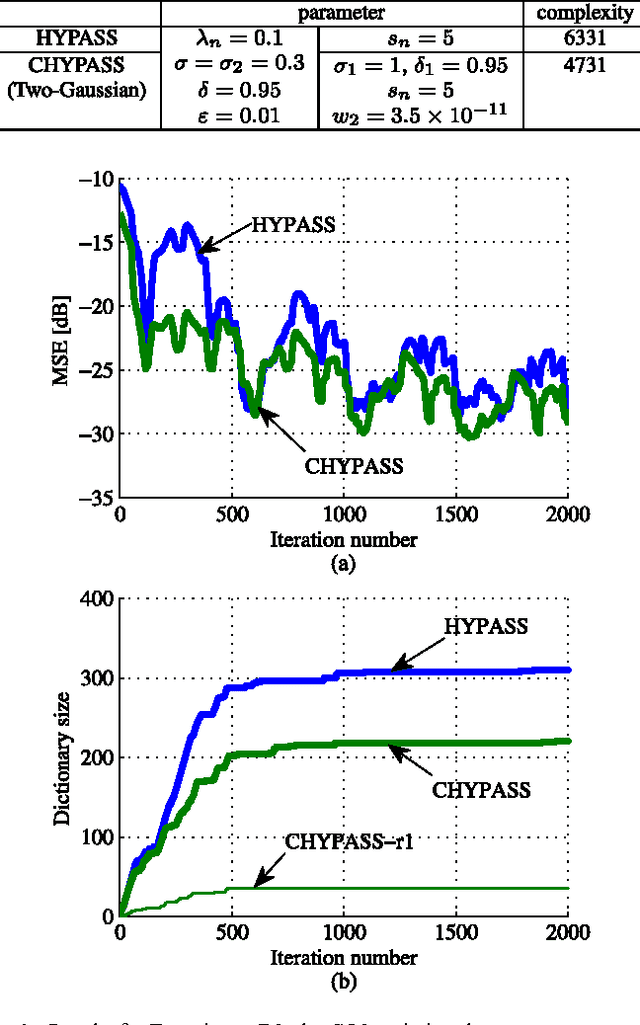
We propose a novel adaptive learning algorithm based on iterative orthogonal projections in the Cartesian product of multiple reproducing kernel Hilbert spaces (RKHSs). The task is estimating/tracking nonlinear functions which are supposed to contain multiple components such as (i) linear and nonlinear components, (ii) high- and low- frequency components etc. In this case, the use of multiple RKHSs permits a compact representation of multicomponent functions. The proposed algorithm is where two different methods of the author meet: multikernel adaptive filtering and the algorithm of hyperplane projection along affine subspace (HYPASS). In a certain particular case, the sum space of the RKHSs is isomorphic to the product space and hence the proposed algorithm can also be regarded as an iterative projection method in the sum space. The efficacy of the proposed algorithm is shown by numerical examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge