Structure Learning of Sparse GGMs over Multiple Access Networks

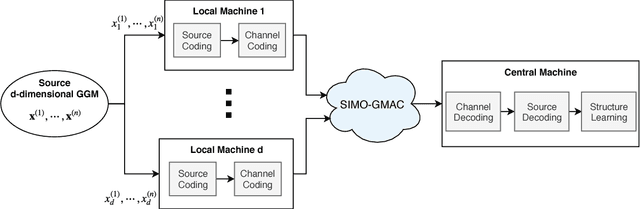
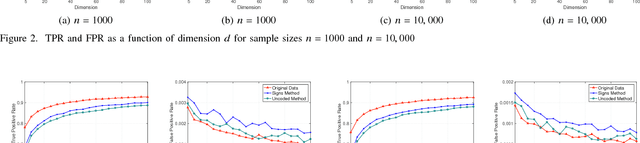
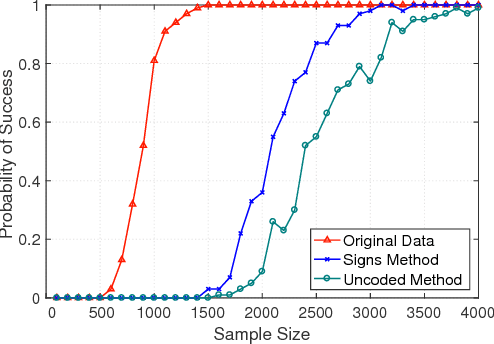
A central machine is interested in estimating the underlying structure of a sparse Gaussian Graphical Model (GGM) from datasets distributed across multiple local machines. The local machines can communicate with the central machine through a wireless multiple access channel. In this paper, we are interested in designing effective strategies where reliable learning is feasible under power and bandwidth limitations. Two approaches are proposed: Signs and Uncoded methods. In Signs method, the local machines quantize their data into binary vectors and an optimal channel coding scheme is used to reliably send the vectors to the central machine where the structure is learned from the received data. In Uncoded method, data symbols are scaled and transmitted through the channel. The central machine uses the received noisy symbols to recover the structure. Theoretical results show that both methods can recover the structure with high probability for large enough sample size. Experimental results indicate the superiority of Signs method over Uncoded method under several circumstances.

Learning of Tree-Structured Gaussian Graphical Models on Distributed Data under Communication Constraints

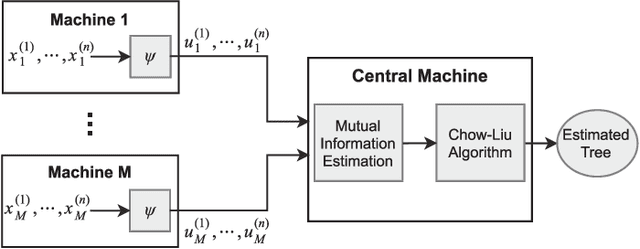
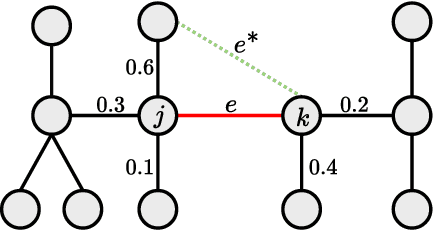
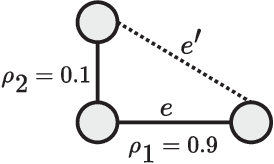
In this paper, learning of tree-structured Gaussian graphical models from distributed data is addressed. In our model, samples are stored in a set of distributed machines where each machine has access to only a subset of features. A central machine is then responsible for learning the structure based on received messages from the other nodes. We present a set of communication efficient strategies, which are theoretically proved to convey sufficient information for reliable learning of the structure. In particular, our analyses show that even if each machine sends only the signs of its local data samples to the central node, the tree structure can still be recovered with high accuracy. Our simulation results on both synthetic and real-world datasets show that our strategies achieve a desired accuracy in inferring the underlying structure, while spending a small budget on communication.

Learning of Gaussian Processes in Distributed and Communication Limited Systems

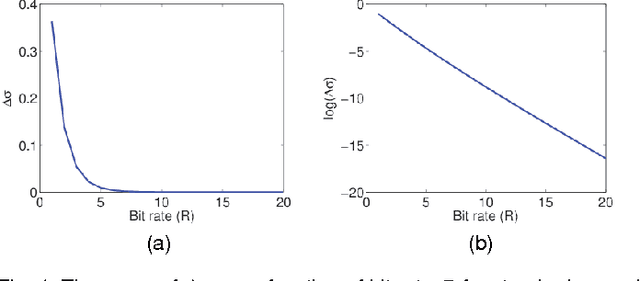
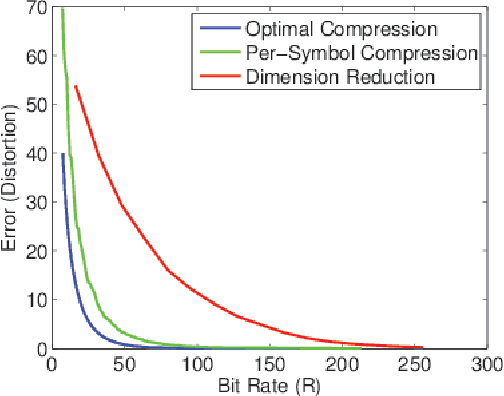
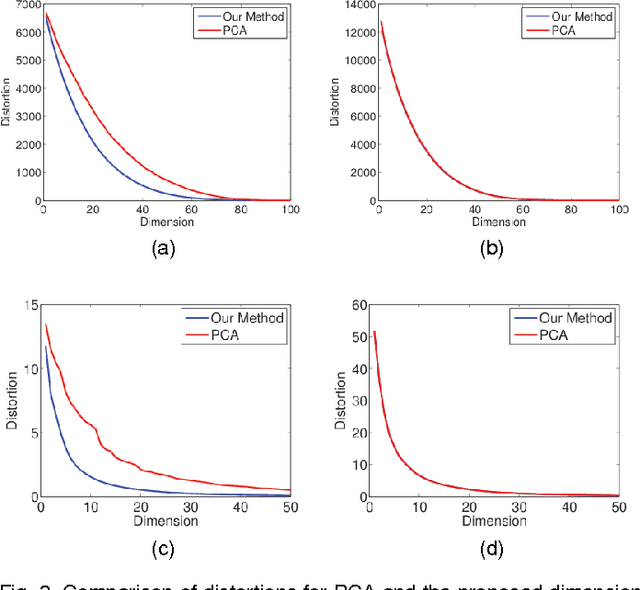
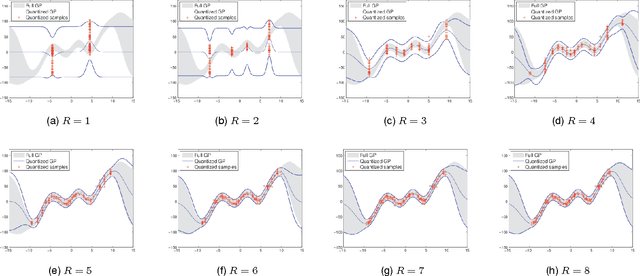
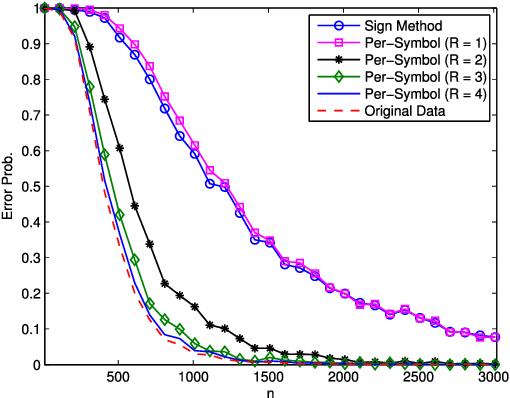
It is of fundamental importance to find algorithms obtaining optimal performance for learning of statistical models in distributed and communication limited systems. Aiming at characterizing the optimal strategies, we consider learning of Gaussian Processes (GPs) in distributed systems as a pivotal example. We first address a very basic problem: how many bits are required to estimate the inner-products of Gaussian vectors across distributed machines? Using information theoretic bounds, we obtain an optimal solution for the problem which is based on vector quantization. Two suboptimal and more practical schemes are also presented as substitute for the vector quantization scheme. In particular, it is shown that the performance of one of the practical schemes which is called per-symbol quantization is very close to the optimal one. Schemes provided for the inner-product calculations are incorporated into our proposed distributed learning methods for GPs. Experimental results show that with spending few bits per symbol in our communication scheme, our proposed methods outperform previous zero rate distributed GP learning schemes such as Bayesian Committee Model (BCM) and Product of experts (PoE).