Efficient learning of differential network in multi-source non-paranormal graphical models

This paper addresses learning of sparse structural changes or differential network between two classes of non-paranormal graphical models. We assume a multi-source and heterogeneous dataset is available for each class, where the covariance matrices are identical for all non-paranormal graphical models. The differential network, which are encoded by the difference precision matrix, can then be decoded by optimizing a lasso penalized D-trace loss function. To this aim, an efficient approach is proposed that outputs the exact solution path, outperforming the previous methods that only sample from the solution path in pre-selected regularization parameters. Notably, our proposed method has low computational complexity, especially when the differential network are sparse. Our simulations on synthetic data demonstrate a superior performance for our strategy in terms of speed and accuracy compared to an existing method. Moreover, our strategy in combining datasets from multiple sources is shown to be very effective in inferring differential network in real-world problems. This is backed by our experimental results on drug resistance in tumor cancers. In the latter case, our strategy outputs important genes for drug resistance which are already confirmed by various independent studies.

Sample Complexity Bounds for Learning High-dimensional Simplices in Noisy Regimes

In this paper, we propose a sample complexity bound for learning a simplex from noisy samples. A dataset of size $n$ is given which includes i.i.d. samples drawn from a uniform distribution over an unknown arbitrary simplex in $\mathbb{R}^K$, where samples are assumed to be corrupted by an additive Gaussian noise of an arbitrary magnitude. We propose a strategy which outputs a simplex having, with high probability, a total variation distance of $\epsilon + O\left(\mathrm{SNR}^{-1}\right)$ from the true simplex, for any $\epsilon>0$. We prove that to arrive this close to the true simplex, it is sufficient to have $n\ge\tilde{O}\left(K^2/\epsilon^2\right)$ samples. Here, SNR stands for the signal-to-noise ratio which can be viewed as the ratio of the diameter of the simplex to the standard deviation of the noise. Our proofs are based on recent advancements in sample compression techniques, which have already shown promises in deriving tight bounds for density estimation in high-dimensional Gaussian mixture models.

Isoform Function Prediction Using Deep Neural Network

Isoforms are mRNAs produced from the same gene site in the phenomenon called Alternative Splicing. Studies have shown that more than 95% of human multi-exon genes have undergone alternative splicing. Although there are few changes in mRNA sequence, They may have a systematic effect on cell function and regulation. It is widely reported that isoforms of a gene have distinct or even contrasting functions. Most studies have shown that alternative splicing plays a significant role in human health and disease. Despite the wide range of gene function studies, there is little information about isoforms' functionalities. Recently, some computational methods based on Multiple Instance Learning have been proposed to predict isoform function using gene function and gene expression profile. However, their performance is not desirable due to the lack of labeled training data. In addition, probabilistic models such as Conditional Random Field (CRF) have been used to model the relation between isoforms. This project uses all the data and valuable information such as isoform sequences, expression profiles, and gene ontology graphs and proposes a comprehensive model based on Deep Neural Networks. The UniProt Gene Ontology (GO) database is used as a standard reference for gene functions. The NCBI RefSeq database is used for extracting gene and isoform sequences, and the NCBI SRA database is used for expression profile data. Metrics such as Receiver Operating Characteristic Area Under the Curve (ROC AUC) and Precision-Recall Under the Curve (PR AUC) are used to measure the prediction accuracy.

Distributed Sparse Feature Selection in Communication-Restricted Networks

This paper aims to propose and theoretically analyze a new distributed scheme for sparse linear regression and feature selection. The primary goal is to learn the few causal features of a high-dimensional dataset based on noisy observations from an unknown sparse linear model. However, the presumed training set which includes $n$ data samples in $\mathbb{R}^p$ is already distributed over a large network with $N$ clients connected through extremely low-bandwidth links. Also, we consider the asymptotic configuration of $1\ll N\ll n\ll p$. In order to infer the causal dimensions from the whole dataset, we propose a simple, yet effective method for information sharing in the network. In this regard, we theoretically show that the true causal features can be reliably recovered with negligible bandwidth usage of $O\left(N\log p\right)$ across the network. This yields a significantly lower communication cost in comparison with the trivial case of transmitting all the samples to a single node (centralized scenario), which requires $O\left(np\right)$ transmissions. Even more sophisticated schemes such as ADMM still have a communication complexity of $O\left(Np\right)$. Surprisingly, our sample complexity bound is proved to be the same (up to a constant factor) as the optimal centralized approach for a fixed performance measure in each node, while that of a na\"{i}ve decentralized technique grows linearly with $N$. Theoretical guarantees in this paper are based on the recent analytic framework of debiased LASSO in Javanmard et al. (2019), and are supported by several computer experiments performed on both synthetic and real-world datasets.

Regularizing Recurrent Neural Networks via Sequence Mixup

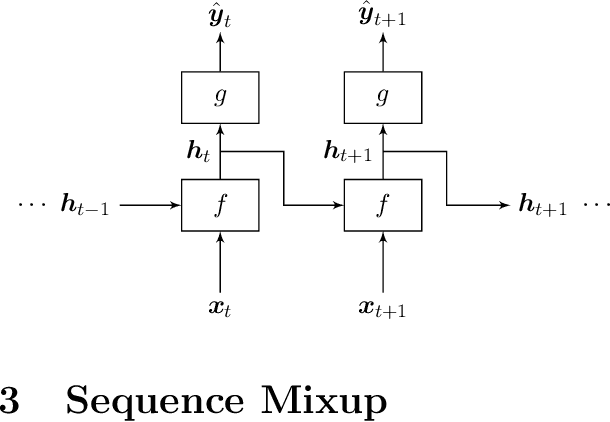
In this paper, we extend a class of celebrated regularization techniques originally proposed for feed-forward neural networks, namely Input Mixup (Zhang et al., 2017) and Manifold Mixup (Verma et al., 2018), to the realm of Recurrent Neural Networks (RNN). Our proposed methods are easy to implement and have a low computational complexity, while leverage the performance of simple neural architectures in a variety of tasks. We have validated our claims through several experiments on real-world datasets, and also provide an asymptotic theoretical analysis to further investigate the properties and potential impacts of our proposed techniques. Applying sequence mixup to BiLSTM-CRF model (Huang et al., 2015) to Named Entity Recognition task on CoNLL-2003 data (Sang and De Meulder, 2003) has improved the F-1 score on the test stage and reduced the loss, considerably.

Structure Learning of Sparse GGMs over Multiple Access Networks

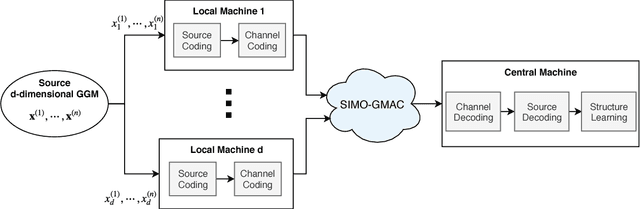
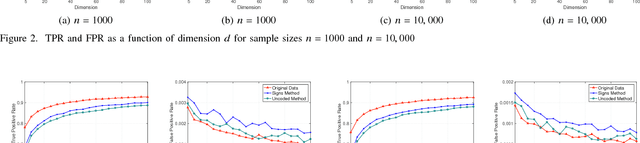
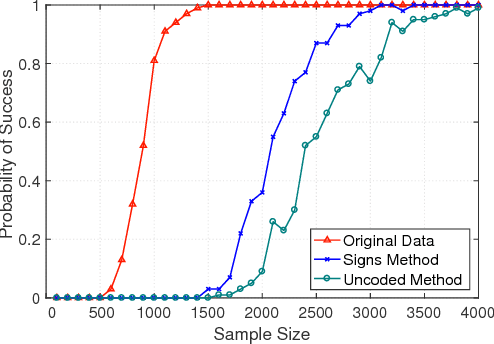
A central machine is interested in estimating the underlying structure of a sparse Gaussian Graphical Model (GGM) from datasets distributed across multiple local machines. The local machines can communicate with the central machine through a wireless multiple access channel. In this paper, we are interested in designing effective strategies where reliable learning is feasible under power and bandwidth limitations. Two approaches are proposed: Signs and Uncoded methods. In Signs method, the local machines quantize their data into binary vectors and an optimal channel coding scheme is used to reliably send the vectors to the central machine where the structure is learned from the received data. In Uncoded method, data symbols are scaled and transmitted through the channel. The central machine uses the received noisy symbols to recover the structure. Theoretical results show that both methods can recover the structure with high probability for large enough sample size. Experimental results indicate the superiority of Signs method over Uncoded method under several circumstances.

Learning of Tree-Structured Gaussian Graphical Models on Distributed Data under Communication Constraints

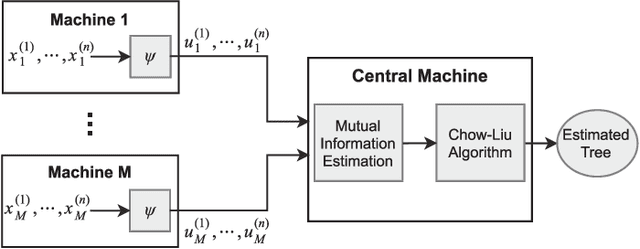
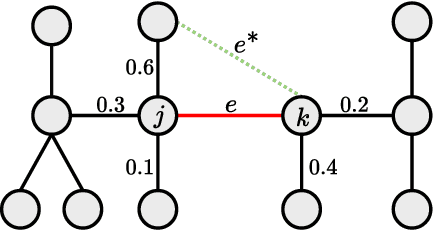
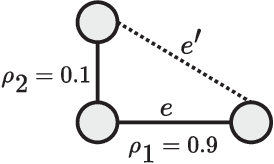
In this paper, learning of tree-structured Gaussian graphical models from distributed data is addressed. In our model, samples are stored in a set of distributed machines where each machine has access to only a subset of features. A central machine is then responsible for learning the structure based on received messages from the other nodes. We present a set of communication efficient strategies, which are theoretically proved to convey sufficient information for reliable learning of the structure. In particular, our analyses show that even if each machine sends only the signs of its local data samples to the central node, the tree structure can still be recovered with high accuracy. Our simulation results on both synthetic and real-world datasets show that our strategies achieve a desired accuracy in inferring the underlying structure, while spending a small budget on communication.

Cell Identity Codes: Understanding Cell Identity from Gene Expression Profiles using Deep Neural Networks

Understanding cell identity is an important task in many biomedical areas. Expression patterns of specific marker genes have been used to characterize some limited cell types, but exclusive markers are not available for many cell types. A second approach is to use machine learning to discriminate cell types based on the whole gene expression profiles (GEPs). The accuracies of simple classification algorithms such as linear discriminators or support vector machines are limited due to the complexity of biological systems. We used deep neural networks to analyze 1040 GEPs from 16 different human tissues and cell types. After comparing different architectures, we identified a specific structure of deep autoencoders that can encode a GEP into a vector of 30 numeric values, which we call the cell identity code (CIC). The original GEP can be reproduced from the CIC with an accuracy comparable to technical replicates of the same experiment. Although we use an unsupervised approach to train the autoencoder, we show different values of the CIC are connected to different biological aspects of the cell, such as different pathways or biological processes. This network can use CIC to reproduce the GEP of the cell types it has never seen during the training. It also can resist some noise in the measurement of the GEP. Furthermore, we introduce classifier autoencoder, an architecture that can accurately identify cell type based on the GEP or the CIC.

Learning of Gaussian Processes in Distributed and Communication Limited Systems

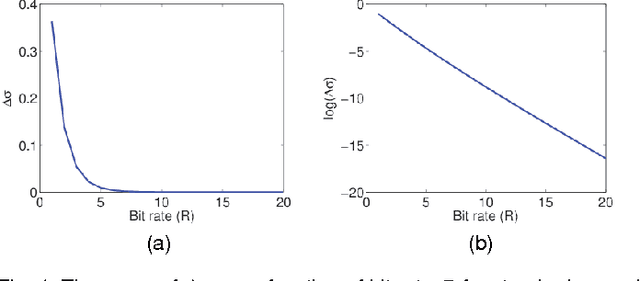
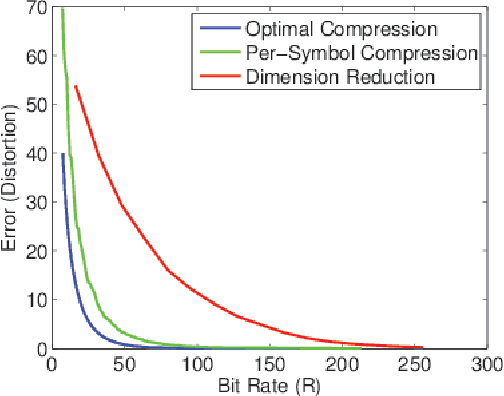
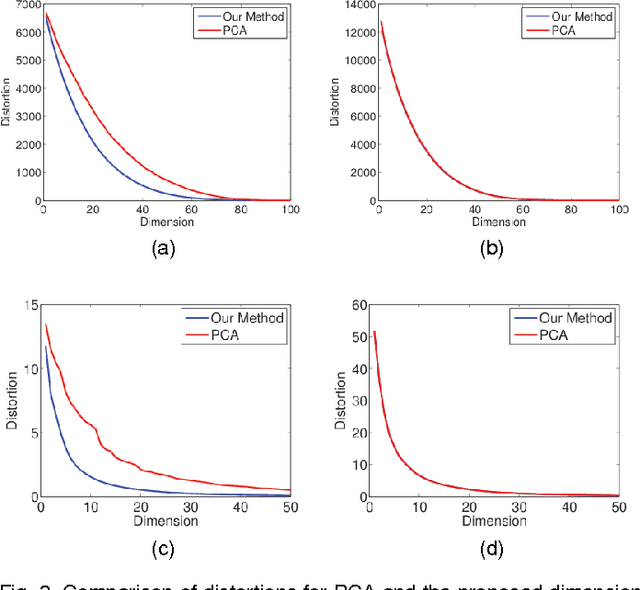
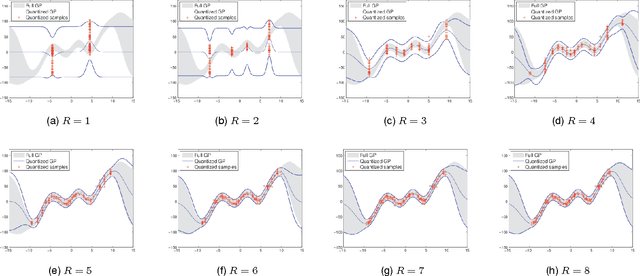
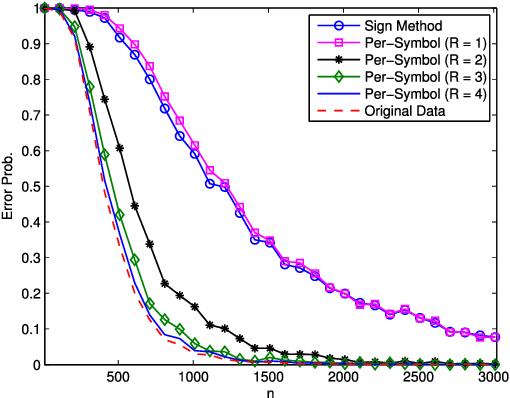
It is of fundamental importance to find algorithms obtaining optimal performance for learning of statistical models in distributed and communication limited systems. Aiming at characterizing the optimal strategies, we consider learning of Gaussian Processes (GPs) in distributed systems as a pivotal example. We first address a very basic problem: how many bits are required to estimate the inner-products of Gaussian vectors across distributed machines? Using information theoretic bounds, we obtain an optimal solution for the problem which is based on vector quantization. Two suboptimal and more practical schemes are also presented as substitute for the vector quantization scheme. In particular, it is shown that the performance of one of the practical schemes which is called per-symbol quantization is very close to the optimal one. Schemes provided for the inner-product calculations are incorporated into our proposed distributed learning methods for GPs. Experimental results show that with spending few bits per symbol in our communication scheme, our proposed methods outperform previous zero rate distributed GP learning schemes such as Bayesian Committee Model (BCM) and Product of experts (PoE).