Robust Model Evaluation over Large-scale Federated Networks

In this paper, we address the challenge of certifying the performance of a machine learning model on an unseen target network, using measurements from an available source network. We focus on a scenario where heterogeneous datasets are distributed across a source network of clients, all connected to a central server. Specifically, consider a source network "A" composed of $K$ clients, each holding private data from unique and heterogeneous distributions, which are assumed to be independent samples from a broader meta-distribution $\mu$. Our goal is to provide certified guarantees for the model's performance on a different, unseen target network "B," governed by another meta-distribution $\mu'$, assuming the deviation between $\mu$ and $\mu'$ is bounded by either the Wasserstein distance or an $f$-divergence. We derive theoretical guarantees for the model's empirical average loss and provide uniform bounds on the risk CDF, where the latter correspond to novel and adversarially robust versions of the Glivenko-Cantelli theorem and the Dvoretzky-Kiefer-Wolfowitz (DKW) inequality. Our bounds are computable in polynomial time with a polynomial number of queries to the $K$ clients, preserving client privacy by querying only the model's (potentially adversarial) loss on private data. We also establish non-asymptotic generalization bounds that consistently converge to zero as both $K$ and the minimum client sample size grow. Extensive empirical evaluations validate the robustness and practicality of our bounds across real-world tasks.

Gradual Domain Adaptation via Manifold-Constrained Distributionally Robust Optimization

The aim of this paper is to address the challenge of gradual domain adaptation within a class of manifold-constrained data distributions. In particular, we consider a sequence of $T\ge2$ data distributions $P_1,\ldots,P_T$ undergoing a gradual shift, where each pair of consecutive measures $P_i,P_{i+1}$ are close to each other in Wasserstein distance. We have a supervised dataset of size $n$ sampled from $P_0$, while for the subsequent distributions in the sequence, only unlabeled i.i.d. samples are available. Moreover, we assume that all distributions exhibit a known favorable attribute, such as (but not limited to) having intra-class soft/hard margins. In this context, we propose a methodology rooted in Distributionally Robust Optimization (DRO) with an adaptive Wasserstein radius. We theoretically show that this method guarantees the classification error across all $P_i$s can be suitably bounded. Our bounds rely on a newly introduced {\it {compatibility}} measure, which fully characterizes the error propagation dynamics along the sequence. Specifically, for inadequately constrained distributions, the error can exponentially escalate as we progress through the gradual shifts. Conversely, for appropriately constrained distributions, the error can be demonstrated to be linear or even entirely eradicated. We have substantiated our theoretical findings through several experimental results.

Unlabeled Out-Of-Domain Data Improves Generalization

We propose a novel framework for incorporating unlabeled data into semi-supervised classification problems, where scenarios involving the minimization of either i) adversarially robust or ii) non-robust loss functions have been considered. Notably, we allow the unlabeled samples to deviate slightly (in total variation sense) from the in-domain distribution. The core idea behind our framework is to combine Distributionally Robust Optimization (DRO) with self-supervised training. As a result, we also leverage efficient polynomial-time algorithms for the training stage. From a theoretical standpoint, we apply our framework on the classification problem of a mixture of two Gaussians in $\mathbb{R}^d$, where in addition to the $m$ independent and labeled samples from the true distribution, a set of $n$ (usually with $n\gg m$) out of domain and unlabeled samples are gievn as well. Using only the labeled data, it is known that the generalization error can be bounded by $\propto\left(d/m\right)^{1/2}$. However, using our method on both isotropic and non-isotropic Gaussian mixture models, one can derive a new set of analytically explicit and non-asymptotic bounds which show substantial improvement on the generalization error compared ERM. Our results underscore two significant insights: 1) out-of-domain samples, even when unlabeled, can be harnessed to narrow the generalization gap, provided that the true data distribution adheres to a form of the "cluster assumption", and 2) the semi-supervised learning paradigm can be regarded as a special case of our framework when there are no distributional shifts. We validate our claims through experiments conducted on a variety of synthetic and real-world datasets.

Sample Complexity Bounds for Learning High-dimensional Simplices in Noisy Regimes

In this paper, we propose a sample complexity bound for learning a simplex from noisy samples. A dataset of size $n$ is given which includes i.i.d. samples drawn from a uniform distribution over an unknown arbitrary simplex in $\mathbb{R}^K$, where samples are assumed to be corrupted by an additive Gaussian noise of an arbitrary magnitude. We propose a strategy which outputs a simplex having, with high probability, a total variation distance of $\epsilon + O\left(\mathrm{SNR}^{-1}\right)$ from the true simplex, for any $\epsilon>0$. We prove that to arrive this close to the true simplex, it is sufficient to have $n\ge\tilde{O}\left(K^2/\epsilon^2\right)$ samples. Here, SNR stands for the signal-to-noise ratio which can be viewed as the ratio of the diameter of the simplex to the standard deviation of the noise. Our proofs are based on recent advancements in sample compression techniques, which have already shown promises in deriving tight bounds for density estimation in high-dimensional Gaussian mixture models.

Distributed Sparse Feature Selection in Communication-Restricted Networks

This paper aims to propose and theoretically analyze a new distributed scheme for sparse linear regression and feature selection. The primary goal is to learn the few causal features of a high-dimensional dataset based on noisy observations from an unknown sparse linear model. However, the presumed training set which includes $n$ data samples in $\mathbb{R}^p$ is already distributed over a large network with $N$ clients connected through extremely low-bandwidth links. Also, we consider the asymptotic configuration of $1\ll N\ll n\ll p$. In order to infer the causal dimensions from the whole dataset, we propose a simple, yet effective method for information sharing in the network. In this regard, we theoretically show that the true causal features can be reliably recovered with negligible bandwidth usage of $O\left(N\log p\right)$ across the network. This yields a significantly lower communication cost in comparison with the trivial case of transmitting all the samples to a single node (centralized scenario), which requires $O\left(np\right)$ transmissions. Even more sophisticated schemes such as ADMM still have a communication complexity of $O\left(Np\right)$. Surprisingly, our sample complexity bound is proved to be the same (up to a constant factor) as the optimal centralized approach for a fixed performance measure in each node, while that of a na\"{i}ve decentralized technique grows linearly with $N$. Theoretical guarantees in this paper are based on the recent analytic framework of debiased LASSO in Javanmard et al. (2019), and are supported by several computer experiments performed on both synthetic and real-world datasets.

Regularizing Recurrent Neural Networks via Sequence Mixup

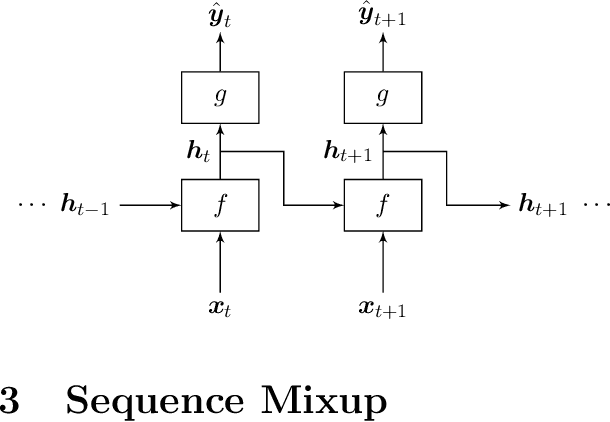
In this paper, we extend a class of celebrated regularization techniques originally proposed for feed-forward neural networks, namely Input Mixup (Zhang et al., 2017) and Manifold Mixup (Verma et al., 2018), to the realm of Recurrent Neural Networks (RNN). Our proposed methods are easy to implement and have a low computational complexity, while leverage the performance of simple neural architectures in a variety of tasks. We have validated our claims through several experiments on real-world datasets, and also provide an asymptotic theoretical analysis to further investigate the properties and potential impacts of our proposed techniques. Applying sequence mixup to BiLSTM-CRF model (Huang et al., 2015) to Named Entity Recognition task on CoNLL-2003 data (Sang and De Meulder, 2003) has improved the F-1 score on the test stage and reduced the loss, considerably.

Robustness to Adversarial Perturbations in Learning from Incomplete Data

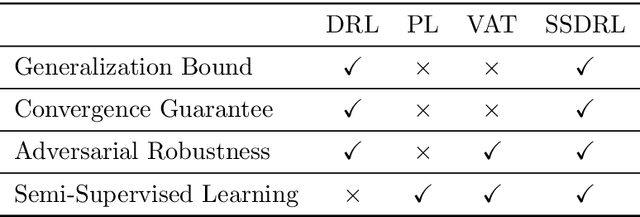
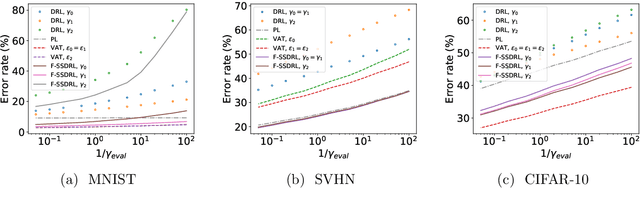
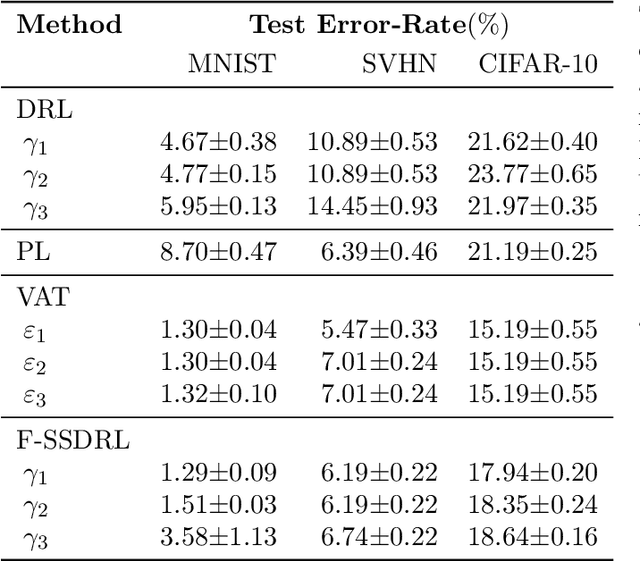
What is the role of unlabeled data in an inference problem, when the presumed underlying distribution is adversarially perturbed? To provide a concrete answer to this question, this paper unifies two major learning frameworks: Semi-Supervised Learning (SSL) and Distributionally Robust Learning (DRL). We develop a generalization theory for our framework based on a number of novel complexity measures, such as an adversarial extension of Rademacher complexity and its semi-supervised analogue. Moreover, our analysis is able to quantify the role of unlabeled data in the generalization under a more general condition compared to the existing theoretical works in SSL. Based on our framework, we also present a hybrid of DRL and EM algorithms that has a guaranteed convergence rate. When implemented with deep neural networks, our method shows a comparable performance to those of the state-of-the-art on a number of real-world benchmark datasets.

On Statistical Learning of Simplices: Unmixing Problem Revisited

Learning of high-dimensional simplices from uniformly-sampled observations, generally known as the "unmixing problem", is a long-studied task in computer science. More recently, a significant interest is focused on this problem from other areas, such as computational biology and remote sensing. In this paper, we have studied the Probably Approximately Correct (PAC)-learnability of simplices with a focus on sample complexity. Our analysis shows that a sufficient sample size for PAC-learning of $K$-simplices is only $O\left(K^2\log K\right)$, yielding a huge improvement over the existing results, i.e. $O\left(K^{22}\right)$. Moreover, a novel continuously-relaxed optimization scheme is proposed which is guaranteed to achieve a PAC-approximation of the simplex, followed by a corresponding scalable algorithm whose performance is extensively tested on synthetic and real-world datasets. Experimental results show that not only being comparable to other existing strategies on noiseless samples, our method is superior to the state-of-the-art in noisy cases. The overall proposed framework is backed with solid theoretical guarantees and provides a rigorous framework for future research in this area.

Manifold Mixup: Learning Better Representations by Interpolating Hidden States

Deep networks often perform well on the data distribution on which they are trained, yet give incorrect (and often very confident) answers when evaluated on points from off of the training distribution. This is exemplified by the adversarial examples phenomenon but can also be seen in terms of model generalization and domain shift. Ideally, a model would assign lower confidence to points unlike those from the training distribution. We propose a regularizer which addresses this issue by training with interpolated hidden states and encouraging the classifier to be less confident at these points. Because the hidden states are learned, this has an important effect of encouraging the hidden states for a class to be concentrated in such a way so that interpolations within the same class or between two different classes do not intersect with the real data points from other classes. This has a major advantage in that it avoids the underfitting which can result from interpolating in the input space. We prove that the exact condition for this problem of underfitting to be avoided by Manifold Mixup is that the dimensionality of the hidden states exceeds the number of classes, which is often the case in practice. Additionally, this concentration can be seen as making the features in earlier layers more discriminative. We show that despite requiring no significant additional computation, Manifold Mixup achieves large improvements over strong baselines in supervised learning, robustness to single-step adversarial attacks, semi-supervised learning, and Negative Log-Likelihood on held out samples.

Reliable Learning of Bernoulli Mixture Models

In this paper, we have derived a set of sufficient conditions for reliable clustering of data produced by Bernoulli Mixture Models (BMM), when the number of clusters is unknown. A BMM refers to a random binary vector whose components are independent Bernoulli trials with cluster-specific frequencies. The problem of clustering BMM data arises in many real-world applications, most notably in population genetics where researchers aim at inferring the population structure from multilocus genotype data. Our findings stipulate a minimum dataset size and a minimum number of Bernoulli trials (or genotyped loci) per sample, such that the existence of a clustering algorithm with a sufficient accuracy is guaranteed. Moreover, the mathematical intuitions and tools behind our work can help researchers in designing more effective and theoretically-plausible heuristic methods for similar problems.