Scalable Nonlinear AUC Maximization Methods

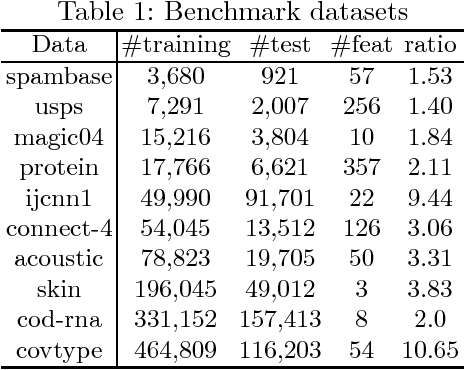
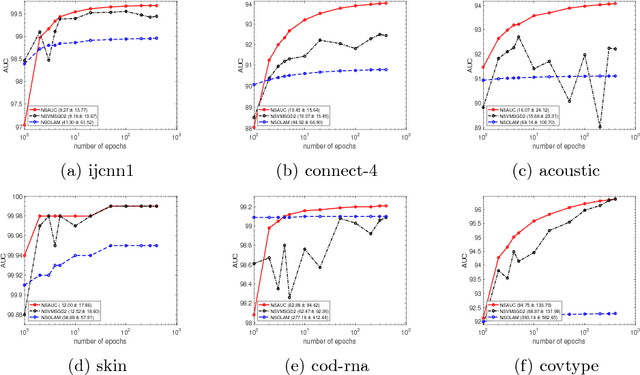
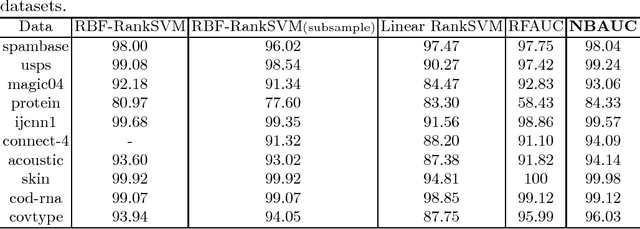
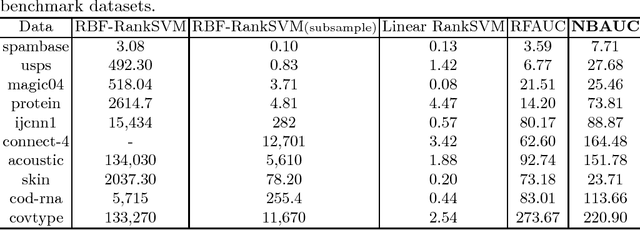
The area under the ROC curve (AUC) is a measure of interest in various machine learning and data mining applications. It has been widely used to evaluate classification performance on heavily imbalanced data. The kernelized AUC maximization machines have established a superior generalization ability compared to linear AUC machines because of their capability in modeling the complex nonlinear structure underlying most real-world data. However, the high training complexity renders the kernelized AUC machines infeasible for large-scale data. In this paper, we present two nonlinear AUC maximization algorithms that optimize pairwise linear classifiers over a finite-dimensional feature space constructed via the k-means Nystr\"{o}m method. Our first algorithm maximize the AUC metric by optimizing a pairwise squared hinge loss function using the truncated Newton method. However, the second-order batch AUC maximization method becomes expensive to optimize for extremely massive datasets. This motivate us to develop a first-order stochastic AUC maximization algorithm that incorporates a scheduled regularization update and scheduled averaging techniques to accelerate the convergence of the classifier. Experiments on several benchmark datasets demonstrate that the proposed AUC classifiers are more efficient than kernelized AUC machines while they are able to surpass or at least match the AUC performance of the kernelized AUC machines. The experiments also show that the proposed stochastic AUC classifier outperforms the state-of-the-art online AUC maximization methods in terms of AUC classification accuracy.

Inferring Molecular Pathology and micro-RNA Transcriptome from mRNA Profiles of Cancer Biopsies through Deep Multi-Task Learning

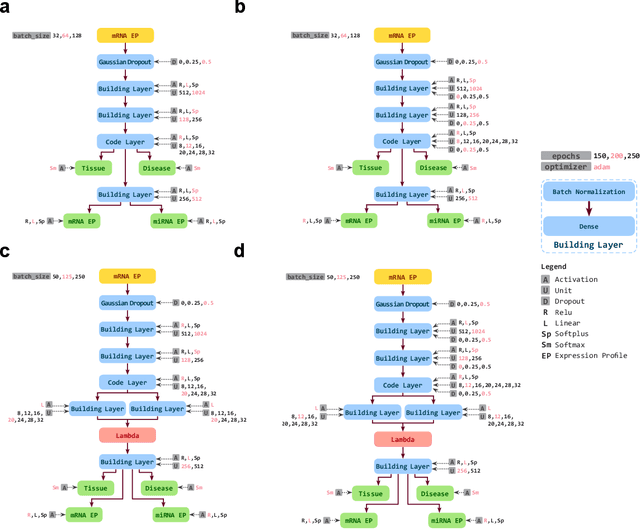
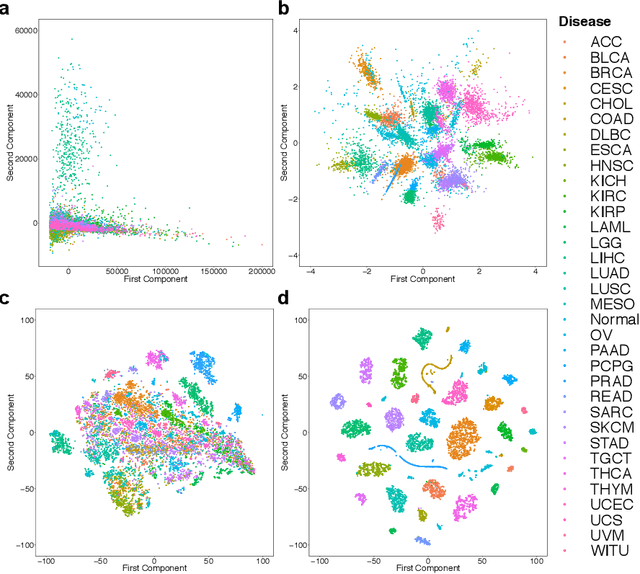
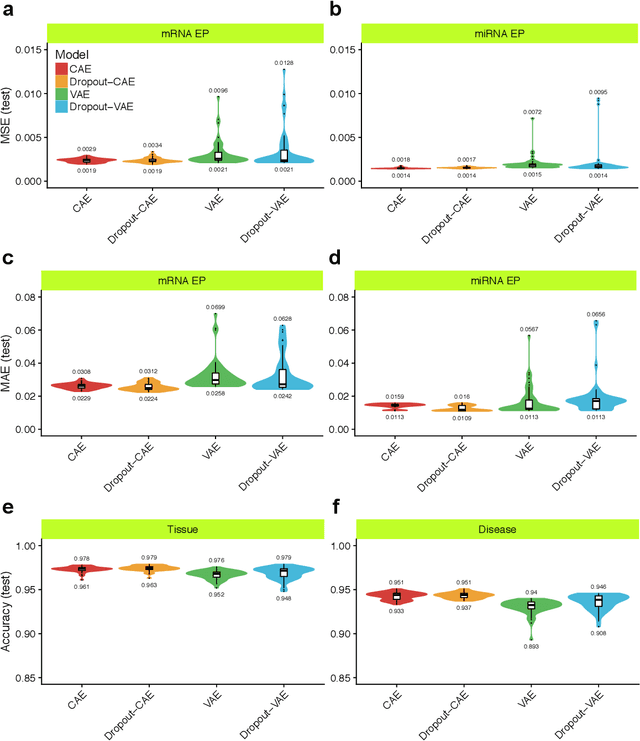
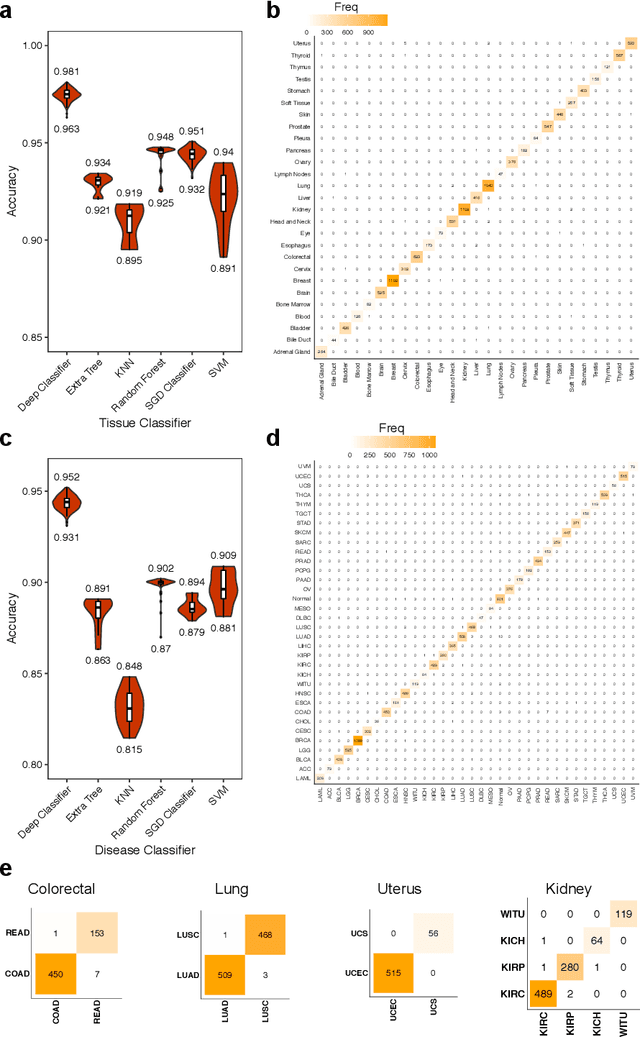
Despite great advances, molecular cancer pathology is often limited to use a small number of biomarkers rather than the whole transcriptome, partly due to the computational challenges. Here, we introduce a novel architecture of DNNs that is capable of simultaneous inference of various properties of biological samples, through multi-task and transfer learning. We employed this architecture on mRNA transcription profiles of 10787 clinical samples from 34 classes (one healthy and 33 different types of cancer) from 27 tissues. Our system significantly outperforms prior works and classical machine learning approaches in predicting tissue-of-origin, normal or disease state and cancer type of each sample. Furthermore, it can predict miRNA transcription profile of each sample, which enables performing miRNA expression research when only mRNA transcriptome data are available. We also show this system is very robust against noise and missing values. Collectively, our results highlight applications of artificial intelligence in molecular cancer pathology and oncological research.

Cell Identity Codes: Understanding Cell Identity from Gene Expression Profiles using Deep Neural Networks

Understanding cell identity is an important task in many biomedical areas. Expression patterns of specific marker genes have been used to characterize some limited cell types, but exclusive markers are not available for many cell types. A second approach is to use machine learning to discriminate cell types based on the whole gene expression profiles (GEPs). The accuracies of simple classification algorithms such as linear discriminators or support vector machines are limited due to the complexity of biological systems. We used deep neural networks to analyze 1040 GEPs from 16 different human tissues and cell types. After comparing different architectures, we identified a specific structure of deep autoencoders that can encode a GEP into a vector of 30 numeric values, which we call the cell identity code (CIC). The original GEP can be reproduced from the CIC with an accuracy comparable to technical replicates of the same experiment. Although we use an unsupervised approach to train the autoencoder, we show different values of the CIC are connected to different biological aspects of the cell, such as different pathways or biological processes. This network can use CIC to reproduce the GEP of the cell types it has never seen during the training. It also can resist some noise in the measurement of the GEP. Furthermore, we introduce classifier autoencoder, an architecture that can accurately identify cell type based on the GEP or the CIC.

Confidence-Weighted Bipartite Ranking

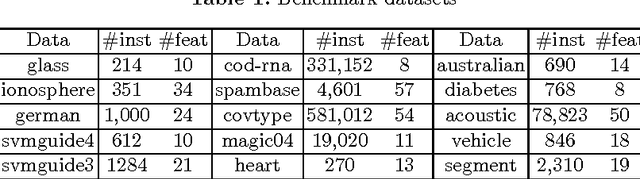
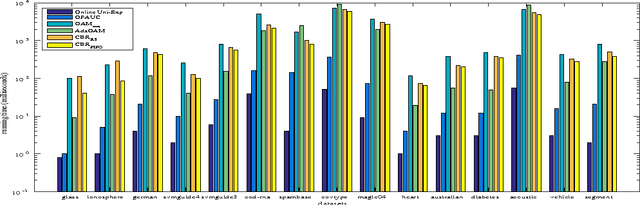
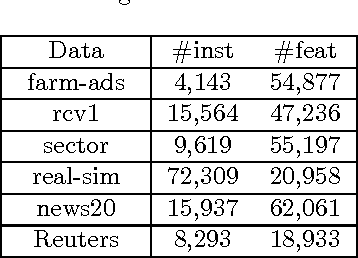
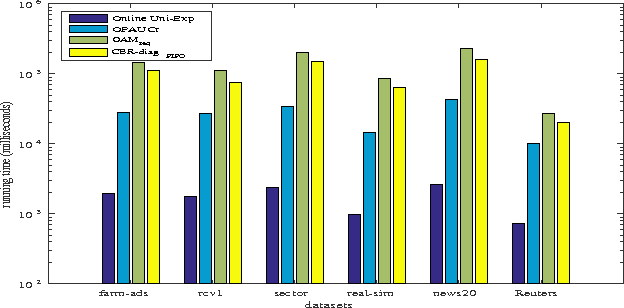
Bipartite ranking is a fundamental machine learning and data mining problem. It commonly concerns the maximization of the AUC metric. Recently, a number of studies have proposed online bipartite ranking algorithms to learn from massive streams of class-imbalanced data. These methods suggest both linear and kernel-based bipartite rank- ing algorithms based on first and second-order online learning. Unlike kernelized ranker, linear ranker is more scalable learning algorithm. The existing linear online bipartite ranking algorithms lack either handling non-separable data or constructing adaptive large margin. These limitations yield unreliable bipartite ranking performance. In this work, we propose a linear online confidence-weighted bipartite ranking algorithm (CBR) that adopts soft confidence-weighted learning. The proposed algorithm leverages the same properties of soft confidence-weighted learning in a framework for bipartite ranking. We also develop a diagonal variation of the proposed confidence-weighted bipartite ranking algorithm to deal with high-dimensional data by maintaining only the diagonal elements of the covariance matrix. We empirically evaluate the effectiveness of the proposed algorithms on several benchmark and high-dimensional datasets. The experimental results validate the reliability of the pro- posed algorithms. The results also show that our algorithms outperform or are at least comparable to the competing online AUC maximization methods.

Proceedings of the 1st International Workshop on Robot Learning and Planning

Proceedings of the 1st International Workshop on Robot Learning and Planning (RLP 2016)

NUROA: A Numerical Roadmap Algorithm

Motion planning has been studied for nearly four decades now. Complete, combinatorial motion planning approaches are theoretically well-rooted with completeness guarantees but they are hard to implement. Sampling-based and heuristic methods are easy to implement and quite simple to customize but they lack completeness guarantees. Can the best of both worlds be ever achieved, particularly for mission critical applications such as robotic surgery, space explorations, and handling hazardous material? In this paper, we answer affirmatively to that question. We present a new methodology, NUROA, to numerically approximate the Canny's roadmap, which is a network of one-dimensional algebraic curves. Our algorithm encloses the roadmap with a chain of tiny boxes each of which contains a piece of the roadmap and whose connectivity captures the roadmap connectivity. It starts by enclosing the entire space with a box. In each iteration, remaining boxes are shrunk on all sides and then split into smaller sized boxes. Those boxes that are empty are detected in the shrink phase and removed. The algorithm terminates when all remaining boxes are smaller than a resolution that can be either given as input or automatically computed using root separation lower bounds. Shrink operation is cast as a polynomial optimization with semialgebraic constraints, which is in turn transformed into a (series of) semidefinite programs (SDP) using the Lasserre's approach. NUROA's success is due to fast SDP solvers. NUROA correctly captured the connectivity of multiple curves/skeletons whereas competitors such as IBEX and Realpaver failed in some cases. Since boxes are independent from one another, NUROA can be parallelized particularly on GPUs. NUROA is available as an open source package at http://nuroa.sourceforge.net/.

Proceedings of the 1st Workshop on Robotics Challenges and Vision

Proceedings of the 1st Workshop on Robotics Challenges and Vision (RCV2013)

Exact Learning of RNA Energy Parameters From Structure

We consider the problem of exact learning of parameters of a linear RNA energy model from secondary structure data. A necessary and sufficient condition for learnability of parameters is derived, which is based on computing the convex hull of union of translated Newton polytopes of input sequences. The set of learned energy parameters is characterized as the convex cone generated by the normal vectors to those facets of the resulting polytope that are incident to the origin. In practice, the sufficient condition may not be satisfied by the entire training data set; hence, computing a maximal subset of training data for which the sufficient condition is satisfied is often desired. We show that problem is NP-hard in general for an arbitrary dimensional feature space. Using a randomized greedy algorithm, we select a subset of RNA STRAND v2.0 database that satisfies the sufficient condition for separate A-U, C-G, G-U base pair counting model. The set of learned energy parameters includes experimentally measured energies of A-U, C-G, and G-U pairs; hence, our parameter set is in agreement with the Turner parameters.

On Time-optimal Trajectories for a Car-like Robot with One Trailer

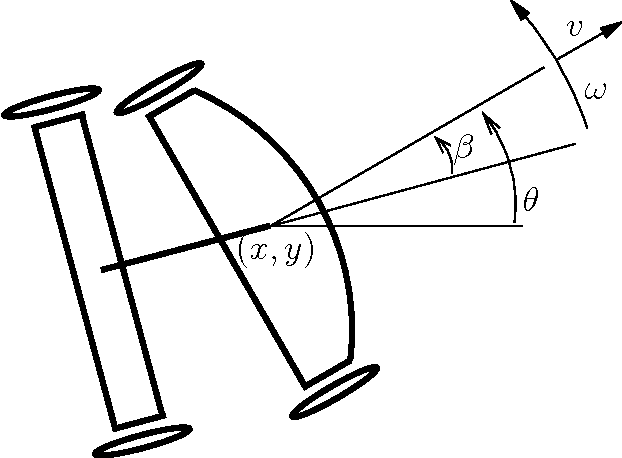
In addition to the theoretical value of challenging optimal control problmes, recent progress in autonomous vehicles mandates further research in optimal motion planning for wheeled vehicles. Since current numerical optimal control techniques suffer from either the curse of dimens ionality, e.g. the Hamilton-Jacobi-Bellman equation, or the curse of complexity, e.g. pseudospectral optimal control and max-plus methods, analytical characterization of geodesics for wheeled vehicles becomes important not only from a theoretical point of view but also from a prac tical one. Such an analytical characterization provides a fast motion planning algorithm that can be used in robust feedback loops. In this work, we use the Pontryagin Maximum Principle to characterize extremal trajectories, i.e. candidate geodesics, for a car-like robot with one trailer. We use time as the distance function. In spite of partial progress, this problem has remained open in the past two decades. Besides straight motion and turn with maximum allowed curvature, we identify planar elastica as the third piece of motion that occurs along our extr emals. We give a detailed characterization of such curves, a special case of which, called \emph{merging curve}, connects maximum curvature turns to straight line segments. The structure of extremals in our case is revealed through analytical integration of the system and adjoint equations.

The RNA Newton Polytope and Learnability of Energy Parameters

Despite nearly two scores of research on RNA secondary structure and RNA-RNA interaction prediction, the accuracy of the state-of-the-art algorithms are still far from satisfactory. Researchers have proposed increasingly complex energy models and improved parameter estimation methods in anticipation of endowing their methods with enough power to solve the problem. The output has disappointingly been only modest improvements, not matching the expectations. Even recent massively featured machine learning approaches were not able to break the barrier. In this paper, we introduce the notion of learnability of the parameters of an energy model as a measure of its inherent capability. We say that the parameters of an energy model are learnable iff there exists at least one set of such parameters that renders every known RNA structure to date the minimum free energy structure. We derive a necessary condition for the learnability and give a dynamic programming algorithm to assess it. Our algorithm computes the convex hull of the feature vectors of all feasible structures in the ensemble of a given input sequence. Interestingly, that convex hull coincides with the Newton polytope of the partition function as a polynomial in energy parameters. We demonstrated the application of our theory to a simple energy model consisting of a weighted count of A-U and C-G base pairs. Our results show that this simple energy model satisfies the necessary condition for less than one third of the input unpseudoknotted sequence-structure pairs chosen from the RNA STRAND v2.0 database. For another one third, the necessary condition is barely violated, which suggests that augmenting this simple energy model with more features such as the Turner loops may solve the problem. The necessary condition is severely violated for 8%, which provides a small set of hard cases that require further investigation.