Scalable Nonlinear AUC Maximization Methods

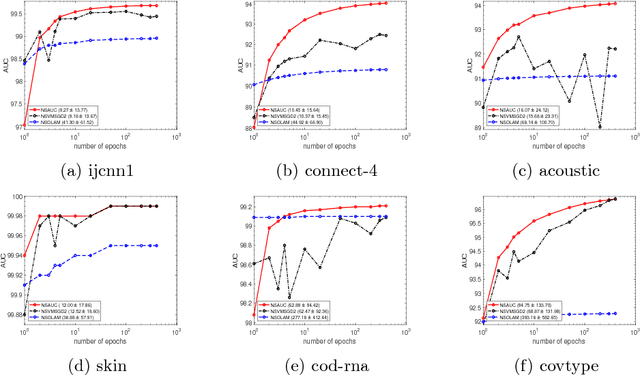
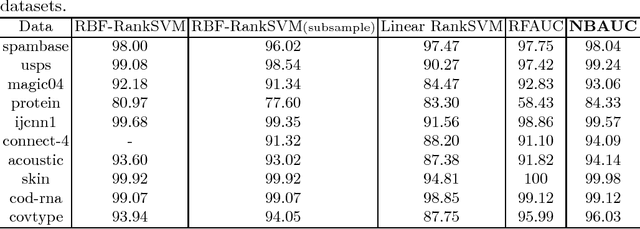
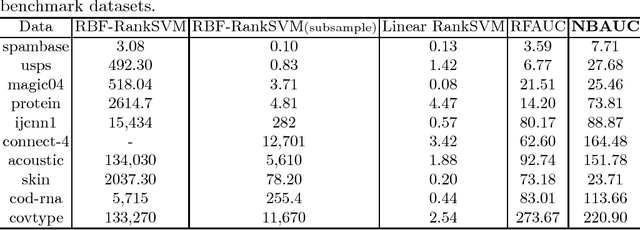
The area under the ROC curve (AUC) is a measure of interest in various machine learning and data mining applications. It has been widely used to evaluate classification performance on heavily imbalanced data. The kernelized AUC maximization machines have established a superior generalization ability compared to linear AUC machines because of their capability in modeling the complex nonlinear structure underlying most real-world data. However, the high training complexity renders the kernelized AUC machines infeasible for large-scale data. In this paper, we present two nonlinear AUC maximization algorithms that optimize pairwise linear classifiers over a finite-dimensional feature space constructed via the k-means Nystr\"{o}m method. Our first algorithm maximize the AUC metric by optimizing a pairwise squared hinge loss function using the truncated Newton method. However, the second-order batch AUC maximization method becomes expensive to optimize for extremely massive datasets. This motivate us to develop a first-order stochastic AUC maximization algorithm that incorporates a scheduled regularization update and scheduled averaging techniques to accelerate the convergence of the classifier. Experiments on several benchmark datasets demonstrate that the proposed AUC classifiers are more efficient than kernelized AUC machines while they are able to surpass or at least match the AUC performance of the kernelized AUC machines. The experiments also show that the proposed stochastic AUC classifier outperforms the state-of-the-art online AUC maximization methods in terms of AUC classification accuracy.

Confidence-Weighted Bipartite Ranking

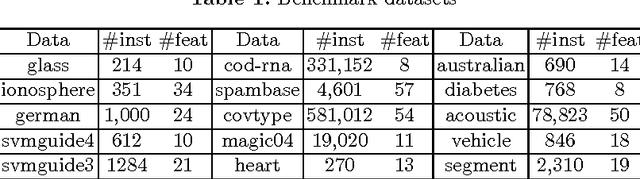
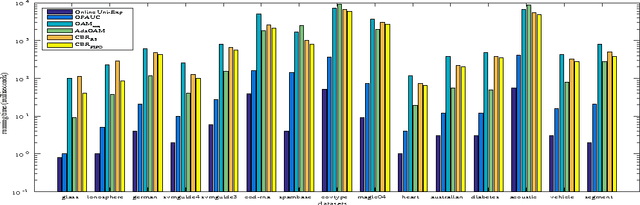
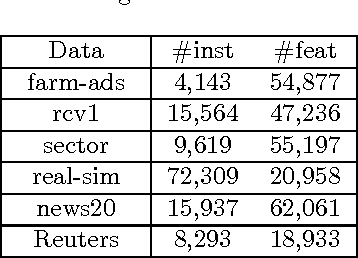
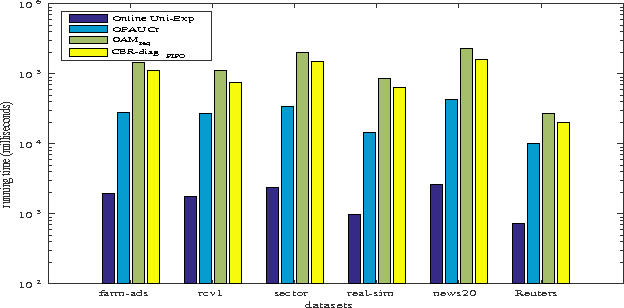
Bipartite ranking is a fundamental machine learning and data mining problem. It commonly concerns the maximization of the AUC metric. Recently, a number of studies have proposed online bipartite ranking algorithms to learn from massive streams of class-imbalanced data. These methods suggest both linear and kernel-based bipartite rank- ing algorithms based on first and second-order online learning. Unlike kernelized ranker, linear ranker is more scalable learning algorithm. The existing linear online bipartite ranking algorithms lack either handling non-separable data or constructing adaptive large margin. These limitations yield unreliable bipartite ranking performance. In this work, we propose a linear online confidence-weighted bipartite ranking algorithm (CBR) that adopts soft confidence-weighted learning. The proposed algorithm leverages the same properties of soft confidence-weighted learning in a framework for bipartite ranking. We also develop a diagonal variation of the proposed confidence-weighted bipartite ranking algorithm to deal with high-dimensional data by maintaining only the diagonal elements of the covariance matrix. We empirically evaluate the effectiveness of the proposed algorithms on several benchmark and high-dimensional datasets. The experimental results validate the reliability of the pro- posed algorithms. The results also show that our algorithms outperform or are at least comparable to the competing online AUC maximization methods.