Tiled Bit Networks: Sub-Bit Neural Network Compression Through Reuse of Learnable Binary Vectors

Binary Neural Networks (BNNs) enable efficient deep learning by saving on storage and computational costs. However, as the size of neural networks continues to grow, meeting computational requirements remains a challenge. In this work, we propose a new form of quantization to tile neural network layers with sequences of bits to achieve sub-bit compression of binary-weighted neural networks. The method learns binary vectors (i.e. tiles) to populate each layer of a model via aggregation and reshaping operations. During inference, the method reuses a single tile per layer to represent the full tensor. We employ the approach to both fully-connected and convolutional layers, which make up the breadth of space in most neural architectures. Empirically, the approach achieves near fullprecision performance on a diverse range of architectures (CNNs, Transformers, MLPs) and tasks (classification, segmentation, and time series forecasting) with up to an 8x reduction in size compared to binary-weighted models. We provide two implementations for Tiled Bit Networks: 1) we deploy the model to a microcontroller to assess its feasibility in resource-constrained environments, and 2) a GPU-compatible inference kernel to facilitate the reuse of a single tile per layer in memory.

Cross-Silo Federated Learning Across Divergent Domains with Iterative Parameter Alignment

Learning from the collective knowledge of data dispersed across private sources can provide neural networks with enhanced generalization capabilities. Federated learning, a method for collaboratively training a machine learning model across remote clients, achieves this by combining client models via the orchestration of a central server. However, current approaches face two critical limitations: i) they struggle to converge when client domains are sufficiently different, and ii) current aggregation techniques produce an identical global model for each client. In this work, we address these issues by reformulating the typical federated learning setup: rather than learning a single global model, we learn N models each optimized for a common objective. To achieve this, we apply a weighted distance minimization to model parameters shared in a peer-to-peer topology. The resulting framework, Iterative Parameter Alignment, applies naturally to the cross-silo setting, and has the following properties: (i) a unique solution for each participant, with the option to globally converge each model in the federation, and (ii) an optional early-stopping mechanism to elicit fairness among peers in collaborative learning settings. These characteristics jointly provide a flexible new framework for iteratively learning from peer models trained on disparate datasets. We find that the technique achieves competitive results on a variety of data partitions compared to state-of-the-art approaches. Further, we show that the method is robust to divergent domains (i.e. disjoint classes across peers) where existing approaches struggle.

Sparse Binary Transformers for Multivariate Time Series Modeling

Compressed Neural Networks have the potential to enable deep learning across new applications and smaller computational environments. However, understanding the range of learning tasks in which such models can succeed is not well studied. In this work, we apply sparse and binary-weighted Transformers to multivariate time series problems, showing that the lightweight models achieve accuracy comparable to that of dense floating-point Transformers of the same structure. Our model achieves favorable results across three time series learning tasks: classification, anomaly detection, and single-step forecasting. Additionally, to reduce the computational complexity of the attention mechanism, we apply two modifications, which show little to no decline in model performance: 1) in the classification task, we apply a fixed mask to the query, key, and value activations, and 2) for forecasting and anomaly detection, which rely on predicting outputs at a single point in time, we propose an attention mask to allow computation only at the current time step. Together, each compression technique and attention modification substantially reduces the number of non-zero operations necessary in the Transformer. We measure the computational savings of our approach over a range of metrics including parameter count, bit size, and floating point operation (FLOPs) count, showing up to a 53x reduction in storage size and up to 10.5x reduction in FLOPs.

Scalable Nonlinear AUC Maximization Methods

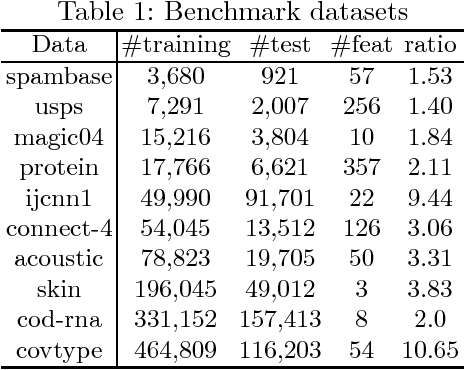
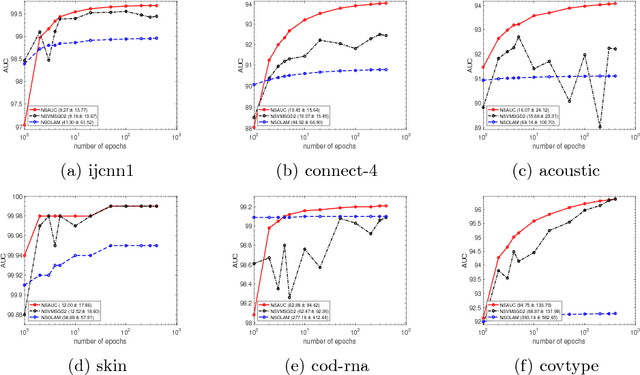
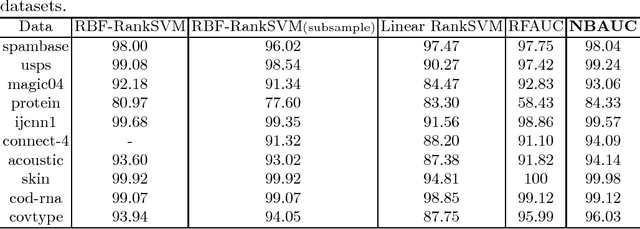
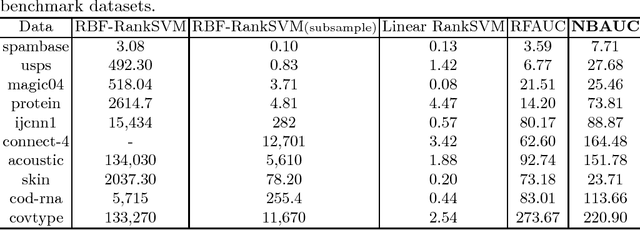
The area under the ROC curve (AUC) is a measure of interest in various machine learning and data mining applications. It has been widely used to evaluate classification performance on heavily imbalanced data. The kernelized AUC maximization machines have established a superior generalization ability compared to linear AUC machines because of their capability in modeling the complex nonlinear structure underlying most real-world data. However, the high training complexity renders the kernelized AUC machines infeasible for large-scale data. In this paper, we present two nonlinear AUC maximization algorithms that optimize pairwise linear classifiers over a finite-dimensional feature space constructed via the k-means Nystr\"{o}m method. Our first algorithm maximize the AUC metric by optimizing a pairwise squared hinge loss function using the truncated Newton method. However, the second-order batch AUC maximization method becomes expensive to optimize for extremely massive datasets. This motivate us to develop a first-order stochastic AUC maximization algorithm that incorporates a scheduled regularization update and scheduled averaging techniques to accelerate the convergence of the classifier. Experiments on several benchmark datasets demonstrate that the proposed AUC classifiers are more efficient than kernelized AUC machines while they are able to surpass or at least match the AUC performance of the kernelized AUC machines. The experiments also show that the proposed stochastic AUC classifier outperforms the state-of-the-art online AUC maximization methods in terms of AUC classification accuracy.

Confidence-Weighted Bipartite Ranking

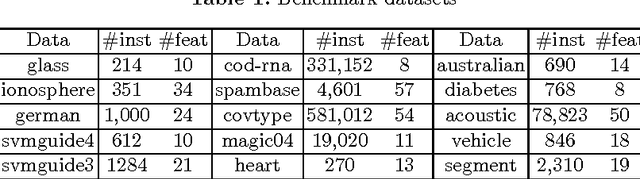
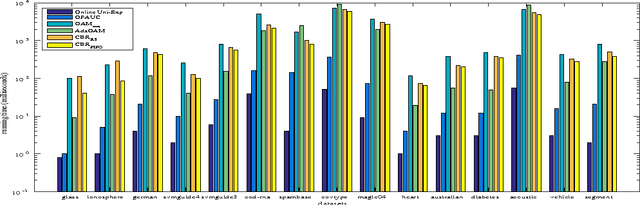
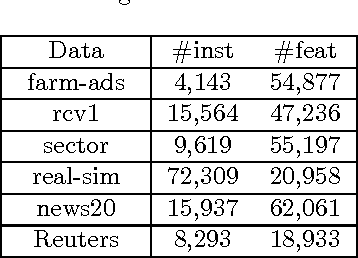
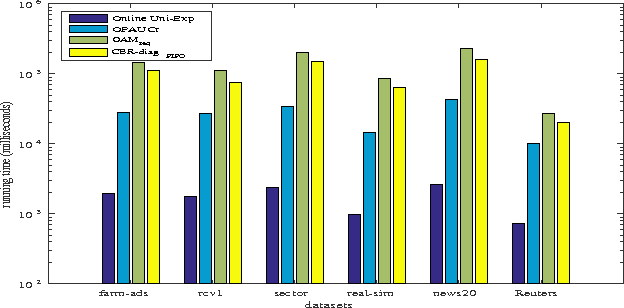
Bipartite ranking is a fundamental machine learning and data mining problem. It commonly concerns the maximization of the AUC metric. Recently, a number of studies have proposed online bipartite ranking algorithms to learn from massive streams of class-imbalanced data. These methods suggest both linear and kernel-based bipartite rank- ing algorithms based on first and second-order online learning. Unlike kernelized ranker, linear ranker is more scalable learning algorithm. The existing linear online bipartite ranking algorithms lack either handling non-separable data or constructing adaptive large margin. These limitations yield unreliable bipartite ranking performance. In this work, we propose a linear online confidence-weighted bipartite ranking algorithm (CBR) that adopts soft confidence-weighted learning. The proposed algorithm leverages the same properties of soft confidence-weighted learning in a framework for bipartite ranking. We also develop a diagonal variation of the proposed confidence-weighted bipartite ranking algorithm to deal with high-dimensional data by maintaining only the diagonal elements of the covariance matrix. We empirically evaluate the effectiveness of the proposed algorithms on several benchmark and high-dimensional datasets. The experimental results validate the reliability of the pro- posed algorithms. The results also show that our algorithms outperform or are at least comparable to the competing online AUC maximization methods.