Confidence-Weighted Bipartite Ranking

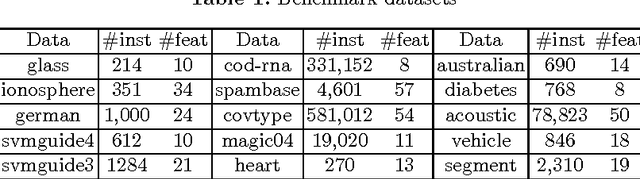
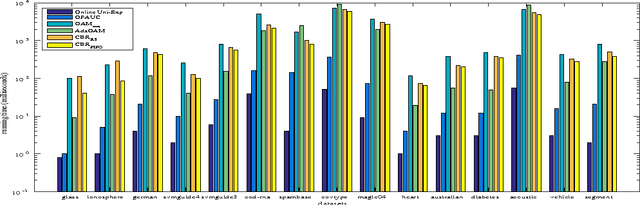
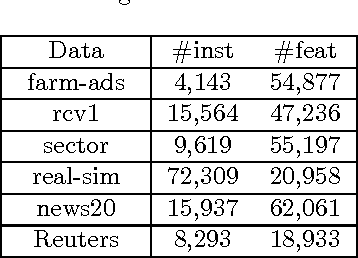
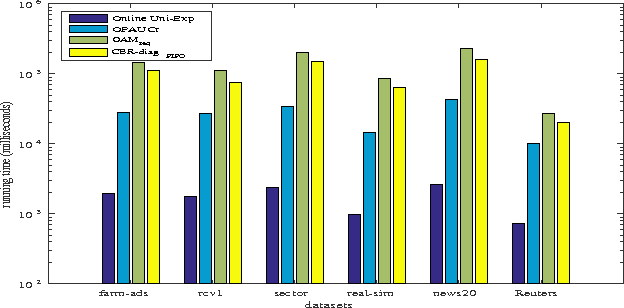
Bipartite ranking is a fundamental machine learning and data mining problem. It commonly concerns the maximization of the AUC metric. Recently, a number of studies have proposed online bipartite ranking algorithms to learn from massive streams of class-imbalanced data. These methods suggest both linear and kernel-based bipartite rank- ing algorithms based on first and second-order online learning. Unlike kernelized ranker, linear ranker is more scalable learning algorithm. The existing linear online bipartite ranking algorithms lack either handling non-separable data or constructing adaptive large margin. These limitations yield unreliable bipartite ranking performance. In this work, we propose a linear online confidence-weighted bipartite ranking algorithm (CBR) that adopts soft confidence-weighted learning. The proposed algorithm leverages the same properties of soft confidence-weighted learning in a framework for bipartite ranking. We also develop a diagonal variation of the proposed confidence-weighted bipartite ranking algorithm to deal with high-dimensional data by maintaining only the diagonal elements of the covariance matrix. We empirically evaluate the effectiveness of the proposed algorithms on several benchmark and high-dimensional datasets. The experimental results validate the reliability of the pro- posed algorithms. The results also show that our algorithms outperform or are at least comparable to the competing online AUC maximization methods.