SRViT: Vision Transformers for Estimating Radar Reflectivity from Satellite Observations at Scale

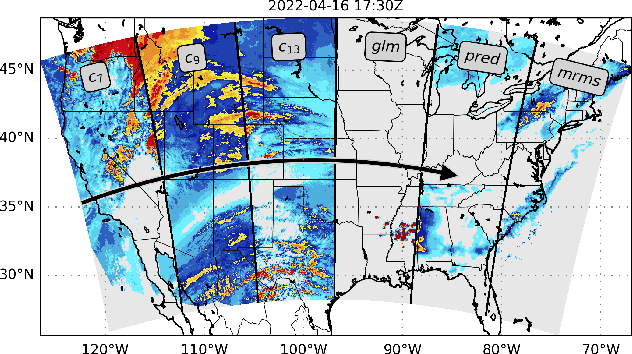
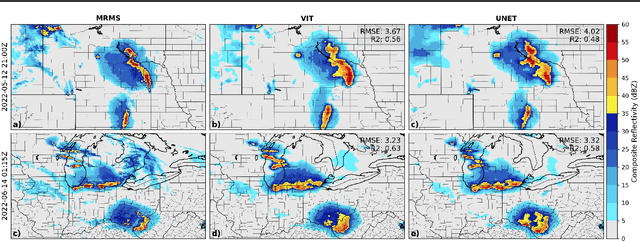
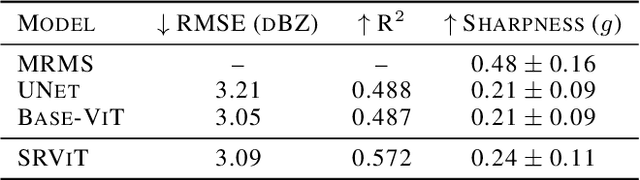
We introduce a transformer-based neural network to generate high-resolution (3km) synthetic radar reflectivity fields at scale from geostationary satellite imagery. This work aims to enhance short-term convective-scale forecasts of high-impact weather events and aid in data assimilation for numerical weather prediction over the United States. Compared to convolutional approaches, which have limited receptive fields, our results show improved sharpness and higher accuracy across various composite reflectivity thresholds. Additional case studies over specific atmospheric phenomena support our quantitative findings, while a novel attribution method is introduced to guide domain experts in understanding model outputs.

An Interpretable Model of Climate Change Using Correlative Learning

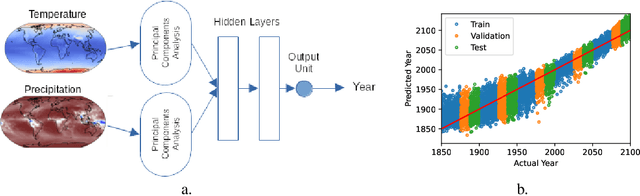
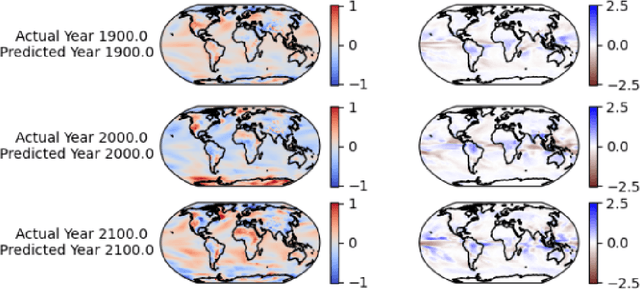
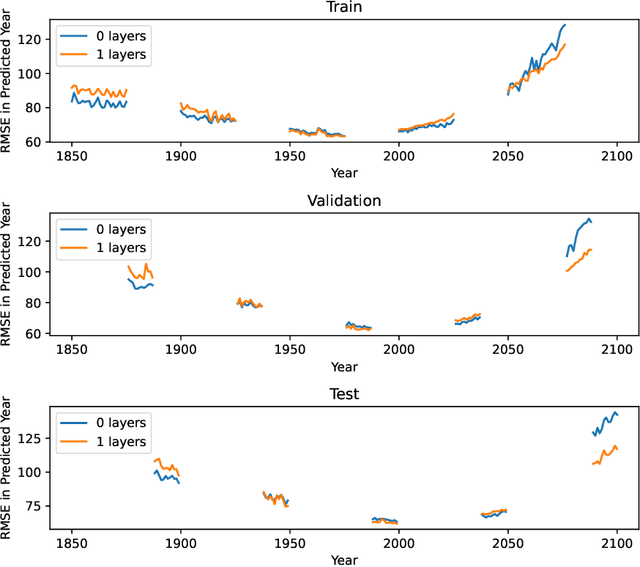
Determining changes in global temperature and precipitation that may indicate climate change is complicated by annual variations. One approach for finding potential climate change indicators is to train a model that predicts the year from annual means of global temperatures and precipitations. Such data is available from the CMIP6 ensemble of simulations. Here a two-hidden-layer neural network trained on this data successfully predicts the year. Differences among temperature and precipitation patterns for which the model predicts specific years reveal changes through time. To find these optimal patterns, a new way of interpreting what the neural network has learned is explored. Alopex, a stochastic correlative learning algorithm, is used to find optimal temperature and precipitation maps that best predict a given year. These maps are compared over multiple years to show how temperature and precipitations patterns indicative of each year change over time.

Interpretable Climate Change Modeling With Progressive Cascade Networks

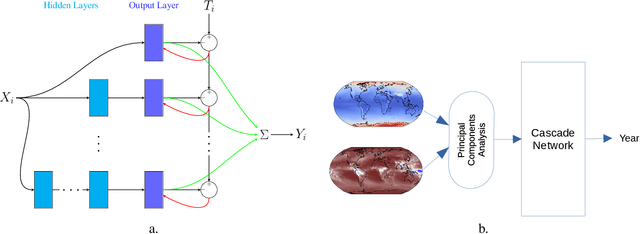
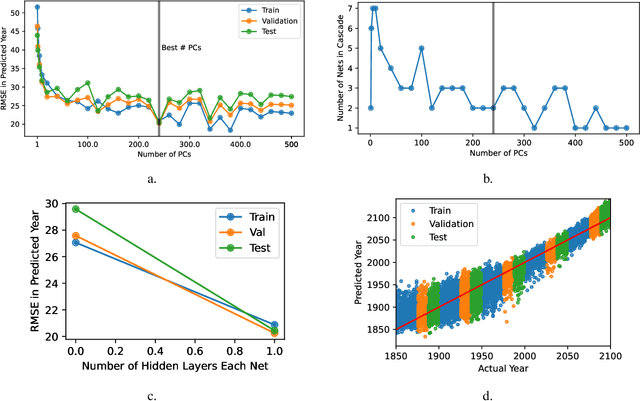
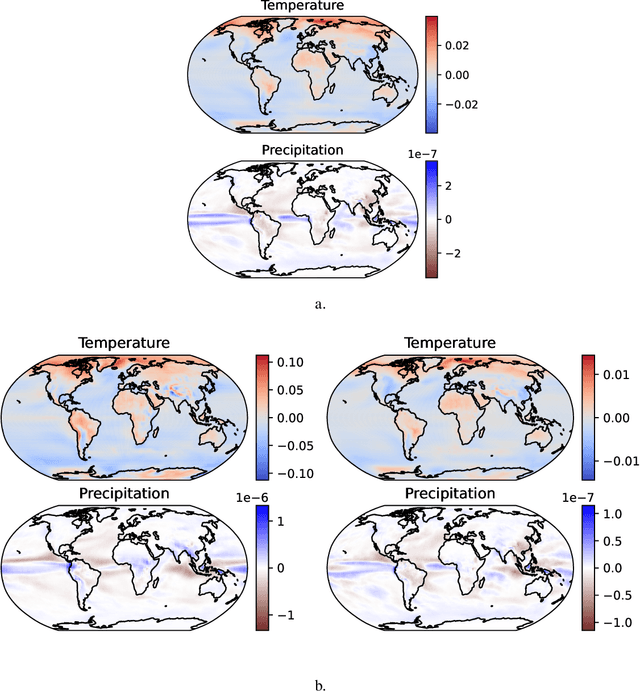
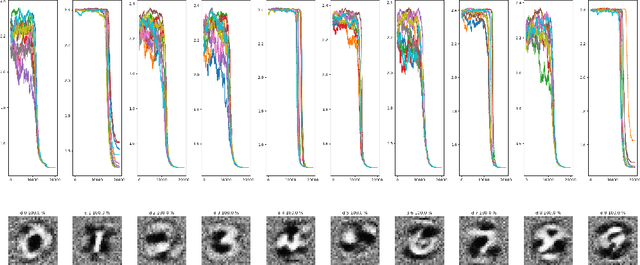
Typical deep learning approaches to modeling high-dimensional data often result in complex models that do not easily reveal a new understanding of the data. Research in the deep learning field is very actively pursuing new methods to interpret deep neural networks and to reduce their complexity. An approach is described here that starts with linear models and incrementally adds complexity only as supported by the data. An application is shown in which models that map global temperature and precipitation to years are trained to investigate patterns associated with changes in climate.

Proceedings of the 1st International Workshop on Robot Learning and Planning

Proceedings of the 1st International Workshop on Robot Learning and Planning (RLP 2016)

Optimal Nudging: Solving Average-Reward Semi-Markov Decision Processes as a Minimal Sequence of Cumulative Tasks

This paper describes a novel method to solve average-reward semi-Markov decision processes, by reducing them to a minimal sequence of cumulative reward problems. The usual solution methods for this type of problems update the gain (optimal average reward) immediately after observing the result of taking an action. The alternative introduced, optimal nudging, relies instead on setting the gain to some fixed value, which transitorily makes the problem a cumulative-reward task, solving it by any standard reinforcement learning method, and only then updating the gain in a way that minimizes uncertainty in a minmax sense. The rule for optimal gain update is derived by exploiting the geometric features of the w-l space, a simple mapping of the space of policies. The total number of cumulative reward tasks that need to be solved is shown to be small. Some experiments are presented to explore the features of the algorithm and to compare its performance with other approaches.