Probabilistic Forecasting of Localized Wildfire Spread Based on Conditional Flow Matching

This study presents a probabilistic surrogate model for localized wildfire spread based on a conditional flow matching algorithm. The approach models fire progression as a stochastic process by learning the conditional distribution of fire arrival times given the current fire state along with environmental and atmospheric inputs. Model inputs include current burned area, near-surface wind components, temperature, relative humidity, terrain height, and fuel category information, all defined on a high-resolution spatial grid. The outputs are samples of arrival time within a three-hour time window, conditioned on the input variables. Training data are generated from coupled atmosphere-wildfire spread simulations using WRF-SFIRE, paired with weather fields from the North American Mesoscale model. The proposed framework enables efficient generation of ensembles of arrival times and explicitly represents uncertainty arising from incomplete knowledge of the fire-atmosphere system and unresolved variables. The model supports localized prediction over subdomains, reducing computational cost relative to physics-based simulators while retaining sensitivity to key drivers of fire spread. Model performance is evaluated against WRF-SFIRE simulations for both single-step (3-hour) and recursive multi-step (24-hour) forecasts. Results demonstrate that the method captures variability in fire evolution and produces accurate ensemble predictions. The framework provides a scalable approach for probabilistic wildfire forecasting and offers a pathway for integrating machine learning models with operational fire prediction systems and data assimilation.

Generative Algorithms for Wildfire Progression Reconstruction from Multi-Modal Satellite Active Fire Measurements and Terrain Height

Increasing wildfire occurrence has spurred growing interest in wildfire spread prediction. However, even the most complex wildfire models diverge from observed progression during multi-day simulations, motivating need for data assimilation. A useful approach to assimilating measurement data into complex coupled atmosphere-wildfire models is to estimate wildfire progression from measurements and use this progression to develop a matching atmospheric state. In this study, an approach is developed for estimating fire progression from VIIRS active fire measurements, GOES-derived ignition times, and terrain height data. A conditional Generative Adversarial Network is trained with simulations of historic wildfires from the atmosphere-wildfire model WRF-SFIRE, thus allowing incorporation of WRF-SFIRE physics into estimates. Fire progression is succinctly represented by fire arrival time, and measurements for training are obtained by applying an approximate observation operator to WRF-SFIRE solutions, eliminating need for satellite data during training. The model is trained on tuples of fire arrival times, measurements, and terrain, and once trained leverages measurements of real fires and corresponding terrain data to generate samples of fire arrival times. The approach is validated on five Pacific US wildfires, with results compared against high-resolution perimeters measured via aircraft, finding an average Sorensen-Dice coefficient of 0.81. The influence of terrain height on the arrival time inference is also evaluated and it is observed that terrain has minimal influence when the inference is conditioned on satellite measurements.

SRViT: Vision Transformers for Estimating Radar Reflectivity from Satellite Observations at Scale

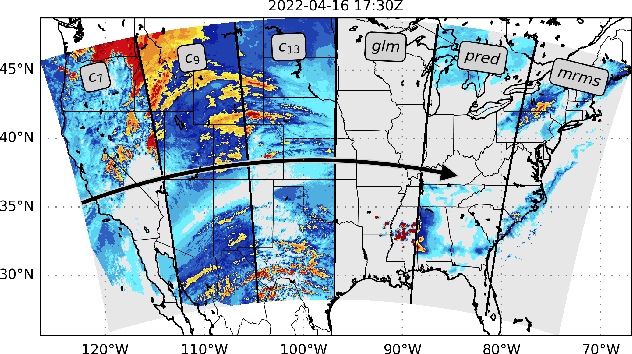
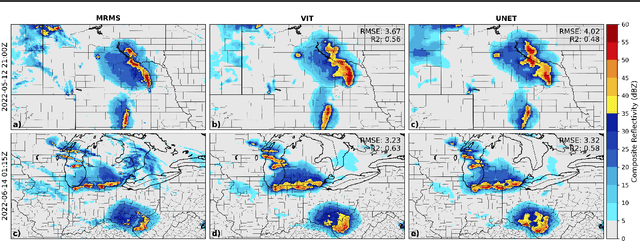
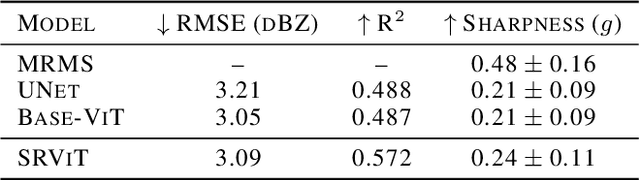
We introduce a transformer-based neural network to generate high-resolution (3km) synthetic radar reflectivity fields at scale from geostationary satellite imagery. This work aims to enhance short-term convective-scale forecasts of high-impact weather events and aid in data assimilation for numerical weather prediction over the United States. Compared to convolutional approaches, which have limited receptive fields, our results show improved sharpness and higher accuracy across various composite reflectivity thresholds. Additional case studies over specific atmospheric phenomena support our quantitative findings, while a novel attribution method is introduced to guide domain experts in understanding model outputs.

Generative Algorithms for Fusion of Physics-Based Wildfire Spread Models with Satellite Data for Initializing Wildfire Forecasts

Increases in wildfire activity and the resulting impacts have prompted the development of high-resolution wildfire behavior models for forecasting fire spread. Recent progress in using satellites to detect fire locations further provides the opportunity to use measurements to improve fire spread forecasts from numerical models through data assimilation. This work develops a method for inferring the history of a wildfire from satellite measurements, providing the necessary information to initialize coupled atmosphere-wildfire models from a measured wildfire state in a physics-informed approach. The fire arrival time, which is the time the fire reaches a given spatial location, acts as a succinct representation of the history of a wildfire. In this work, a conditional Wasserstein Generative Adversarial Network (cWGAN), trained with WRF-SFIRE simulations, is used to infer the fire arrival time from satellite active fire data. The cWGAN is used to produce samples of likely fire arrival times from the conditional distribution of arrival times given satellite active fire detections. Samples produced by the cWGAN are further used to assess the uncertainty of predictions. The cWGAN is tested on four California wildfires occurring between 2020 and 2022, and predictions for fire extent are compared against high resolution airborne infrared measurements. Further, the predicted ignition times are compared with reported ignition times. An average Sorensen's coefficient of 0.81 for the fire perimeters and an average ignition time error of 32 minutes suggest that the method is highly accurate.

CIRA Guide to Custom Loss Functions for Neural Networks in Environmental Sciences -- Version 1

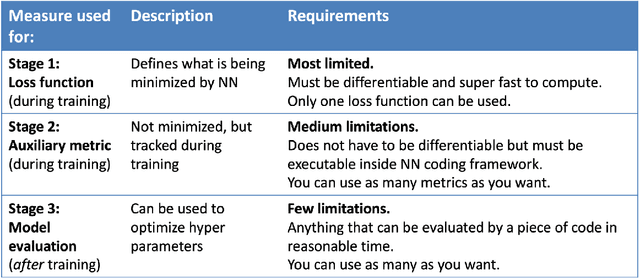
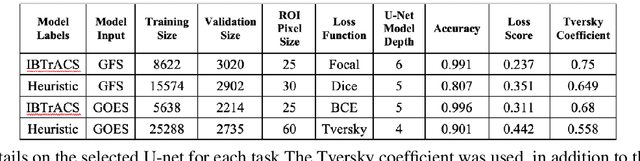
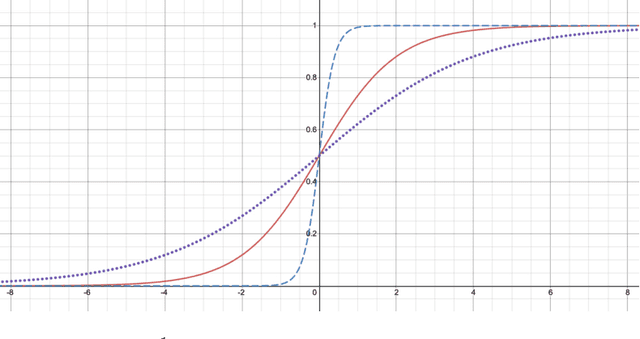
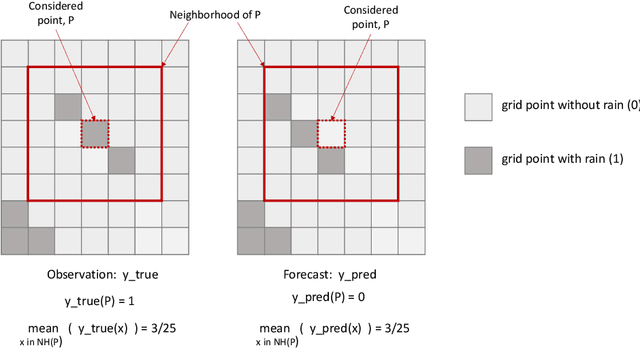
Neural networks are increasingly used in environmental science applications. Furthermore, neural network models are trained by minimizing a loss function, and it is crucial to choose the loss function very carefully for environmental science applications, as it determines what exactly is being optimized. Standard loss functions do not cover all the needs of the environmental sciences, which makes it important for scientists to be able to develop their own custom loss functions so that they can implement many of the classic performance measures already developed in environmental science, including measures developed for spatial model verification. However, there are very few resources available that cover the basics of custom loss function development comprehensively, and to the best of our knowledge none that focus on the needs of environmental scientists. This document seeks to fill this gap by providing a guide on how to write custom loss functions targeted toward environmental science applications. Topics include the basics of writing custom loss functions, common pitfalls, functions to use in loss functions, examples such as fractions skill score as loss function, how to incorporate physical constraints, discrete and soft discretization, and concepts such as focal, robust, and adaptive loss. While examples are currently provided in this guide for Python with Keras and the TensorFlow backend, the basic concepts also apply to other environments, such as Python with PyTorch. Similarly, while the sample loss functions provided here are from meteorology, these are just examples of how to create custom loss functions. Other fields in the environmental sciences have very similar needs for custom loss functions, e.g., for evaluating spatial forecasts effectively, and the concepts discussed here can be applied there as well. All code samples are provided in a GitHub repository.