On Time-optimal Trajectories for a Car-like Robot with One Trailer
Paper and Code
Jan 28, 2013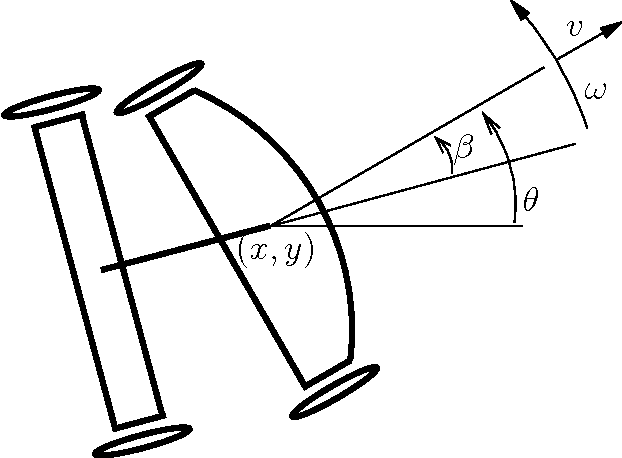



In addition to the theoretical value of challenging optimal control problmes, recent progress in autonomous vehicles mandates further research in optimal motion planning for wheeled vehicles. Since current numerical optimal control techniques suffer from either the curse of dimens ionality, e.g. the Hamilton-Jacobi-Bellman equation, or the curse of complexity, e.g. pseudospectral optimal control and max-plus methods, analytical characterization of geodesics for wheeled vehicles becomes important not only from a theoretical point of view but also from a prac tical one. Such an analytical characterization provides a fast motion planning algorithm that can be used in robust feedback loops. In this work, we use the Pontryagin Maximum Principle to characterize extremal trajectories, i.e. candidate geodesics, for a car-like robot with one trailer. We use time as the distance function. In spite of partial progress, this problem has remained open in the past two decades. Besides straight motion and turn with maximum allowed curvature, we identify planar elastica as the third piece of motion that occurs along our extr emals. We give a detailed characterization of such curves, a special case of which, called \emph{merging curve}, connects maximum curvature turns to straight line segments. The structure of extremals in our case is revealed through analytical integration of the system and adjoint equations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge