Out-of-distribution detection using normalizing flows on the data manifold

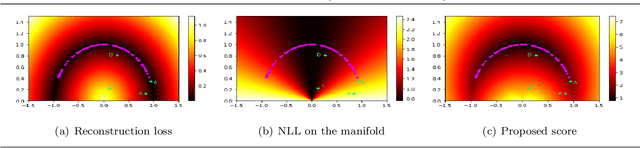
A common approach for out-of-distribution detection involves estimating an underlying data distribution, which assigns a lower likelihood value to out-of-distribution data. Normalizing flows are likelihood-based generative models providing a tractable density estimation via dimension-preserving invertible transformations. Conventional normalizing flows are prone to fail in out-of-distribution detection, because of the well-known curse of dimensionality problem of the likelihood-based models. According to the manifold hypothesis, real-world data often lie on a low-dimensional manifold. This study investigates the effect of manifold learning using normalizing flows on out-of-distribution detection. We proceed by estimating the density on a low-dimensional manifold, coupled with measuring the distance from the manifold, as criteria for out-of-distribution detection. However, individually, each of them is insufficient for this task. The extensive experimental results show that manifold learning improves the out-of-distribution detection ability of a class of likelihood-based models known as normalizing flows. This improvement is achieved without modifying the model structure or using auxiliary out-of-distribution data during training.

Joint Manifold Learning and Density Estimation Using Normalizing Flows

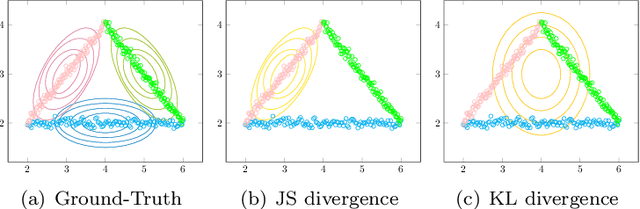
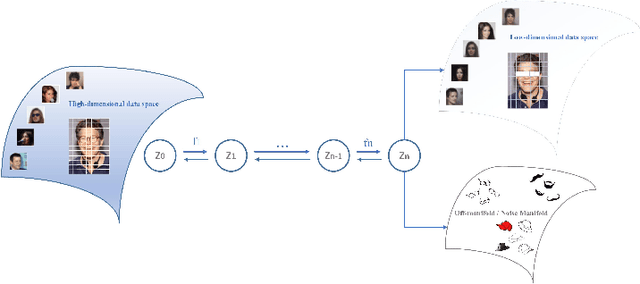
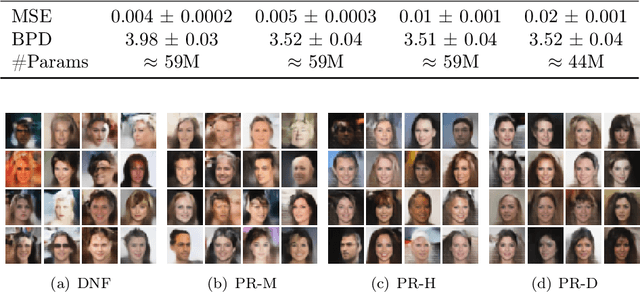
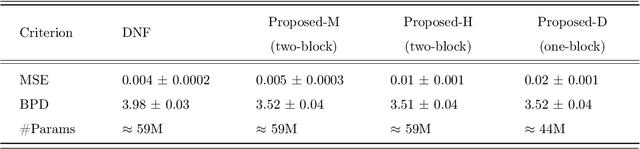
Based on the manifold hypothesis, real-world data often lie on a low-dimensional manifold, while normalizing flows as a likelihood-based generative model are incapable of finding this manifold due to their structural constraints. So, one interesting question arises: $\textit{"Can we find sub-manifold(s) of data in normalizing flows and estimate the density of the data on the sub-manifold(s)?"}$. In this paper, we introduce two approaches, namely per-pixel penalized log-likelihood and hierarchical training, to answer the mentioned question. We propose a single-step method for joint manifold learning and density estimation by disentangling the transformed space obtained by normalizing flows to manifold and off-manifold parts. This is done by a per-pixel penalized likelihood function for learning a sub-manifold of the data. Normalizing flows assume the transformed data is Gaussianizationed, but this imposed assumption is not necessarily true, especially in high dimensions. To tackle this problem, a hierarchical training approach is employed to improve the density estimation on the sub-manifold. The results validate the superiority of the proposed methods in simultaneous manifold learning and density estimation using normalizing flows in terms of generated image quality and likelihood.

A Framework for Multi-View Classification of Features

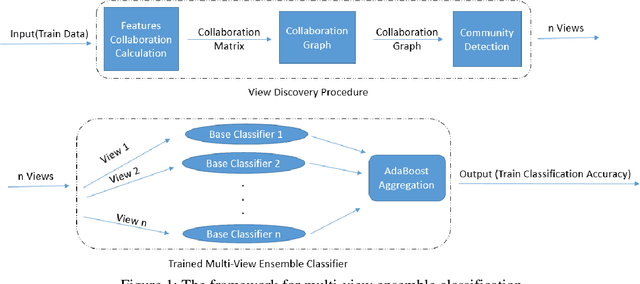
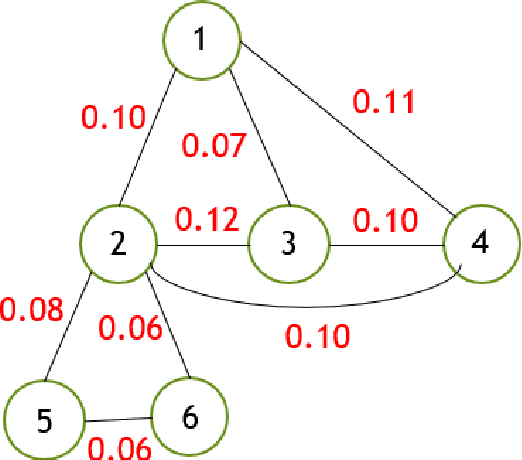
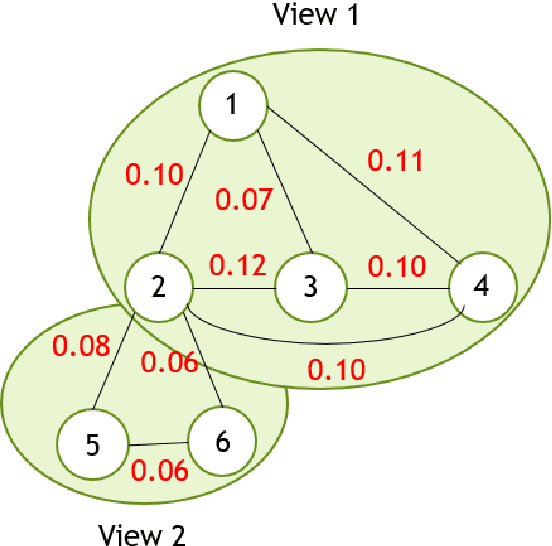
One of the most important problems in the field of pattern recognition is data classification. Due to the increasing development of technologies introduced in the field of data classification, some of the solutions are still open and need more research. One of the challenging problems in this area is the curse of dimensionality of the feature set of the data classification problem. In solving the data classification problems, when the feature set is too large, typical approaches will not be able to solve the problem. In this case, an approach can be used to partition the feature set into multiple feature sub-sets so that the data classification problem is solved for each of the feature subsets and finally using the ensemble classification, the classification is applied to the entire feature set. In the above-mentioned approach, the partitioning of feature set into feature sub-sets is still an interesting area in the literature of this field. In this research, an innovative framework for multi-view ensemble classification, inspired by the problem of object recognition in the multiple views theory of humans, is proposed. In this method, at first, the collaboration values between the features is calculated using a criterion called the features collaboration criterion. Then, the collaboration graph is formed based on the calculated collaboration values. In the next step, using the community detection method, graph communities are found. The communities are considered as the problem views and the different base classifiers are trained for different views using the views corresponding training data. The multi-view ensemble classifier is then formed by a combination of base classifiers based on the AdaBoost algorithm. The simulation results of the proposed method on the real and synthetic datasets show that the proposed method increases the classification accuracy.

Structure Learning of Sparse GGMs over Multiple Access Networks

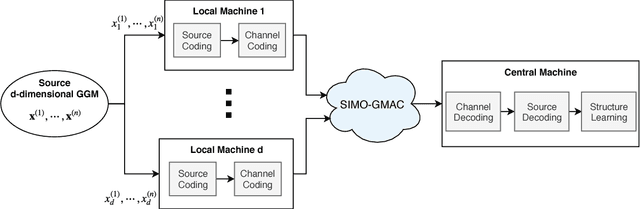
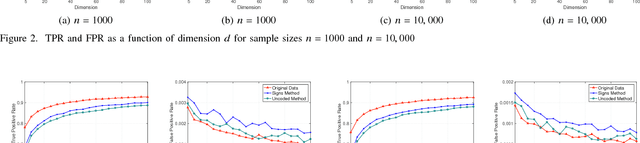
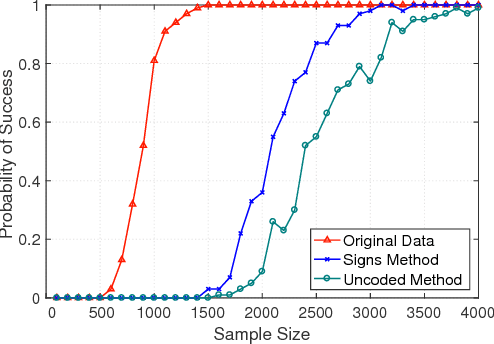
A central machine is interested in estimating the underlying structure of a sparse Gaussian Graphical Model (GGM) from datasets distributed across multiple local machines. The local machines can communicate with the central machine through a wireless multiple access channel. In this paper, we are interested in designing effective strategies where reliable learning is feasible under power and bandwidth limitations. Two approaches are proposed: Signs and Uncoded methods. In Signs method, the local machines quantize their data into binary vectors and an optimal channel coding scheme is used to reliably send the vectors to the central machine where the structure is learned from the received data. In Uncoded method, data symbols are scaled and transmitted through the channel. The central machine uses the received noisy symbols to recover the structure. Theoretical results show that both methods can recover the structure with high probability for large enough sample size. Experimental results indicate the superiority of Signs method over Uncoded method under several circumstances.

Learning of Tree-Structured Gaussian Graphical Models on Distributed Data under Communication Constraints

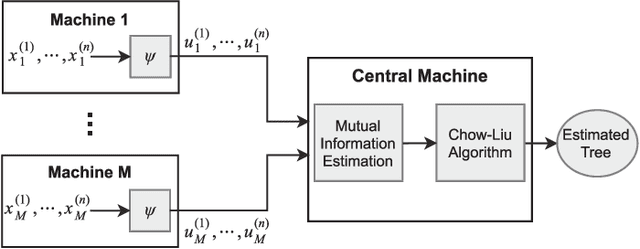
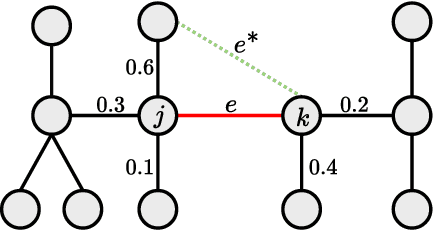
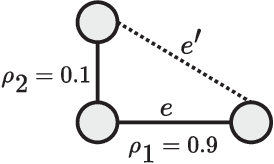
In this paper, learning of tree-structured Gaussian graphical models from distributed data is addressed. In our model, samples are stored in a set of distributed machines where each machine has access to only a subset of features. A central machine is then responsible for learning the structure based on received messages from the other nodes. We present a set of communication efficient strategies, which are theoretically proved to convey sufficient information for reliable learning of the structure. In particular, our analyses show that even if each machine sends only the signs of its local data samples to the central node, the tree structure can still be recovered with high accuracy. Our simulation results on both synthetic and real-world datasets show that our strategies achieve a desired accuracy in inferring the underlying structure, while spending a small budget on communication.

Learning of Gaussian Processes in Distributed and Communication Limited Systems

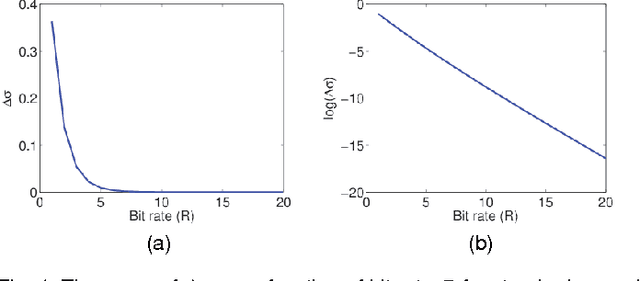
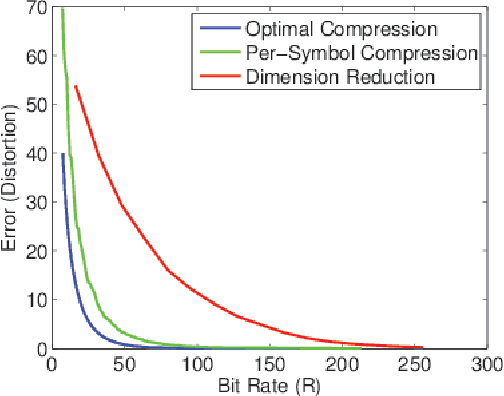
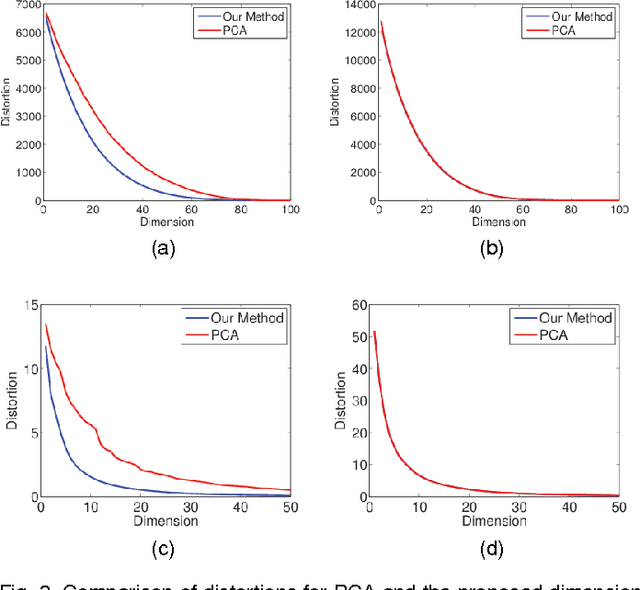
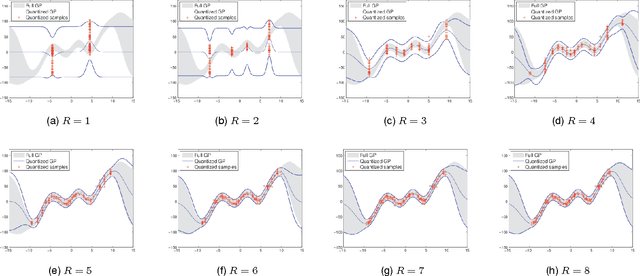
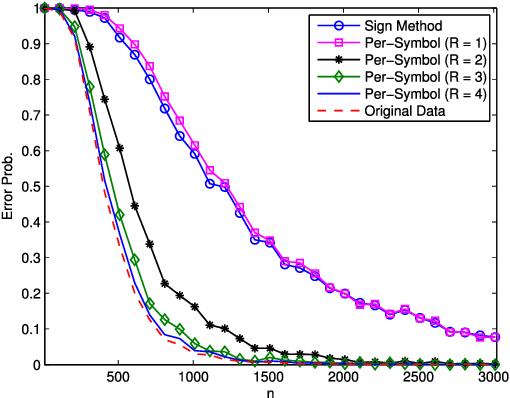
It is of fundamental importance to find algorithms obtaining optimal performance for learning of statistical models in distributed and communication limited systems. Aiming at characterizing the optimal strategies, we consider learning of Gaussian Processes (GPs) in distributed systems as a pivotal example. We first address a very basic problem: how many bits are required to estimate the inner-products of Gaussian vectors across distributed machines? Using information theoretic bounds, we obtain an optimal solution for the problem which is based on vector quantization. Two suboptimal and more practical schemes are also presented as substitute for the vector quantization scheme. In particular, it is shown that the performance of one of the practical schemes which is called per-symbol quantization is very close to the optimal one. Schemes provided for the inner-product calculations are incorporated into our proposed distributed learning methods for GPs. Experimental results show that with spending few bits per symbol in our communication scheme, our proposed methods outperform previous zero rate distributed GP learning schemes such as Bayesian Committee Model (BCM) and Product of experts (PoE).